Minimax elv

A minimax elv a döntéselméletben, a játékelméletben és a statisztikában alkalmazott döntési szabály, ami szerint azt a lehetőséget kell választani, ami minimalizálja a maximális veszteséget. Felfogható a minimális nyereség maximalizálásaként is.

Az elmélet megalkotása a kétfős zéróösszegű játékokkal kezdődött, ami magába foglalta a két játékos szimultán döntéseit és a felváltva tett lépéseit is, aztán bonyolultabb esetekre is kiterjesztették.

A játékelméletben

A minimax elv egy kevert stratégia, ami része a zéró összegű játékok megoldásának. A zéró összegű játékokban a minimax elv megadja a nyeregpontot.

Definíció: Legyen A és B nem üres halmaz, $f:A\times B\to \mathbb {R}$ adott függvény. Az $(x_{0},y_{0})$ pont nyeregpont, ha minden $x\in A$-ra és minden $y\in B$-re $f(x,y_{0})\leq f(x_{0},y_{0})\leq f(x_{0},y).$

Neumann-tétel: Minden olyan kétszemélyes, zéró összegű játéknak van nyeregpontja, amiben véges sok elemi stratégia van. Azaz a legjobb kevert stratégiával az első játékos várható nyereségének maximuma egyenlő a második játékos várható veszteségének minimumával.

Neumann János szerint nem érdemes játékelméletet csinálni a minimax tételnek is nevezett tétel nélkül.

A tétel általánosításai Sion minimaxtétele és Parthasarathy tétele.

Neumann-tétel

Definíció: Egy vektor tetején a vektor legnagyobb koordinátáját értjük; a vektor alja a legkisebb koordinátája.

Neumann-tétel: Minden olyan kétszemélyes, zéró összegű játéknak van nyeregpontja, amiben véges sok elemi stratégia van. Azaz a legjobb kevert stratégiával az első játékos várható nyereségének maximuma egyenlő a második játékos várható veszteségének minimumával.

A tétel egy másik alakban: Jelölje A a játék kifizetési mátrixát. Az A oszlopai által feszített politópban levő elemek minimuma egyenlő az A sorai által feszített politópban levő elemek aljának minimumával.

Bizonyítás: a dualitástétel segítségével.

A dualitástétel alkalmazásában a primál feladat: keresünk minimális w-t, amihez van $x\geq 0,$ $ex=1,$ $Ax\leq we,$ ahol $e$ azt a vektort jelöli, aminek minden koordinátája 1. Ez megfelel a $\min\{$ $w:-Ax+we\geq 0,$ $x\geq 0,$ $ex=1\}$ lineáris programnak.

A duál feladat: keresünk maximális z-t, amihez van $ey=1,$ $yA\geq ze.$ Ez megfelel a $\max\{$ $z:y(-A)+ze\leq 0,$ $y\geq 0,$ $ey=1\}$ lineáris programnak.

Maximin

Sokszor előfordul a játékelméletben, hogy a maximin különbözik a minimaxtól. A zéró összegű játékok elméletében a minimax az ellenfél nyereségének minimalizálását jelöli, ami a zéró összegű játékok esetén a saját veszteség minimalizálásának, azaz a saját nyereség maximalizálásának felel meg.

A maximin a nem zéró összegű játékok esetén használatos stratégiát jelenti, ami maximalizálja a saját nyereséget. Ez általában nem egyezik az ellenfél nyereségének a minimumával, vagy a nyeregponti stratégiával.

Példa

	B1	B2	B3
A1	+3	−2	+2
A2	−1	0	+4
A3	−4	−3	+1

A következő példa egy zéró összegű játék. A két játékos, A és B szimultán lép.

Tegyük fel, hogy a játék kifizetési mátrixa az A játékos számára a fenti mátrix, és a B játékos számára az előjelek fordítottak. Ekkor A minimax választása A2, mivel itt a legrosszabb esetben 1-et kell fizetni, és B minimax választása B2, mert ekkor a legrosszabb esetben nincs nyeremény.

Ez a megoldás nem stabil. Ha B azt hiszi, hogy A A2-t választja, akkor B1 mellett dönt. Ha A azt hiszi, hogy B B1 mellett dönt, akkor megjátssza A1-et. Ha B azt hiszi, hogy A A1-et játssza meg, akkor B2-t választja. A determinisztikus stratégia kiismerhető, ezért csak nem determinisztikus stratégia lehet stabil.

A stabil kevert stratégiák: A 1/6 valószínűséggel választja A1-et, és 5/6 valószínűséggel A2-t. B 1/3 valószínűséggel választja B1-et, és 2/3 valószínűséggel B2-t. Ezek a stratégiák stabilak, és nem javíthatók.

A minimax elv korlátai

A minimax elv nem mindig vezet mindkét fél számára optimális megoldáshoz. Erre példa a fogolydilemma.

A klasszikus fogolydilemmában a kifizetési mátrix:

	Egyik tagad	Egyik vall
Másik tagad	Mindketten 6 hónapot kapnak	Egyik szabad, másik 10 évet kap
Másik vall	Egyik 10 évet kap, másik szabad	Mindkettő 6 évet kap

Ha mindkét fogoly abszolút önző és egyetlen céljuk saját büntetésük minimalizálása, akkor mindkét fogoly vallani fog, és mindketten 6 év börtönt kapnak, pedig a kooperáció lenne a legjobb stratégia.

Kombinatorikus játékelmélet

A kombinatorikus játékelméletben a minimax a következő lépésekre vezet:

Az egyszerű változatban minden játékos nyerhet, veszíthet, vagy döntetlent érhet el, mint a tic-tac-toe-ban. Ez az amőba egy háromszor hármas táblán játszott változata, ahol a cél három jel elhelyezése egy sorban, oszlopban, vagy átlón.

Ha az A játékos egy lépéssel nyerhet, akkor a legjobb lépése a nyerő lépés. Ha a B játékos tudja, hogy az egyik lépése után A nyerhet, viszont egy másik lépése után legfeljebb döntetlent érhet el, akkor az utóbbit választja.

A játék folyamán mindig látható, hogy mi a legjobb lépés. A minimax algoritmus segít megtalálni ezt. Módszere a játék elemzése az utolsó, nyerő lépéstől a kezdőlépésig. Felteszi, hogy A minden lépésben maximalizálni akarja A nyerési esélyeit, míg B csökkenteni igyekszik azokat, ezzel próbálva növelni saját esélyeit a győzelemre.

Minimax algoritmus váltakozó lépéses játékokra

Rekurzív algoritmus a következő lépés meghatározására. A játékosok száma n, de többnyire kettő. A játék minden állásához tartozik egy érték, ami a heurisztikus kiértékelő függvény segítségével számítható. Ez jelzi, hogy mennyire kedvez egy játékosnak az az állás. A soron következő játékos maximalizálja az ellenfelek lépései után elérhető minimális értéket.

Az egyik módszer a biztos győzelmet +1 nyereségnek tekinti. Egy másik módszer szerint egy nyerő lépés nyeresége végtelen. A játékot A szempontjából tekintve A a maximalizáló, és B a minimalizáló játékos. A fenti algoritmus minden álláshoz plusz vagy mínusz végtelent rendel, mert minden állás a végső állás értékét veszi fel. Gyakran ez csak a játék vége után lehetséges, mert a számítógépes kapacitás nem elegendő a teljes játék áttekintésére. Ilyen például a sakk és a go. Csak a végjátékot lehet így végigelemezni, így az egyes állásokhoz véges értékeket rendelnek, amik a nyerés bizonyosságát fejezik ki az egyik vagy a másik játékos számára.

Ez a módszer kiterjeszthető egy heurisztikus kiértékelő függvény segítségével, ami anélkül rendel véges értékeket az egyes állásokhoz, hogy áttekintené az összes lehetséges befejezést. Ehelyett csak bizonyos számú lépést elemez ki előre. A Deep Blue például 12 lépést tud átlátni, és erre alkalmazni a heurisztikus kiértékelő függvényt.

Az algoritmus a játékfa csúcsainak felkutatásaként képzelhető el. Az egy állásban megtehető lépések átlagos száma jó elágazási tényező. A csúcsok száma rendszerint exponenciálisan nő, ezért nem hatékony a teljes játék végigelemzéséhez.

A naiv minimax algoritmus hatékonysága nagymértékben javítható az alfa-béta vágással. Más heurisztikus metszési módszereket is használnak, de ezek nem tudják garantálni az eredményt.

Az alfa-béta vágás nem értékel ki teljesen olyan állásokat, amikről bebizonyosodott, hogy rosszabbak egy korábban vizsgált állásnál.

A minimax algoritmus pszeudokódja

A minimax algoritmus pszeudokódja itt látható:

function minimax(csúcs, mélység)
    if a csúcs levél, or mélység = 0
        return a csúcs heurisztikus értéke
     else
        let α := -∞
        foreach gyerekére a csúcsnak
                      { a kiértékelés mindkét játékos számára ugyanaz }
            let α := max(α, -minimax(gyerek, mélység-1))
        return α

A kód felhasználja azt a megfigyelést, hogy $\max(a,b)=-\min(-a,-b)$, így egységesen tudja kezelni a két játékost.

Példa

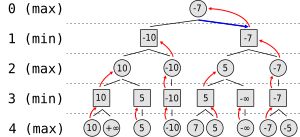
Tegyük fel, hogy egy játékban minden lépésben csak két választási lehetőség van. Az algoritmus a jobboldalt látható fát generálja. A fában a körök jelzik a maximalizáló játékost, és a négyzetek a minimalizálót. A számításigény miatt a fát négy lépésre korlátozzuk.

Az algoritmus a levelektől kezdve minden levelet kiértékel a heurisztikus értékelőfüggvény szerint, és a fenti értékeket adja. Azt, hogy maximalizáló játékos nyer, plusz végtelen jelöli, és mínusz végtelen látható, ha a minimalizáló játékos nyer. A harmadik szinten az algoritmus a gyerekek minimumát választja, és ezt írja a megfelelő csúcsba. A következő lépésben a harmadik szint maximális értékei kerülnek a második szintre. Az algoritmus felváltva veszi a maximumokat és a minimumokat, amíg a gyökérhez nem ér. Ott a nagyobb értéket választja (az ábrán kék nyíl jelöli). Ezt kell lépnie a játékosnak, hogy minimalizálja a maximális veszteséget.

Statisztikai döntéselmélet

Legyen $\vartheta \in \Theta$ paraméter, és legyen a $\vartheta$ paraméter becslése $\delta$. Jelölje $R(\theta ,\delta )$ a rizikófüggvényt, ami rendszerint a veszteségfüggvény integrálja. A ${\tilde {\delta }}$ becslés minimax, ha

$\sup _{\theta }R(\theta ,{\tilde {\delta }})=\inf _{\delta }\sup _{\theta }R(\theta ,\delta ).$

A döntéselmélet egy alternatív elmélete a Bayes-becslés használatán alapul, ami a $\Pi$ a becsülni kívánt paraméter feltételezett a priori eloszlásának ismeretében az a posteriori rizikót:

$\int _{\Theta }R(\theta ,\delta )\,d\Pi (\theta ).$

A bizonytalansággal szemben

A minimaxról szóló elméletet arra az esetre is kiterjesztették, amikor egy játékos van, de a döntések eredményei ismeretlen tényeken múlnak. Például az ásványok keresése lehet, hogy nagy veszteséggel jár, mert nincsenek ásványok, de lehet, hogy nagy nyereséget okoz, mert sok és értékes ásvány található.

Egy másik megközelítés szerint ez a természet elleni játék, és Murphy törvényeihez hasonló elgondolással minimalizálja a várható veszteség maximumát a két játékosú zéró összegű játékoknál használt algoritmussal.

Források

• Frank András: Operációkutatás [1] pdf
• Illés Tibor: Játékelmélet
• Mérő László: Mindenki másként egyforma
• A zéró összegű játékok minimax elemzése
• Bemutató applet
• "Maximin principle" a Dictionary of Philosophical Terms and Names című könyvből.
• Play a betting-and-bluffing game against a mixed minimax strategy
• A The Dictionary of Algorithms and Data Structures minimax cikke
• A minimax algoritmus megjelenítése játékfával (Java applet)
• CLISP minimax - játék.