Bézier-görbe

A Bézier-görbe a számítógépes grafikában gyakran használt parametrikus görbe. A Bézier-görbe több dimenzióra való általánosítását Bézier-felületnek nevezik, ezeknek speciális esete a Bézier-háromszög.
A vektorgrafikában a Bézier-görbéket szabadon alakítható sima görbék modellezésére használják. A képszerkesztő programok, mint például az Inkscape, Adobe Photoshop vagy a GIMP a görbe vonalak rajzolásához egymáshoz kapcsolt Bézier-görbék sorozatát használják. Ezeket a görbéket nem korlátozza a raszterképek felbontása és interaktívan alakíthatóak. A Bézier-görbéket a számítógépes animációban a mozgások vezérlésének eszközeként is használják olyan programok, mint például az Adobe Flash, Adobe After Effects, Microsoft Expression Blend, Blender, Maya és az Autodesk 3D Studio Max.
A Bézier-görbéket az idő dimenziójában is használják, különösen az animációkban és az interfésztervezésben, azaz Bézier-görbéket lehet használni a képernyőn végbemenő mozgások sebességének az idő függvényében való megadására ahelyett, hogy fázisképenként egyszerűen néhány képpontnyi elmozdulást írnának elő.
A Bézier-görbék a matematikában jóval a számítógépek illetve számítógépes grafika megjelenése előtt ismertek voltak. Szergej Natanovics Bernstein orosz matematikus 1912-ben publikált cikkében a Hermite-polinomokkal kapcsolatos kutatásai során definiálja a később róla elnevezett Bernstein-polinomot. Ezt a x ∈ [0, 1] intervallumra korlátozott Bernstein-polinomot használta fel Pierre Bézier a Renault gyár mérnöke a számítógépes grafikai tervezésben.[1]
A Bézier-görbékről 1962-ben Pierre Bézier francia mérnök sok publikációja jelent meg, aki a gépkocsi-karosszériák tervezésénél használta azokat. A görbék számítógépes grafikai alkalmazásához szükséges számítógépes algoritmust 1959-ben Paul de Casteljau dolgozta ki. Ez a Bézier-görbék előállításának egy numerikusan stabil módszere: a róla elnevezett de Casteljau-algoritmus.
Alkalmazás
[szerkesztés]Számítógépes grafika
[szerkesztés]A Bézier-görbéket széles körben alkalmazzák a számítógépes grafikában sima görbe vonalak modellezésére. A görbék interaktív módszerrel is könnyen igazíthatók kontrollpontjaik mozgatásával. Affin transzformációjuk, mint például a transzláció és a rotáció, könnyen elvégezhető kontrollpontjaik megfelelő transzformációjával.
Általában másod- és harmadfokú Bézier-görbéket használnak; a magasabb fokszámú görbék előállítása túlságosan sok számítást igényel. A bonyolultabb alakú vonalak közelítő alakját alacsonyabb fokszámú Bézier-görbékből állítják össze. A csatlakozási pontokon a görbe simaságát az biztosítja, ha a közös pont és a hozzájuk közelebb eső kontrollpontok egy egyenesen fekszenek.
A Bézier-görbe raszterré alakításának legegyszerűbb módja az, ha sok közel fekvő pontját meghatározzák, majd ezeket közelítő egyenesekkel összekötik. Ennek a módszernek a hibája, hogy nem biztosítható, hogy a raszterkép mindenütt elegendően simának látszódjék, ha a pontok túlságosan távol helyezkedhetnek el egymástól. Emiatt sokszor túlságosan sok pontot generál az ilyen algoritmus az egyeneshez közel álló görbék esetében. Szokásos módszer a rekurzív felosztásos eljárás, melynek során az algoritmus ellenőrző pontokat vizsgál meg, hogy a közelítő egyeneshez eléggé közel fekszenek-e, és ha nem, a két pont között további pontot jelöl ki, majd megismétli az eljárást.
Animáció
[szerkesztés]Animációnál a Bézier-görbéket például mozgások leírására használják. A felhasználó kijelöli a kívánt útvonalat, az alkalmazás pedig előállítja az objektum mozgásának megfelelő képkockákat. A módszer térbeli mozgásokra is alkalmazható.
Betűk
[szerkesztés]A TrueType betűkészlet másodfokú Bézier-görbékből összeállított Bézier-splineokat használ a betűk megjelenítéséhez.
A korszerű képmegjelenítő rendszerek, mint a PostScript, Asymptote és a Metafont harmadfokú Bézier-görbékből álló Bézier-splineokkal rajzolja fel a betűket.
Különböző fokszámú görbék
[szerkesztés]Lineáris Bézier-görbe
[szerkesztés]Adott a P0 és P1 pont, a lineáris Bézier-görbe egyszerűen a két pontot összekötő egyenes szakasz. A görbét a
függvény írja le, és ekvivalens a lineáris interpolációval.
Másodfokú Bézier-görbe
[szerkesztés]A másodfokú Bézier-görbét három pont: a P0, P1, és P2 határoz meg, és a B(t) függvény írja le:
A görbe a P0 ponttól indul a P1 pont irányába, majd elhajlik, és a P2 pontban végződik. Más szavakkal mind a P0, mind a P2 pont érintője átmegy a P1 ponton. Ez közvetlenül látható a Bézier-görbét leíró függvény deriváltjából:
A másodfokú Bézier-görbe egyben egy parabolaív is.
Harmadfokú Bézier-görbe
[szerkesztés]A harmadfokú Bézier-görbét (egy síkban fekvő vagy térbeli elhelyezkedésű) négy pont: P0, P1, P2 és P3 definiál. A görbe a P0 pontból indul a P1 irányába és a P3 pontba érkezik a P2 irányából. Általában nem halad át a P1 vagy P2 ponton, ezek csak az irányokról adnak információt. A P0 és P1 pont közötti távolság azt határozza meg, hogy „milyen hosszan” halad a P2 irányába, mielőtt a P3 pont felé fordul. A görbe parametrikus egyenlete:
A P1 és P2 bizonyos elhelyezkedése önmagát metsző vagy csúcsos görbét eredményezhet.
Általánosítás
[szerkesztés]Az n-edfokú Bézier-görbe a következőképpen általánosítható. Legyen n+1 pont: P0, P1,..., Pn, a Bézier-görbe egyenlete:
ahol a binomiális együttható.
Például n = 5 esetre:
Ez az összefüggés az alábbi rekurzív formulával fejezhető ki: Jelölje a P0, P1, ..., Pn pontokkal meghatározott Bézier-görbét. Ezzel
Más szavakkal az n-edfokú Bézier-görbe két (n – 1)-edfokú Bézier-görbe közötti lineáris interpoláció.
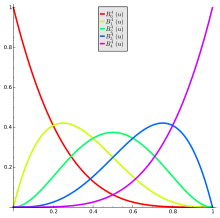
Tulajdonságai
[szerkesztés]A parametrikus görbékhez néhány fogalom kapcsolódik. A Bézier-görbe egyenlete
ahol a
polinomok az úgynevezett n-edfokú Bernstein polinomok, ahol t0 = 1 és (1 – t)0 = 1.
Az binomiális együttható alternatív jelölése
A Pi pontokat a Bézier-görbéhez tartozó kontrollpontoknak hívják. A görbéhez tartozó keret a kontrollpontok egyenesekkel való összekötésével kialakított tört vonalsorozat.
- A görbe a P0 pontnál kezdődik és a Pn pontnál ér véget. Ezt a módszert végpont interpolációnak hívják.
- A görbe akkor és csakis akkor egyenes vonal, ha a kontrollpontok egy egyenesen fekszenek.
- A görbe kezdőpontjának (végpontjának) érintője a keret első (utolsó) szakasza.
- A görbét bármely pontjánál két részgörbére lehet vágni, mindkettő szintén Bézier-görbe.
- Néhány egyszerűnek látszó görbe (például a kör) nem helyettesíthető pontosan Bézier-görbével vagy szakaszaival, bár négy harmadfokú Bézier-görbével közelített kör a pontos alakzattól mindössze egy ezredrésznyire tér el a kontrollpontok megfelelő felvételével.
- Egy Bézier-görbéhez rajzolt egyenközű („párhuzamos”) görbét néhány kivételtől eltekintve nem lehet Bézier-görbével pontosan leírni.
Bézier-görbék szerkesztése
[szerkesztés]![Animation of a linear Bézier curve, t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/00/B%C3%A9zier_1_big.gif/240px-B%C3%A9zier_1_big.gif)
|
| Lineáris Bézier-görbe animációja, 0 ≤ t ≤1 |
Lineáris görbe
[szerkesztés]A t paraméter a lineáris Bézier-görbe esetén szemléletesen a B(t) távolságát jelenti a P0 ponttól a P1 irányában. Például t=0,25 esetén a B(t) a P0 ponttól P1 pontig terjedő távolság negyed részét tette meg. A B(t) egyenest ír le a P0 pont és a P1 pont között.
Másodfokú görbe
[szerkesztés]A másodfokú Bézier-görbéknél a Q0 és Q1 segédpontot a t paraméter függvényében így lehet szerkeszteni: (t 0 és 1 között változik)
- A Q0 pont helyzete P0 ponttól P1 pontig változik, miközben lineáris Bézier-görbét ír le.
- A Q1 pont helyzete P1 ponttól P2 pontig változik, miközben lineáris Bézier-görbét ír le.
- A B(t) pont helyzete Q0 ponttól Q1 pontig változik, miközben másodfokú Bézier-görbét ír le.
 |
![Animation of a quadratic Bézier curve, t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3d/B%C3%A9zier_2_big.gif/240px-B%C3%A9zier_2_big.gif)
| |
| Másodfokú Bézier-görbe szerkesztése | Másodfokú Bézier-görbe animációja, 0 ≤ t ≤ 1 |
Magasabb fokszámú görbék
[szerkesztés]Magasabb fokszámú görbékhez több közbenső pont szükséges. Harmadfokú görbéhez Q0, Q1, és Q2 közbenső pontot lehet szerkeszteni, ezek lineáris Bézier-görbéket határoznak meg, az R0 és R1 pont pedig másodfokú Bézier-görbét ír le:
 |
![Animation of a cubic Bézier curve, t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/db/B%C3%A9zier_3_big.gif/240px-B%C3%A9zier_3_big.gif)
| |
| Harmadfokú Bézier-görbe szerkesztése | Harmadfokú Bézier-görbe animációja, 0 ≤ t ≤ 1 |
Negyedfokú görbéhez a Q0, Q1, Q2 és Q3 pont lineáris, az R0, R1 és R2 pont másodfokú, az S0 és S1 pont pedig harmadfokú Bézier-görbét határoz meg:
 |
![Animation of a quartic Bézier curve, t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/a/a4/B%C3%A9zier_4_big.gif/240px-B%C3%A9zier_4_big.gif)
| |
| Negyedfokú Bézier-görbe szerkesztése | Negyedfokú Bézier-görbe animációja, 0 ≤ t ≤ 1 |
Fokszámemelés
[szerkesztés]Az n-edfokú Bézier-görbét ugyanolyan alakú n + 1 görbévé lehet alakítani. Ez akkor hasznos, ha az adott szoftver csak bizonyos fokszámú Bézier-görbéket támogat. Például rajzolható negyedfokú Bézier-görbe a Cairo programmal is, holott az csak harmadfokú Bézier-görbét használ.
A fokszám emeléshez az egyenletből lehet kiindulni. Minden tagot megszorozva (1 – t) vagy t szorzóval a fokszám eggyel emelkedik. Az alábbi példa a másodfokú görbe harmadfokúvá alakítását mutatja be:
Tetszőleges n fokszámra az alábbiak írhatók:

ahol és tetszőleges.
Az új kontrollpontok:[2]
Racionális Bézier-görbék
[szerkesztés]
A racionális Bézier-görbék további súlyokat adnak a függvényekhez abból a célból, hogy pontosabban közelítsék a kívánt alakot. A számláló súlyozott Bernstein-formájú Bézier-görbe, a nevező pedig Bernstein-polinomok súlyozott összege. A racionális Bézier-görbék többek között kúpszelet szakaszok pontos megjelenítésére használhatók[3]
Legyen n + 1 darab Pi kontrollpont, a racionális Bézier-görbe egyenlete:
vagy egyszerűen
Tudnivalók:
- Bármilyen NURBS görbe hiba nélkül megadható racionális Bézier-görbék seregével is, amik a végpontjaiknál csatlakoznak. (A bizonyításhoz a NURBS csomópontvektorában minden csomópont multiplicitását k-ra kell növelni csomópontbeszúrásokkal, ha k-adfokú a NURBS, és így végül leolvashatóak a k-adfokú Bézier-görbék, amik a kibővített csomópontú NURBS szegmensei lesznek.)
- Ennél több is elmondható: minden k dimenziós C(t) görbe, ami explicit felírható legfeljebb n-edfokú polinomokkal, felírható n-edfokú Bézier- és B-Spline-görbeként is, és minden k dimenziós C(t) görbe, ami felírható legfeljebb n-edfokú polinomok hányadosaival, felírható n-edfokú racionális Bézier-görbeként és NURBS-ként is. Helyesebb tehát a Béziert és a NURBS-ot reprezentációnak hívni, hiszen egy adott görbét több különböző módon is reprezentálhatunk, és kiválaszthatjuk a konkrét alkalmazás szempontjából számunkra legelőnyösebb, legkényelmesebb reprezentációt.
- Racionális Bézier-görbék eltolási görbéje sem adható meg általában hiba nélkül racionális Bézier-görbékkel. Az ok leolvasható az eltolási görbe képletéből. Ha az eltolás értéke d, akkor:
A legnagyobb baj a hányadosban szereplő gyökjellel van, ugyanis ha a gyökvonás nem végezhető el a deriváltak négyzetösszeg-polinomján szimbolikusan, akkor a helyébe írható Taylor-polinom végtelen számú nemnulla tagot fog tartalmazni. Ezt csak egy végtelen fokszámú racionális Bézier-görbével lehetne hibátlanul megadni. Jó megoldás nincs; ilyenkor az eltolási görbe jó közelítéshez vagy egy lényegesen magasabb fokszámú polinom kell (ami általában nem praktikus), vagy a kontrollpontok számát kell az elvárt hiba függvényében exponenciálisan megnövelni.
Jegyzetek
[szerkesztés]- ↑ http://www.ams.org/samplings/feature-column/fcarc-bezier#2 From Bézier to Bernstein
- ↑ Gerald Farin: Curves and surfaces for computer-aided geometric design. Elsevier Science & Technology Books 1997, ISBN 978-0-12-249054-5, 4. kiadás
- ↑ Neil Dodgson: Some Mathematical Elements of Graphics: Rational B-splines
Fordítás
[szerkesztés]- Ez a szócikk részben vagy egészben a Bézier curve című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Külső hivatkozások
[szerkesztés]- Kovács Zoltán: Számítógépi geometria. 3. fejezet Archiválva 2016. március 13-i dátummal a Wayback Machine-ben
- Java applet
- Poly Bézier Curve Construction by jsDraw2D Graphics Library. The library is for JavaScript and is open source. The drawPolyBezier function in jsDraw2D implements the poly Bézier drawing algorithm.
- Don Lancaster's Cubic Spline Library describes how to approximate a circle (or a circular arc, or a hyperbola) by a Bézier curve; using cubic splines for image interpolation, and an explanation of the math behind these curves.
- Weisstein, Eric W.: Bézier Curve (angol nyelven). Wolfram MathWorld
- Module for Bézier Curves by John H. Mathews
- Multi-degree 2D Bézier Curve java applet Archiválva 2011. június 7-i dátummal a Wayback Machine-ben - An interactive bezier curve applet implementing: adding and deleting control points, showing control polygon and convex hull, manipulating sampling amount and elevating degree without changing the curve.
- PolyBezier – The Microsoft Win32 GDI API function, which draws Bézier curves in Windows graphic applications, like MS Paint.
- Finding All Intersections of Two Bézier Curves. – Locating all the intersections between two Bézier curves is a difficult general problem, because of the variety of degenerate cases. By Richard J. Kinch.
- SketchPad – A small program written in C and Win32 that implements the functionality to create and edit Bézier curves. Demonstrates also the use of de Casteljau's algorithm to split a Bézier curve.
- Bézier Curves interactive demo using ActionScript and FlashPlayer Archiválva 2009. április 23-i dátummal a Wayback Machine-ben – Includes Bézier curve and additional drawing/text tools.
- Drawing Cubic Bézier Curves explained by using Flash Actionscript Archiválva 2011. május 15-i dátummal a Wayback Machine-ben
- 3rd order Bézier Curves applet
- Living Math Bézier applet
- Living Math Bézier applets of different spline types, Java programming of splines in An Interactive Introduction to Splines
- From Bézier to Bernstein Feature Column from American Mathematical Society
- Bézier Curves demo using Flash Actionscript
- Bézier Curves drawer using C/Opengl
- Online experiments with the open source JavaScript library JSXGraph
- A full Bézier Curve Primer with interactive graphics (javascript)

![{\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}+t(\mathbf {P} _{1}-\mathbf {P} _{0})=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}{\mbox{ , }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24758aca60716c16f5c8c48824a5f4bef6cbc19b)
![{\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae58cba03138bd23af7a6f19458bd339011aee2b)

![{\displaystyle \mathbf {B} (t)=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t\mathbf {P} _{1}+3(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{3}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/037aa85c999e3e972d2e0d26926534c78e1aa3e7)
![{\displaystyle {\begin{aligned}\mathbf {B} (t)&=\sum _{i=0}^{n}{n \choose i}(1-t)^{n-i}t^{i}\mathbf {P} _{i}\\&=(1-t)^{n}\mathbf {P} _{0}+{n \choose 1}(1-t)^{n-1}t\mathbf {P} _{1}+\cdots \\&{}\quad \cdots +{n \choose n-1}(1-t)t^{n-1}\mathbf {P} _{n-1}+t^{n}\mathbf {P} _{n},\quad t\in [0,1],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88462cebb383fcd2fe166309937bbea60886ba01)

![{\displaystyle {\begin{aligned}\mathbf {B} (t)&=(1-t)^{5}\mathbf {P} _{0}+5t(1-t)^{4}\mathbf {P} _{1}+10t^{2}(1-t)^{3}\mathbf {P} _{2}\\&{}\quad +10t^{3}(1-t)^{2}\mathbf {P} _{3}+5t^{4}(1-t)\mathbf {P} _{4}+t^{5}\mathbf {P} _{5},\quad t\in [0,1].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b69ea4b14cde2567e52df7c5f3997b61086257c4)


![{\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i},\quad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b386c714e76e16f8c55beffd6c3c0470cd070fd8)














