Arkhimédészi spirál

Egy arkhimédészi spirál egyik ágának három 360°-os fordulata

Arkhimédészi spirál nevezetes tulajdonságai

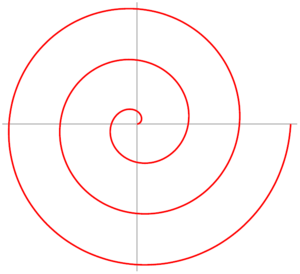
Az arkhimédészi spirál olyan spirális síkgörbe, mely azon pontok mértani helye, melyeket mozgása során pillanatnyilag elfoglal egy rögzített ponttól állandó sebességgel mozgó és ugyanazon rögzített pont körül egyenletes szögsebességgel forgó pont. Ezt az (r, θ) polárkoordinátákkal a következő egyenlet is leírja:

$\,r=a+b\theta$

ahol a és b valós számok. Az a paraméter megváltoztatása elfordítja a pólus körül a görbét, a b paramétertől pedig a sorban következő fordulatok közötti távolság függ.

Arkhimédész ezt a spirálist "A spirálisokról" c. könyvében írta le.

Az arkhimédészi spirálnak két ága van, egyik a θ > 0, másik a θ < 0 tartományra. A két ág simán csatlakozik egymáshoz az origóban (ha a=0, akkor a θ = 0 pontban). A két ág egymásnak tükörképe egy, a póluson átmenő egyenesre, ha a=0, akkor a függőleges egyenesre.

Egy pont polártangensének hossza (polártangens az az egyenes szakasz, melyet a pólustól az $\,r$ sugárra merőleges egyenesen a $\,P$ pont érintője metsz ki: az $\,{\overline {OT}}$ szakasz):

$\,r^{2}b$

A $\,T$ pont Galilei-spirált ír le. A polárszubnormális annak a derékszögű háromszögnek az $\,{\overline {ON}}$ befogója, melyet a sugár, a polártangens és a pontból az érintőre merőleges egyenesek alkotnak. Ennek hossza:

$\,b$,

az érintő és a sugár szöge:

$\,\alpha =\arcsin {\frac {\theta }{\sqrt {1+\theta ^{2}}}}=\arccos {\frac {1}{\sqrt {1+\theta ^{2}}}}$,

Az $\,{\widehat {OP}}$ ívhosszúság a pólus és a $\,\theta$ polárszögű pont között:

$\,s={\frac {b}{2}}(\theta {\sqrt {1+\theta ^{2}}}+\operatorname {arsh} \theta )$

A görbületi sugár:

$\,\rho ={\frac {{(b^{2}+r^{2})}^{3/2}}{2b^{2}+r^{2}}}=b{\frac {{(\theta ^{2}+1)}^{3/2}}{\theta ^{2}+2}}$,

Egyéb spirális síkgörbék

A arkhimédészi spirál elnevezést ritkábban a spirális görbék erre az általánosabb csoportjára is használják:

$r=a+b\theta ^{1\!/\!x}.$

A közönséges arkhimédészi spirál esetén x = 1. Más spirális görbék: a logaritmikus spirál, a hiperbolikus spirál, a parabolikus spirál vagy Fermat-spirál, és a lituus. A természetben előforduló statikus spirális formák legtöbbje nem arkhimédészi, hanem logaritmikus spirál.

Alkalmazás

Arkhimédészi spirál alakú állórésszel és járókerékkel bíró szivattyú elve

Az arkhimédészi spirálisnak igen sok gyakorlati alkalmazása van. Egyes vákuumszivattyúk két egybevágó spirális alakú résszel rendelkeznek. Az egyik rész áll, a másik pedig (a járókerék) forgás nélküli bolygó mozgást végez körülötte, úgy, hogy a két felület szorosan egymáson csúszik, biztosítva ezzel a jó tömítést a nyomócsonk és a szívónyílás között. Ezen az elven folyadékok és gázok szivattyúzására is készítenek eszközöket. A hagyományos hanglemezek barázdája szintén arkhimédészi spirális alakú, ezzel biztosítják, hogy a technikailag lehetséges leghosszabb zenét lehessen rajtuk tárolni.

További információk

• Weisstein, Eric W.: Arkhimédészi spirál (angol nyelven). Wolfram MathWorld
• Java modell az archimedesi spirális és hasonló görbék interaktív vizsgálatára

Irodalom

• Pattantyús Gépész- és villamosmérnökök kézikönyve 1. kötet. Műszaki Könyvkiadó, Budapest, 1961.