Hiperbolikus spirál

Hiperbolikus spirál (a=2 paraméterrel)

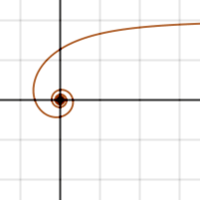
A hiperbolikus spirál egy síkgörbe. Polárkoordinátás egyenlete:

$r={\frac {a}{\theta }}$,

ami az arkhimédészi spirál inverz függvénye. A pólustól végtelen távolságban kezdődik (θ nulla értékéhez r = a/θ végtelen tartozik), egyre „gyorsabban” és „gyorsabban” örvénylik, ahogy közeledik a pólus felé. A görbe bármely pontja és a pólus közötti távolság – a görbe mentén haladva – végtelen.

Az

$x=r\cos \theta ,\qquad y=r\sin \theta ,$

transzformációs összefüggéseket alkalmazva megkapjuk az egyenletét a derékszögű koordináta-rendszerben:

$x=a{\cos t \over t},\qquad y=a{\sin t \over t},$

ahol a t paraméter azonos a θ polárkoordinátával.

A spirálnak y = a (vagis az x tengellyel párhuzamos) aszimptotája van, ha t tart a nullához, akkor y tart a-hoz, és x tart a végtelenhez:

$\lim _{t\to 0}x=a\lim _{t\to 0}{\cos t \over t}=\infty ,$

$\lim _{t\to 0}y=a\lim _{t\to 0}{\sin t \over t}=a\cdot 1=a.$

Egy tetszőleges P pont görbületi sugara:

$\rho =r{({\frac {r^{2}}{a^{2}}}+1)}^{3/2}={\frac {a}{\theta }}{({\frac {\sqrt {1+\theta ^{2}}}{\theta }})}^{3}$

Az r sugár és az érintő szöge a

$\cos \alpha =-{\frac {1}{\sqrt {1+\theta ^{2}}}};$

vagy a

$\sin \alpha ={\frac {\theta }{\sqrt {1+\theta ^{2}}}};$

összefüggésből számítható.

Források

• Pattantyús Gépész- és Villamosmérnökök Kézikönyve 2. kötet. Műszaki Könyvkiadó, Budapest, 1961.