Penrose-féle csempézés

A Penrose-féle csempézés az aperiodikus csempehalmazok (illetve az azokkal való csempézések) egy olyan csoportja, amit Roger Penrose (és tőle függetlenül Robert Ammann) fedezett fel.

Penrose először 1973-ban talált egy 6 csempéből álló aperiodikus csempehalmazt. Az első csempehalmazt, ami bizonyítottan aperiodikus volt, Berger 1966-ban találta, és 20 426 csempéből állt. Ezek a csempék négyszögek voltak, melyeknek az oldalait úgy változtatták meg, hogy a periodicitást elkerüljék. Később sikerült lecsökkentenie a csempék számát 104-re, majd 92-re. Raphael M. Robinson 1971-ben egy 6 csempéből álló halmazt talált. Ez is hat módosított négyzetet tartalmazott. Penrose hat csempéje szabályos hatszögekből állt, és csillagszerű alakzatokból, ezzel megtörte a négyzetek egyeduralmát és azt a sejtést is megdöntötte, miszerint csak módosított négyzetekkel lehet nemperiodikusan lefedni a síkot.

A Penrose-csempézés tulajdonságai[szerkesztés]

A rombuszoknak ez a módosítása és az ábrái nem szükségesek, csak arra szolgálnak, hogy kizárják a helytelen összeillesztést

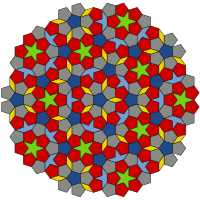
Penrose ezután még sokat foglalkozott a csempékkel, és még két, egyenként két-két csempéből álló aperiodikus halmazt talált.

Az egyik ilyen csempehalmaz két rombuszt tartalmaz:

A kövér rombusznak {72, 72, 108, 108} fokosak a szögeik
A sovány rombusznak {36, 36, 144, 144} fokosak a szögeik.

A csempéket egy egyszerű szabály szerint illesztjük egymáshoz: a két rombusz nem alkothat soha paralelogrammát. Könnyítésként megjelölhetjük az oldalakat, hogy tudjuk, hogy melyik oldalhoz melyiket illeszthetjük. Használhatunk erre a célra színeket, vagy megfelelő módon megváltoztathatjuk a rombuszok oldalait, hogy azokat csak úgy lehessen összeérinteni, hogy a kapott csempézés ne legyen periodikus.

A másik ismert, két csempéből álló halmaz két deltoidot tartalmaz:

Egy konvexet, amit sárkánynak és
egy konkávat, amit dárdának hívunk.

A deltoidok rövidebb oldala 1, a hosszabb pedig ${\tau }={\frac {1+{\sqrt {5}}}{2}}$ , amit szokás aranyszámnak is hívni, hiszen az aranymetszésnél a megfelelő két hossz aránya is ez a szám. Az aranyszám sok helyen előbukkan a csempézés tulajdonságai között:

A sárkányok ${\tau }$ -szor annyian vannak, mint a dárdák.
A területek aránya is ${\tau }$ -szoros.
A csempézés nem-periodikusságának egyik bizonyításában is döntő szerepe van, hiszen a ${\tau }$ egy irracionális szám.

A Penrose-csempék ugyan nem ismétlődő, nem periodikus alakzatokat hoznak létre, a mintának mégis vannak bizonyos periodikusság látszatát nyújtó jellegzetességei, egyfajta rendezettsége. A rombuszokból álló csempézetben például szabályos tízszögek jelennek meg, amik mindenütt azonos állásúak – minden egyes tízszög élei párhuzamosak az összes többiével. Ezek egymásba olvadó elemi celláknak tűnnek. Kváziszimmetriát mutat 72°-os elforgatásra (ötfogású szimmetria). Ez azért is érdekes, mert periodikusan ismétlődő elemi cellákból álló sík- vagy térbeli alakzat nem mutathat ötös szimmetriát. (Ötszögekkel ugyanis nem lehet maradéktalanul lefedni a síkot.)

Néhány példa[szerkesztés]

Név	Alap	1. iteráció	2. iteráció	3. iteráció
Félsárkány
Félnyíl
Nap
Csillag

Kvázikristályok[szerkesztés]

Bár először csak mint érdekes matematikai játék és struktúra jelent meg a Penrose-féle nemperiodikus csempézés, 1984-ben felfedeztek egy ötvözetet, az Al₆Mn-t, aminek a szerkezete a Penrose-féle csempézés térbeli változata. Így a csempézés tulajdonságainak vizsgálata elősegítette az ötvözet tulajdonságainak megértését. Egyébként ez az ötvözet külsőleg mint kristály viselkedett, de rövid időre megkérdőjelezte a szilárdtestfizika alapfeltevését, miszerint egy kristály szerkezete csak 2-es, 3-as, 4-es vagy 6-os forgásszimmetriát mutathat. Már tudjuk, hogy ezek nem igazi kristályok, ezért kvázikristálynak nevezik.

Tízszögű csempe[szerkesztés]

A Penrose-csempézésben megjelenő tízszögletű alakzat miatt felmerült a lehetősége, hogy egyetlen tízszögű csempével is megoldható lenne a feladat. 1996-ban Petra Gummelt igazolta, hogy egy tízszögű csempe két lehetséges megengedett átfedésével nemperiodikus síklefedés hozható létre.

Források[szerkesztés]

Penrose, Roger. (1989) The Emperor's New Mind. (ISBN 0-19-851973-7)
- magyarul: Roger Penrose: A császár új elméje, Akadémiai Kiadó, 1993
Csonka Dorottya (2004. november (XII. évf./5. szám) A nem periodikus Penrose-csempézés. Matematika Tanítása (MS-9101)

David R. Nelson (1986). „Kvázikristályok”. Scientific American (magyar kiadás) (10), 25-33. o.

Külső hivatkozások[szerkesztés]