Meander (matematika)
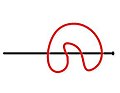
A matematikában a meander vagy zárt meander egy olyan hurokmentes (magát nem metsző) görbe, mely többször metsz egy egyenest. Nevét a folyókanyarulatot jelentő meanderről kapta. Úgy képzelhetünk el egy meandert, mint az útvonalunkat, amint egy folyó fölötti összes hídon átmegyünk egyszer, és visszaérünk oda, ahonnan indultunk.
Meander
[szerkesztés]Adott egy irányított E egyenes az euklideszi síkon (R2). Egy n-edrendű meander egy önmagát nem metsző (hurokmentes) zárt görbe, amely 2n helyen metszi E-t. Két meander akkor ekvivalens, ha topológiailag izomorf (homeomorf).
Példák
[szerkesztés]Az elsőrendű (n=1) meander az E egyenest két pontban metszi.
A másodrendű (n=2) meander az E egyenest négy pontban metszi.
Meandrikus számok
[szerkesztés]A különböző n-edrendű meanderek számát az n-edik meandrikus számnak hívjuk. Az első tizenöt meandrikus szám lejjebb látható (A005315 sorozat az OEIS-ben)
- M1 = 1
- M2 = 2
- M3 = 8
- M4 = 42
- M5 = 262
- M6 = 1828
- M7 = 13 820
- M8 = 110 954
- M9 = 933 458
- M10 = 8 152 860
- M11 = 73 424 650
- M12 = 678 390 116
- M13 = 6 405 031 050
- M14 = 61 606 881 612
- M15 = 602 188 541 928
Meanderpermutáció
[szerkesztés]
(1 8 5 4 3 6 7 2)
Egy meandervonal metszéseit a vonalon megszámozva, majd a görbe érintési sorrendjébe rakva többféle számsort is kaphatunk, ugyanis a görbét többféleképpen lehet megrajzolni. Ez egy permutáció. A közmegegyezés szerint az 1-es számmal a bal szélen indul a számozás, és itt a görbe felfelé halad. Megfigyelhető, hogy felváltva páros és páratlan számokat érint.
Nyílt meander
[szerkesztés]Adott egy irányított E egyenes az euklideszi síkon (R2). Egy n-edrendű nyílt meander egy olyan önmagát nem metsző irányított görbe R2-ben, mely n-szer metszi E-t.
Példák
[szerkesztés]Az elsőrendű meander egy pontban metszi az egyenest.
A másodrendű meander két pontban metszi az egyenest.
Nyílt meandrikus számok
[szerkesztés]A különböző n-edrendű nyílt meanderek számát nevezzük az n-edik meandrikus számnak. Jele:mn Különböző alatt az egymással nem homeomorf meandereket értjük. Íme az első 15 nyílt meandrikus szám: (A005316 sorozat az OEIS-ben)
- m1 = 1
- m2 = 1
- m3 = 2
- m4 = 3
- m5 = 8
- m6 = 14
- m7 = 42
- m8 = 81
- m9 = 262
- m10 = 538
- m11 = 1828
- m12 = 3926
- m13 = 13820
- m14 = 30694
- m15 = 110954
Félmeanderek
[szerkesztés]Adott egy F félegyenes az euklideszi síkon (R2). Egy n-edrendű félmeander egy olyan önmagát nem metsző zárt görbe, mely n-szer metszi F-et. Két félmeander ekvivalens, ha homeomorfak a síkban.
Példák
[szerkesztés]Az elsőrendű félmeander egyszer metszi F-et.
A másodrendű félmeander kétszer metszi F-et.
Félmeandrikus számok
[szerkesztés]A különböző n-edrendű félmeanderek számát nevezzük az n-edik félmeandrikus számnak. Jele: Mn (Gyakran felülvonással jelölik alulvonás helyett) Az első 15 félmeandrikus szám a következő (A000682 sorozat az OEIS-ben).
- M1 = 1
- M2 = 1
- M3 = 2
- M4 = 4
- M5 = 10
- M6 = 24
- M7 = 66
- M8 = 174
- M9 = 504
- M10 = 1406
- M11 = 4210
- M12 = 12198
- M13 = 37378
- M14 = 111278
- M15 = 346846
Összefüggések a meandrikus számok között
[szerkesztés]Meandrikusról nyílt meandrikus számokra fenn áll a következő injektív leképezés:
- Mn = m2n‒1
Minden meandrikus szám rendre két félmeandrikus közé esik:
- Mn ≤ Mn ≤ M2n
A másodiktól kezdve (n>1) minden meandrikus szám páros:
- Mn ≡ 0 (mod 2)
Fordítás
[szerkesztés]- Ez a szócikk részben vagy egészben a Meander (mathematics) című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.