Másodrendű nyomatékok listája
A következő táblázat egyes síkidomok másodrendű nyomatékainak a listája. A másodrendű nyomaték dimenziója hosszúság4, nem szabad összetéveszteni a tehetetlenségi nyomatékkal.
| Leírás | Ábra | Másodrendű nyomaték | Megjegyzés | Forrás |
|---|---|---|---|---|
| teli kör sugárral |  |
[1] | ||
| körgyűrű belső és külső sugárral | 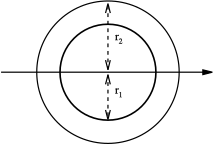 |
|||
| körcikk középponti szöggel radiánban és sugárral a középponton átmenő vízszintes tengelyre |  |
|||
| félkör sugárral súlyponti vízszintes tengelyre |  |
A súlypont távolsága az alaptól | [2] | |
| félkör az alapegyenesére |  |
[2] | ||
| félkör a függőleges szimmetriatengelyre |  |
[2] | ||
| a negyedkör sugárral |  |
[3] | ||
| negyedkör mint fent, de a függőleges vagy vízszintes súlyponti tengelyre |  |
A súlypont a vízszintes és függőleges egyenes oldaltól távolságra van | [3] | |
| ellipszis és féltengelyekkel |  | |||
| téglalap alappal és magassággal |  |
[4] | ||
| téglalap mint fenn, de az alapra |  |
[4] | ||
| háromszög alappal és magassággal súlyponti tengelyre |  |
A súlypont az alaptól távolságra van | [5] | |
| háromszög az alapjára |  |
[5] | ||
| hatszög oldalhosszúsággal |  |
Az eredmény mind a vízszintes, mind a függőleges súlyponti tengelyre igaz |
Kapcsolódó szócikkek[szerkesztés]
Források[szerkesztés]
- ↑ Circle. eFunda. (Hozzáférés: 2006. december 30.)
- ↑ a b c Circular Half. eFunda. (Hozzáférés: 2006. december 30.)
- ↑ a b Quarter Circle. eFunda. (Hozzáférés: 2006. december 30.)
- ↑ a b Rectangular area. eFunda. (Hozzáférés: 2006. december 30.)
- ↑ a b Triangular area. eFunda. (Hozzáférés: 2006. december 30.)
























