Gyorsrendezés
| Gyorsrendezés | |
 | |
| Kategória | rendezési algoritmus |
| Adatstruktúra | tömb |
| Legrosszabb időbonyolultság | |
| Legjobb időbonyolultság | |
| Átlagos idő bonyolultság | |
| Legrosszabb tár bonyolultság | |

A gyorsrendezés vagy quicksort algoritmus egy tömb elemeinek sorba rendezésére. Charles Antony Richard Hoare találmánya, egyike azon rendezéseknek, amiknek a bonyolultsága átlagos esetben . A gyorsrendezés általában gyorsabb az egyéb rendezéseknél, mert a belső ciklusa a legtöbb architektúrán nagyon hatékonyan implementálható, és az adatok jellegének ismeretében az algoritmus egyes elemei megválaszthatóak úgy, hogy csak nagyon ritkán fusson négyzetes ideig.
A gyorsrendezés egy összehasonlító rendezés, és – hatékonyan implementálva – nem stabil rendezés.
Története[szerkesztés]
A gyorsrendezést 1960-ban, az Elliott Brothers angol számítógépgyártónak dolgozva fejlesztette ki Hoare.[1]
Működése[szerkesztés]
A gyorsrendezés oszd meg és uralkodj elven működik: a rendezendő számok listáját két részre bontja, majd ezeket a részeket rekurzívan, gyorsrendezéssel rendezi. A felbontáshoz kiválaszt egy támpontnak nevezett elemet (más néven pivot, főelem vagy vezérelem), és particionálja a listát: a támpontnál kisebb elemeket eléje, a nagyobbakat mögéje mozgatja. Teljes indukcióval könnyen belátható, hogy ez az algoritmus helyesen működik.
Az algoritmus pszeudokódja:
function quicksort(array)
var list less, equal, greater
if length(array) ≤ 1
return array
select a pivot value pivot from array
for each x in array
if x < pivot then append x to less
if x = pivot then append x to equal
if x > pivot then append x to greater
return concatenate(quicksort(less), equal, quicksort(greater))
Helyben rendező változat[szerkesztés]
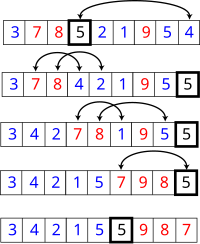
A fenti változat tárhelyet igényel, azaz annyit, amennyit az összefésüléses rendezés. A gyorsrendezés helyben is elvégezhető: az alábbi implementációban a partition eljárás az array tömb left és right közötti elemeit a pivotIndex elem két oldalára gyűjti:
function partition(array, left, right, pivotIndex)
pivotValue := array[pivotIndex]
swap array[pivotIndex] and array[right] // Move pivot to end
storeIndex := left
for i from left to right // left ≤ i < right
if array[i] ≤ pivotValue
swap array[i] and array[storeIndex]
storeIndex := storeIndex + 1
swap array[storeIndex] and array[right] // Move pivot to its final place
return storeIndex
function quicksort(array, left, right)
if right > left
select a pivot index (e.g. pivotIndex := left)
pivotNewIndex := partition(array, left, right, pivotIndex)
quicksort(array, left, pivotNewIndex-1)
quicksort(array, pivotNewIndex+1, right)
A particionálás során a sorrend megváltozik, azaz ez már nem stabil rendezés.
Bonyolultsága[szerkesztés]
Ha minden particionálás felezné a listát, akkor a rekurziót egy mélységű fával lehetne ábrázolni, és mivel a fa minden szintjén összesen elem van (csak egyre több partícióban), az egyes szinteken a particionálásokhoz szükséges összes lépésszám lenne, azaz az algoritmus összesen lépést igényelne. Ez általában is igaz, ha a nagyobb és a kisebb partíció aránya korlátos: ha például a kisebb partícióba mindig legalább az elemek 1%-a kerül, a fa még mindig legfeljebb mély. A legrosszabb esetben azonban, ha az egyik lista mindig egyelemű, a fa lineáris lesz, és mélységű, azaz összesen lépés kell, vagyis a gyorsrendezés nem teljesít jobban, mint a beszúrásos vagy a kiválasztásos rendezés.
Ha a támpontot véletlenszerűen választjuk, akkor a várható bonyoultság mindig lesz: minden lépésben 50% eséllyel választunk olyan támpontot, hogy a rövidebb listába legalább az elemek negyede kerül, és legfeljebb ilyen vágás után eljutunk az egyelemű listáig, azaz a várható mélység . Az átlagos eset lényegében azonos ezzel: az elemek egy véletlen permutációján futtatni az algoritmust ugyanaz, mintha véletlenül választanánk.
Formálisabban, az összehasonlítások átlagos száma a következő rekurzív egyenlettel számítható:
ahol a támpont összehasonlítása a partíció összes tőle különböző elemével, az összeg másik tagja pedig a lehetséges particionálások átlaga. Ez azt jelenti, hogy a gyorsrendezés átlagosan csak körülbelül 39%-kal lassabb, mint legjobb esetben.
A levezetés részletesebben:
Gyors kiválasztás[szerkesztés]
A gyorsrendezés alapötlete kiválasztó algoritmusoknál is alkalmazható: ha egy lista k-adik legkisebb elemét kell kiválasztani, akkor a partíciók hosszából minden lépésben meg tudjuk mondani, melyikben van, tehát elég egyszeres rekurziót használni, amiből átlagos futásidő adódik. Az algoritmus módosításával a legrosszabb esetbeni idő is elérhető.
A lépésigényű kiválasztó algoritmust a gyorsrendezésben felhasználva választhatjuk minden lépésben a mediánt támpontnak, így a futásidő a legrosszabb esetben is lesz. A gyakorlatban ezt ritkán használják, mert átlagosan valamivel lassabb.
Kapcsolat más rendezőalgoritmusokkal[szerkesztés]
A gyorsrendezés a rendezőfa egy speciális változatának is felfogható: ahelyett, hogy sorban beszúrnánk az elemeket egy fába, a rekurzív hívások adják a fastruktúrát.
A gyorsrendezés két fő vetélytársa a kupacrendezés és az összefésüléses rendezés. Mindkettő átlagos és legrosszabb esetben is lépésigényű. Az összefésüléses rendezés stabil, és nagyon hatékony láncolt listákon és lassú elérésű tárban (például a merevlemezen) tárolt listákon, de tömbökön nagy a helyigénye. A kupacrendezésnek kisebb a helyigénye, mint a gyorsrendezésnek, de átlagban valamivel lassabb.
Irodalom[szerkesztés]
- Brian C. Dean, "A Simple Expected Running Time Analysis for Randomized 'Divide and Conquer' Algorithms." Discrete Applied Mathematics 154(1): 1-5. 2006.
- Hoare, C. A. R. "Partition: Algorithm 63," "Quicksort: Algorithm 64," and "Find: Algorithm 65." Comm. ACM 4(7), 321-322, 1961
- R. Sedgewick. Implementing quicksort programs, Comm. ACM, 21(10):847-857, 1978.
- David Musser. Introspective Sorting and Selection Algorithms, Software Practice and Experience vol 27, number 8, pages 983-993, 1997
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 113–122 of section 5.2.2: Sorting by Exchanging.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 7: Quicksort, pp. 145–164.
- A. LaMarca and R. E. Ladner. "The Influence of Caches on the Performance of Sorting." Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, 1997. pp. 370–379.
- Faron Moller. Analysis of Quicksort. CS 332: Designing Algorithms. Department of Computer Science, University of Wales Swansea.
- Steven Skiena. Lecture 5 - quicksort. CSE 373/548 - Analysis of Algorithms. Department of Computer Science. State University of New York at Stony Brook.
- Conrado Martínez and Salvador Roura, Optimal sampling strategies in quicksort and quickselect. SIAM J. Computing 31(3):683-705, 2001.
- Jon L. Bentley and M. Douglas McIlroy, "Engineering a Sort Function, SOFTWARE---PRACTICE AND EXPERIENCE, VOL. 23(11), 1249—1265, 1993
Források[szerkesztés]
- ↑ Timeline of Computer History: 1960. Computer History Museum
További információk[szerkesztés]
- Gyorsrendezés különböző programnyelveken Archiválva 2008. május 9-i dátummal a Wayback Machine-ben a LiteratePrograms oldalon
- A gyorsrendezés szemléltetése külüllőmenti legényes tánccal















