Ulam-spirál
|
|
Ez a szócikk vagy szakasz lektorálásra, tartalmi javításokra szorul. |
Az Ulam-spirál vagy prím-spirál a számelméletben a prímszámok egy spirális elrendezése, ami egy máig megmagyarázatlan mintát mutat. Nevét felfedezőjéről, Stanisław Ulam lengyel matematikusról kapta, aki 1963-ban egy értekezleten unalmában rajzolta fel a spirált.
Ulam egy négyzetrács mentén, spirálvonalban haladva felrajzolta az első 50 pozitív egész számot:

Ezután kihúzta azokat, amik nem prímek, és a következő ábrát kapta:
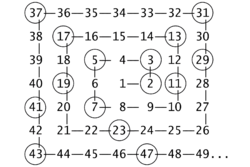

Meglepetésére a prímek többnyire átlók mentén helyezkedtek el. A jelenség nagyobb léptékben is megfigyelhető, például az oldalsó ábrán látható 200 × 200-as spirálban, ahol a prímeket fekete pontok jelzik.
Mivel a páros számok a 2-t kivéve mind összetettek, és a spirálban a sakktábla sötét kockáihoz hasonló mintában helyezkednek el, az önmagában nem meglepő, hogy a prímszámok egy átlós rácsot alkotnak, az viszont igen, hogy ezen rács egyes vonalain sokkal gyakrabban fordulnak elő, mint másokon. Ez akkor is igaz lesz, ha a számokat nem egytől kezdve írjuk fel. Képletben megfogalmazva, sok olyan b és c konstans van, amire az függvény sűrűn ad helyettesítési értékként prímeket. A jelenség oka máig ismeretlen.
Elég messziről nézve az ábrát függőleges és vízszintes vonalak is kirajzolódnak.
A Leonhard Euler által talált kifejezés minden 0 és 15 közötti értékre prímszámot ad. Ezek a prímek: 17, 19, 23, 29, 37, 47, 59, 73, 89, 107, 127, 149, 173, 199, 227 és 257 megjelennek az Ulam-spirál főátlóján. Euler később egy másik képletet is talált , ami 0 és 40 közötti helyettesítési értékekre prímet ad. Ez egy másik átló, ami mentén különösen sok a prím: 10 millióig a helyettesítési értékek 47,5%-a prímet ad. Ulam további képleteket is talált, amik majdnem ilyen jók.
A Hardy–Littlewood-féle F-sejtés[szerkesztés]
Egy 1923-ban megjelent cikkükben Hardy és Littlewood a Goldbach-sejtésen kívül még más sejtésekkel is foglalkoztak. Ezek között vannak olyanok is, amik megmagyaráznák az Ulam-spirált, ha bebizonyosodnának. az F-sejtés a Bateman–Horn-sejtés speciális esete, ami aszimptotikus képletet ad az ax2+bx+c alakú prímekre. A vízszintessel és függőlegessel 45 fokos szöget bezáró sugárirányú egyeneseken levő számok a 4x2+bx+c alakú polinomok helyettesítési értékeinek felelnek meg, ahol b páros. Az F-sejtés szerint a prímek sűrűsége érzékeny a diszkriminánsra, b2-16c-re.
Az F-sejtés így szól:
Legyen az ax2+bx+c egész együtthatós polinomban a pozitív. Ekkor, ha a polinom együtthatóinak legnagyobb közös osztója nagyobb, mint egy, vagy a diszkriminánsa teljes négyzet, akkor a polinom felbontható, így összetett számokat ad, ha x természetes szám.
Sőt, ha az ax2+bx+c polinomban a+b, és c is páros, akkor természetes számokat helyettesítve csak páros helyettesítési értékek adódnak, amik a 2 kivételével összetettek.
Hardy és Littlewood szerint ezektől az esetektől eltekintve a polinom végtelen sok x-re ad prímet helyettesítési értékként, ha x végigfutja a természetes számokat.
Az F-sejtés a Bunyakovszkij-sejtés speciális esete, és mint ilyen, máig megoldatlan. Jelölje P(n) ax2+bx+c polinom által helyettesítési értékként kapható n-nél kisebb prímek számát! Ekkor Hardy és Littlewood szerint
ahol A csak a-tól, b-től, és c-től függhet, de n-től nem. A prímszámelmélet szerint, ha ez a képlet 1 körüli értékeket ad, akkor a prímek eloszlása a másodfokú polinom helyettesítési értékeiként véletlenszerűnek tekinthető. De, ha ez a szám 1-nél nagyobb, vagy kisebb, akkor a ax2+bx+c polinomok sok, vagy kevés prímet ad. A 4x2-2x+41 polinom nagyon gazdag prímekben, ami az Ulam-spirálon is látható. Ez a polinom megkapható az Euler által talált x2-x+41 prímgeneráló polinomból az x=-2x+1 helyettesítéssel. A képlet erre a polinomra 6,6-et ad, vagyis ennyiszer több prímet ad, mint amennyi véletlenszerűen lenne.
Hardy és Littlewood képlete A-ra:
Az első tényezőben p a és b közös prímtényezője; a második szorzatban egy a-hoz relatív prím prím. ε=0, ha a+b páros, és ε=1, ha az összeg páratlan. Legendre-szimbólum.
Jacobson és Williams talált egy másodfokú polinomot, amire A ≈ 11,3. Eddig ez a legnagyobb ismert érték. Jacobson and Williams.[1][2]
Lásd még[szerkesztés]
Források[szerkesztés]
- ↑ Jacobson Jr., M. J. & Williams, H. C (2003), "New quadratic polynomials with high densities of prime values", Mathematics of Computation 72: 499–519, DOI 10.1090/S0025-5718-02-01418-7
- ↑ Guy, Richard K. (2004), Unsolved problems in number theory (3rd ed.), Springer, p. 8, ISBN 978-0387208602, <https://books.google.com/?id=1AP2CEGxTkgC&printsec=frontcover>
- Stein, M. and Ulam, S. M. (1967), "An Observation on the Distribution of Primes." American Mathematical Monthly 74, 43-44.
- Stein, M. L.; Ulam, S. M.; and Wells, M. B. (1964), "A Visual Display of Some Properties of the Distribution of Primes." American Mathematical Monthly 71, 516-520.
- Gardner, M. (March 1964), "Mathematical Recreations: The Remarkable Lore of the Prime Number", Scientific American 210: 120–128.
- Hardy, G. H. & Littlewood, J. E. (1923), "Some Problems of `Partitio Numerorum'; III: On the Expression of a Number as a Sum of Primes", Acta Mathematica 44: 1–70, DOI 10.1007/BF02403921.
- Stein, M. L.; Ulam, S. M. & Wells, M. B. (1964), "A Visual Display of Some Properties of the Distribution of Primes", American Mathematical Monthly (Mathematical Association of America) 71 (5): 516–520, doi:10.2307/2312588, <http://www.jstor.org/stable/2312588>.
- Stein, M. & Ulam, S. M. (1967), "An Observation on the Distribution of Primes", American Mathematical Monthly (Mathematical Association of America) 74 (1): 43–44, doi:10.2307/2314055, <http://www.jstor.org/stable/2314055>.
- Prime Spiral, MathWorld
- Paul Hoffman: A prímember
Külső hivatkozások[szerkesztés]
- Le Village Premier – az Ulam-spirál első százezer elemét vizsgáló Java applet
- Prime numbers in PostScript Archiválva 2007. szeptember 10-i dátummal a Wayback Machine-ben – PostScript program az Ulam-spirál elemeinek megjelenítésére
- Java applet forráskóddal
- http://www.abarim-publications.com/artctulam.html
- http://www.numberspiral.com/







