Szúdoku



A szúdoku (数独; Hepburn: sudoku) egy logikai játék, melyben megadott szabályok szerint számjegyeket kell elhelyezni egy táblázatban. Legközönségesebb változatában egy 9×9-es táblázat van 3×3 = 9 darab 3×3-as résztáblázatra felosztva, és minden résztáblázatot az 1, 2, 3, 4, 5, 6, 7, 8, 9 számokkal kell kitölteni úgy, hogy az egész 9×9-es táblázat minden sorában és minden oszlopában az 1...9 számok mindegyike egyszer forduljon elő. A rejtvény készítője a megoldhatóság érdekében előre ki szokta tölteni néhány szükséges számmal a 9×9-es táblázat bizonyos celláit – általában úgy, hogy csak egy megoldása (kitöltése) létezzen a rejtvénynek. A rejtvényfejtő feladata kitölteni a maradék cellákat a fentebb írt feltételeknek megfelelően.
A szúdoku[szerkesztés]
A „szúdoku” név egy hosszabb japán kifejezés rövidítése. Az eredeti név jelentése: „a számjegyek csak egyszer szerepelhetnek” (数字は独身に限る, szúdzsi va dokusin ni kagiru). Ez a japán Nikoli Co. Ltd. bejegyzett védjegye.
A megoldott szúdoku egy speciális latin négyzet. Latin négyzetekkel kapcsolatos munkássága miatt sokan úgy tartják, a játék ötlete Leonhard Eulertől származik. A szimmetrikus (egymásba tükrözhető, forgatható) megoldások megkülönböztetésétől eltekintve, a 9×9-es szúdoku lehetséges kitöltéseinek száma 6 670 903 752 021 073 000 000, azaz közel 6,7 trilliárd.[1]
A játék ma ismert változatát az amerikai Howard Garns alkotta meg 1979-ben. A rejtvényt a Dell Magazines adta ki Number Place címmel. A játék 1986-ban nagy népszerűségre tett szert Japánban, mikor a Nikoli kiadta a játék japán változatát. A nemzetközi siker 2005-ben érkezett el.
Változatai[szerkesztés]
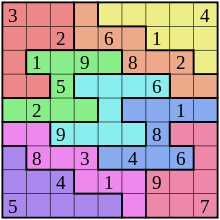



A hagyományos szúdokukban minden mező több olyan blokk része, mely blokkban minden szám (betű) pontosan egyszer szerepelhet. A nem hagyományos szúdokukban a mezőre más szabály is vonatkozik.
Hagyományos szúdokuk[szerkesztés]
Négyzet alakú változatok (zárójelben az egyes blokkok mérete):
- Kisebb táblás verziók: 4×4 (2×2), 6×6 (2×3) és 8×8 (2×4).
- Nagyobb táblás verziók: 12×12 (3×4), 16×16 (4×4), 20×20 (4×5) és 25×25 (5×5).
- Szúdoku X: az átlókat is a szabályoknak megfelelően kell kitölteni.
- 3D szúdoku: a szúdoku háromdimenziós változata több formában létezik, például a Sudokube, amit Rubik Ernőnek köszönhetünk.
Az X-szúdoku annyiban különbözik a többitől, hogy az átlóbeli elemek nem három (sor, oszlop, blokk), hanem négy blokkhoz tartoznak.
Nem négyzetes változatok:
- Szamuráj szúdoku: több négyzetes szúdoku egyesítése.
- Renban (amőba) szúdoku: ugyanazok a szabályai mint az eredetinek, de nem szabályos 3 × 3-as területek vannak, hanem szabálytalan, egybefüggő területek. Ez az ember számára (aki vizuális információkat használ a megfejtéskor) nagy különbségnek tűnik; a számítógép „észre sem veszi” a különbséget. A lényeg ui. nem az, hogyan helyezkednek el a blokk mezői, hanem az, hogy mely mező mely blokkban szerepel.
Az „összenőtt” szúdokuk számos más verziója ismert a szamuráj szúdokun kívül.
Nem hagyományos szúdokuk[szerkesztés]
Az ilyen szúdokukban minden mező a szokásos három hagyományos blokk tagja (sor-, oszlop ill. blokk), és ezen felül valamilyen más típusú reláció is érvényes rá:
- Szúdoku gusu: a szürkével megjelölt mezőkbe csak páros számok (2, 4, 6, 8) kerülhetnek, egyébként a szabályok az eredetiek.
- Killer (gyilkos) szúdoku: az eredeti szabályokon felül a megjelölt területeken levő számok összege is adott.
- Kisebb-nagyobb szúdoku: az egy blokkhoz tartozó szomszédos mezőknél adott, melyik elem a kisebb ill. nagyobb.
Világbajnokságok[szerkesztés]
- Az első szúdoku-világbajnokságot 2006. március 10. és 12. között rendezték meg az olaszországi Luccában. A versenyt egy 31 éves cseh könyvelő, Jana Tylová nyerte. A magyar Gyimesi Zoltán sakknagymester a 12. helyet szerezte meg[2]
- A második szúdoku-világbajnokságra 2007. március 28. és április 1. között került sor a cseh fővárosban, Prágában. Az egyéni versenyt az amerikai Thomas Snyder nyerte, a csapatversenyben pedig Japán diadalmaskodott. Hazánk csapatversenyben a negyedik helyet szerezte meg.
- A harmadik szúdoku-világbajnokságot 2008. április 14. és 17. között az indiai Goában rendezték meg. Az egyéni versenyt ezúttal is az előző évi bajnok amerikai Thomas Snyder nyerte, a csapatversenyben pedig a cseh csapat vitte el a pálmát.
- A negyedik szúdoku-világbajnokság 2009. április 24. és 27. között a felvidéki Zsolnán zajlott. Az egyéni versenyt a lengyel Jan Mrozowski, a csapatversenyt pedig a házigazda Szlovákia nyerte.
- Az ötödik szúdoku-világbajnokságon, amely 2010. április 29. és május 2. között Philadelphiában zajlott, egyéniben ezúttal a lengyel Jan Mrozowskinak sikerült dupláznia, csapatban pedig Németország lett az első. A magyar csapat a harminc induló nemzet között a tizedik helyen végzett.
- A hatodik világbajnokságot 2011. november 6. és november 11. között hazánkban, Eger városában rendezték, az amerikai Thomas Snyder nyerte egyéniben, csapatban a németek maguk mögé utasították az ezüstérmes cseh és a bronzérmes amerikai együttest. A magyar csapat a 19. lett.
- A hetedik szúdoku-világbajnokságnak 2012. október 1. és október 3. között a horvátországi Krajlevica adott otthont. Egyéniben Jan Mrozowski, csapatban pedig Japán nyert, a magyar csapat a nyolcadik lett ezúttal.
Számítógépes megoldások[szerkesztés]
Többen foglalkoztak már szúdoku problémák számítógépes megfejtésével, de mindezideig nem volt sikeres általános számítógépes megoldás. A helyzet azonban radikálisan megváltozott az utóbbi időkben. Két, az Egyesült Államokban, a Notre Dame egyetemen (teljes név University of Notre dame du Lac), az elméleti fizika egyik ágában, bonyolult számítástechnikai optimálás algoritmus problémáin (angolul: boolean SATisfiability problem) dolgozó magyar elméleti fizikus, Toroczkai Zoltán és Ercsey-Ravasz Mária kidolgozott egy általános megoldást, ami nagyon gyorsan old meg minden szúdokuproblémát.[3]
A kutatók azonban úgy látják, hogy algoritmusos megoldásuknak lehet ipari és tudományos (például számítástechnikai illetve biológiai) alkalmazása is számos és változatos problémák megoldására.
Jegyzetek[szerkesztés]
- ↑ D. R. Mazur: Combinatorics - A Guided Tour . Google könyvek. Beill.: 2016-7-12.
- ↑ Hübners who-is-who. (Hozzáférés: 2014. április 21.)
- ↑ [1] Ferard, Émeline: Des chercheurs trouvent une formule pour résoudre tous les sudokus. Gentside Découverte, 2012. Legutóbbi hozzáférés: 2014. május 16.
Kapcsolódó szócikkek[szerkesztés]
További információk[szerkesztés]
- A szúdokuk lelkivilága. Mi a minimum szúdoku?
- Varga Valéria: Sudoku (Szakdolgozat)
- Szúdokuvariációk Archiválva 2007. február 19-i dátummal a Wayback Machine-ben
- Szúdokumegoldó Archiválva 2012. szeptember 15-i dátummal a Wayback Machine-ben

