Lorentz-tényező
A Lorentz-tényező számos speciális relativitáselmélettel kapcsolatos fogalomban szerepel, mint az idődilatáció, hosszkontrakció és a relativisztikus tömeg. A Lorentz-tényező a fénysebesség és az aktuális sebesség közötti összefüggésről szól.
Jelölése γ.
A Lorentz-tényező Hendrik Lorentz holland fizikus után kapta a nevét.[1]
ahol:
- a fénysebességhez viszonyított sebesség,
- v az a sebesség, melyet abban a vonatkoztatási rendszerben figyelnek meg, ahol az idő: t
- τ a ‘helyes’ idő
- c a fénysebesség
Megközelítések[szerkesztés]
A Lorentz-tényező kifejtése Taylor-sorban:
A γ ≈ 1 + 1/2 β2 közelítés kis sebességeken jelentkező relativisztikus hatás. Ez a közelítés 1% hibát jelent v < 0,4 c sebességnél (120 000 km/s), és 0,1%-on belüli a hiba 66 000 km/s sebesség alatt.
A két egyenlet:
Kis sebességeken a Taylor-sor csonkított változata lehetővé teszi, hogy a speciális relativitást newtoni mechanikára redukálja:
γ ≈ 1 és γ ≈ 1 + 1/2 β2, ekkor a newtoni egyenletekre redukálódik:
A Lorentz-tényező inverz kifejezésben:
Ennek sorba fejtett formája:
Az első két kifejezés segítségével gyorsan kiszámíthatók a sebességek nagy γ értékektől. A β ≈ 1 - 1/2 γ−2 közelítés 1% hiba alatt van γ > 2 esetén, és 0,1% -n belül, ha γ > 3,5.
Értékek[szerkesztés]
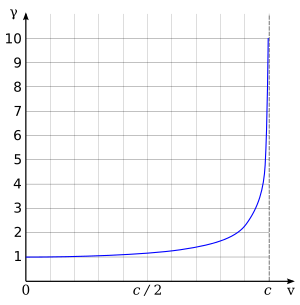
Az alábbi táblázat a Lorentz-tényező értékét és annak reciprokát mutatja néhány esetben. A félkövérrel írt értékek pontosak.
| Sebesség (c-ben mérve) | Lorentz-tényező | Reciproka |
|---|---|---|
| 0.000 | 1.000 | 1.000 |
| 0.050 | 1.001 | 0.999 |
| 0.100 | 1.005 | 0.995 |
| 0.150 | 1.011 | 0.989 |
| 0.200 | 1.021 | 0.980 |
| 0.250 | 1.033 | 0.968 |
| 0.300 | 1.048 | 0.954 |
| 0.400 | 1.091 | 0.917 |
| 0.500 | 1.155 | 0.866 |
| 0.600 | 1.250 | 0.800 |
| 0.700 | 1.400 | 0.714 |
| 0.750 | 1.512 | 0.661 |
| 0.800 | 1.667 | 0.600 |
| 0.866 | 2.000 | 0.500 |
| 0.900 | 2.294 | 0.436 |
| 0.990 | 7.089 | 0.141 |
| 0.999 | 22.366 | 0.045 |
| 0.99995 | 100.00 | 0.010 |
Gyorsaság[szerkesztés]
Ha th r = β, akkor γ = ch r. Itt az r, a hiperbolikus szög, gyorsaságként ismert a relativitáselméletben.[2] A Lorentz-transzformációt alkalmazva látható, hogy a gyorsaság additív, a sebesség viszont nem. Így a gyorsaság paraméter egy úgynevezett - fizikai modelleknél használatos - egyparaméteres csoportot alkot. Szuperlumináris mozgások tárgyalásánál γ–t néha Γ-val jelölik. A Lorentz-tényező szerepel az idődilatáció, a hosszkontrakció és a relativisztikus tömeg tárgyalásakor a speciális relativitáselméletben. A hossza rövidebbnek mérhető, mely a helyi hossz osztva γ-val. A részecskefizikában a gyorsaságot a következőképpen definiálják:[3])
Levezetés[szerkesztés]
Einstein speciális relativitáselméletének egyik alapvető posztulátuma az, hogy minden inercia rendszerben a megfigyelő ugyanazt a sebességet méri a fény esetében, függetlenül az ő relatív mozgásától.
Legyen két megfigyelő (A és B): Az első, A, állandó v sebességgel utazik a másik megfigyelő(B) vonatkoztatási rendszeréhez viszonyítva, ahol B megfigyelő nyugalomban van. A egy lézersugarat irányít “felfelé” ((merőlegesen az utazás vonalára). B perspektívájából a fény szögben érkezik be. Egy , idő után, A távot utazott be; a fény (szintén B szemszögéből) távot tett meg egy bizonyos szögben. A fény komponense a Pitagorasz-tétel alapján:
A távolság, melyet A lát, a fény útja:
majd egyszerűsítve:
Kapcsolódó szócikkek[szerkesztés]
- Relativitáselmélet
- Általános relativitáselmélet
- Speciális relativitáselmélet
- Hendrik Lorentz
- Hosszkontrakció
- Idődilatáció
- Relativisztikus tömeg
- Részecskefizika
- Lorentz-transzformáció
Források[szerkesztés]
- ↑ One universe, by Neil deGrasse Tyson, Charles Tsun-Chu Liu, and Robert Irion.
- ↑ Kinematics Archiválva 2014. november 21-i dátummal a Wayback Machine-ben, by J.D. Jackson, See page 7 for definition of rapidity.
- ↑ Introduction to High-Energy Heavy-Ion Collisions, by Cheuk-Yin Wong, See page 17 for definition of rapidity.






















