Caesar-rejtjel
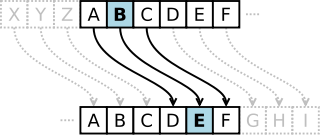
A Caesar-kód vagy Caesar-rejtjel az egyik legegyszerűbb és legelterjedtebb titkosírási módszer. Ez egy helyettesítő rejtjel, ami azt jelenti, hogy minden egyes betűt az ábécében egy tőle meghatározott távolságra lévő betűvel kell helyettesíteni. Így például, ha mondjuk az eltolódás 3, az angol ábécében az A-t a D-vel, a B-t az E-vel stb. kell helyettesíteni. A magyar ábécére vonatkoztatva ez az A betű helyett C-t, az Á betű helyett CS-t jelent. Az elnevezését Julius Caesar után kapta, aki ennek a segítségével kommunikált tábornokaival.
A Caesar által használt titkosírási eljárást több bonyolultabb kriptográfiai módszerbe is beépítették, így a Vigenère-rejtjelbe; ezen kívül ma is használják pl. a ROT13 rendszerben. Azonban, mint bármely más ábécé-helyettesítési módszerről, a Caesar-rejtjelről is elmondható, hogy nagyon könnyű feltörni, így a kommunikációhoz nem nyújt igazi biztonságot.
Általánosabban Caesar-rejtjelnek nevezünk minden olyan rejtjelezést, amelyet az ábécé betűinek átrendezésével kapunk. Ebből a legegyszerűbb a kulcsszavas Caesar-kód, ahol az ábécé egyes betűit előre emeljük, a többit pedig ezután egyszerűen felsoroljuk, és eszerint helyettesítünk.
Története[szerkesztés]

A módszer nevét Julius Caesarról kapta, akiről Suetonius jegyezte meg, hogy hárombetűs eltolást alkalmazott a katonai levelezésében, megvédeni kívánván azt az illetéktelen szemektől. Habár Caesar az első ismert használója, korábbról is vannak gyanított használói. Az unokaöccse, Augustus ugyanezt a rejtjelezést használta, azonban ő a hárommal jobbra helyett az eggyel balra rendszert alkalmazta, valamint a kódábécét nem rotálta, hanem a Z helyett AA jelet írt.
Habár arra vonatkozólag nincs ismeretünk, hogy ez a kódolás a maga korában mennyire volt hatékony, valószínűleg megbízhatónak számított. Emellett tanúskodik, hogy Caesar kiemelt fontosságú információk titkosítására alkalmazta. Nem mellékes szempont, hogy a legtöbb ellenfele írástudatlan volt, míg mások az üzenetet ismeretlen nyelven írtnak tételezhették fel.
A rejtjel megfejtésére vonatkozólag először a 9. századból van említés, Al-Kindi ír róla, a gyakoriságanalízissel kapcsolatban. Ennél korábbi információnk nincsen semmilyen behelyettesítéses rejtjelezés megfejtéséről, így valószínűleg Caesar titkosírását sem fejtették meg addig.
Ugyanezt a titkosítást alkalmazták a mezuzák esetében, csak éppen egy betűnyi eltolással, hogy elrejtsék Isten nevét. Ez valószínűleg abból az időből ered, amikor a zsidóság nem használhatott ilyen eszközöket. Az így kapott betűcsoportokat egyes ortodox irányzatok igen jelentősnek tekintenek a gonosz távol tartása tekintetében.
A kódolás a 19. században a hirdetések körében volt népszerű, elsősorban társkereső és szerelmi témákban. David Kahn 1967-ben azt találta, hogy a The Times oldalain is ilyen formában folytattak egyesek társalgásokat.
Az orosz hadsereg 1915-ben az akkor ismert, erősebb rendszerekkel szemben is ugyanezt a titkosítást alkalmazta, mivel kiderült, hogy a vezetők számára komoly gondot jelent a modern módszerek használata, egyáltalán megtanulása. Következményképpen a német és osztrák hírszerzésnek a legkönnyebb dolga az orosz hadikommunikációval volt.
Manapság is lehet találkozni a Caesar-rejtjellel különféle gyermekjátékokban, illetve Usenet csoportokban, hol egyes történetleírásokat (spoiler) zavarnak össze a Caesar-rejtjelből származó ROT13 kóddal. A gyerekjátékok esetén vagy egy koncentrikus gyűrűpár, vagy egy lemezpár segítségével történik a megfejtés.
A rejtjel továbbfejlesztése a Vigenère-rejtjel, ami több Caesar-rejtjel együttese egy kódszóval kiválasztva. Ha a kulcs hossza legalább az üzenet hosszával egyezik meg, és mindössze egyszeri használatú, akkor a kód bizonyítottan megfejthetetlen. Rövidebb kulcsok esetén a frekvencia-analízis módszereivel a kód feltörhető, bár rendkívül nehéz.
Caesar kódolás megvalósítása[szerkesztés]
Elmélet[szerkesztés]
Kódolás és dekódolás[szerkesztés]
A titkosítás két ábécével megvalósítható úgy, hogy az egyiket a másik alá írva 'n' betűhellyel eltoljuk:
Eredeti: AÁBCDEÉFGHIÍJKLMNOÓÖŐPQRSTUÚÜŰVWXYZ Eltolt: DEÉFGHIÍJKLMNOÓÖŐPQRSTUÚÜŰVWXYZAÁBC
Ekkor egyszerű a titkosítás és a visszafejtés is. Rejtjelezésnél a felső ábécében kikeressük az aktuális betűt, és helyére az alatta lévőt írjuk, fejtésnél pedig ugyanezt visszafelé hajtjuk végre. A fenti példát alkalmazva egy mintaszövegre:
Titkosítandó: ÉN ELMENTEM A VÁSÁRBA FÉL PÉNZZEL Titkos szöveg: IŐ HÓÖHŐŰHÖ D ZEÜEÚÉD ÍIÓ TIŐCCHÓ
A kongruenciák segítségével matematikai formát is adhatunk az eljárásnak, ehhez a betűket számértékként kell tekintsük, mégpedig az A=0, Á=1, B=2, stb. logikával.[1] Ekkor a kódolt ábécét a
formával számolhatjuk ki, ahol 'c' a kódolt betű értéke, 'a' a kódolandó betű értéke, 's' az eltolás, 'n' pedig az ábécé hossza. A visszafejtés hasonlóan történik, a kongruenciák tulajdonságait kihasználva:
Ezen az elven működnek a különböző számítógépes megvalósítások, bár ezek legtöbbször a betűk, mint karakterek számítógépes kódját veszik alapul.
A kulcsszavas Caesar-kód esetén az analízisben használt átrendezésekhez kell nyúlnunk. Ezek valójában bijekciók, így az ábécében lévő szimbólumokat valamely sorozat első elemeinek tekintve a rejtjelezés egyszerűen az átrendezés által adott kép lesz:
ahol cn a kódolt szöveg, mint sorozat egy eleme, an pedig a kódolandó szövegé.
Példának okáért a használt kód legyen a következő:
Titkosítandó ábécé: AÁBCDEÉFGHIÍJKLMNOÓÖŐPQRSTUÚÜŰVWXYZ Kódábécé: ÖÜÓŰQWERTZUIOPŐÚASDFGHJKLÉÁÍYXCVBNM
A titkosítandó szöveg és a titkosított formája ekkor:
Szöveg: EGY MESSZI VÁNDOR JÖTT KI ŐS ROMOK FELŐL REGÉLT[2] Kódolva: WTN ÚWLLMU CÜAQSK OFÉÉ PU GL KSÚSP RWŐGŐ KWTEŐÉ
Ennek a módszernek az előnye az eltolásos ábécéhez képest, hogy lényegesen több (n!, ahol n az ábécé hossza) variációja van, másrészt pedig puszta rotációval nem lehet feltörni, így némileg erősebb titkosításnak tekinthetjük. Természetesen a modern technikákkal szemben, leszámítva a rövid szövegeket, védtelen. Megvalósítása ugyanakkor szoftveresen bonyolultabb, mert a teljes helyettesítést meg kell adnunk.
A kód feltörése[szerkesztés]
| „ | Ha tudjuk, milyen nyelven íródott a kódolt üzenet, akkor megfejtésének egyik módja az, hogy veszünk egy ugyanolyan nyelven írt nyílt szöveget, amely elég hosszú ahhoz, hogy legalább egy lapot megtöltsön, és megszámláljuk, melyik betű hányszor fordul elő benne. A legtöbbször előtaláltat 'első'-nek nevezzük, a gyakoriságban következőt 'másodiknak', a következőt harmadiknak és így tovább, mígnem a nyílt szöveg összes betűjét számba vesszük.
Ezután vesszük a kódszöveget, s annak szimbólumait is megszámláljuk. Megkeressük a legsűrűbben előfordulót, s azt behelyettesítjük a nyílt szöveg leggyakoribb betűjével, a sorban következőt a 'második'-kal, az az utánit a 'harmadik'-kal, és így tovább, míg be nem helyettesítjük a megfejteni kívánt szöveg minden szimbólumát. |
” |
| – Al-Kindi - Titkos üzenetek megfejtése | ||
Ha ismeretlen kód kerül a kezünkbe, és szeretnénk visszafejteni, két eset lehetséges:
- nem tudjuk, milyen rendszerben van kódolva, de tudjuk, hogy egyszerű behelyettesítéses módszerrel;
- ismeretes, hogy Caesar-rendszerben van rejtjelezve, de nem tudjuk, milyen eltolással.
Ennek megfelelően a visszafejtés is kétféleképpen történhet.
Mindenféleképpen segítséget nyújt egy nagy mintatartományból nyert betűstatisztika, ami a frekvencia-analízis elengedhetetlen kelléke, illetve szóminták ismerete. A Caesar-kód mellett tanúskodik, ha a fejtés során rendszeresség tapasztalható a behelyettesítésben, így a munka jelentősen felgyorsulhat.
Ha eleve tudjuk, hogy ebben a kódolásban van rejtjelezve az üzenet, akkor a legegyszerűbb esetben az eltolásokat fokozatosan változtatva a szöveg a megfelelőhöz érve spontán dekódolódik.[3] Ez azonban hosszabb időt is vehet igénybe, illetve ha nem a teljes szöveget vizsgáljuk, esetleg fals pozitív találat is előfordulhat, ugyanis két különböző, de hasonló szerkezetű szónak lehet azonos kódolt alakja (természetesen különböző eltolásokkal). Ezt jelentősen lerövidíthetjük annak figyelembe vételével, hogy az egyes betűk, betűpárok eltérő sűrűséggel fordulnak elő egy szövegben. A helyes eltolás meglelésével a kódot feltörtnek nyilváníthatjuk.
Ha nincsen sejtésünk a kódolási rendszerről, a statisztikák erős eszközök, ugyanis az egyes helyettesítések rendszeres azonosságát kihasználva a Caesar-gyanú megerősíthető, innentől a fentebbi módszerekkel élhetünk. Ebben az esetben igazából nem annyira az egyes betűk, hanem a betűpárok nyújtanak felvilágosítást. Bármilyen eltolást is használjunk, esetleg keverést, a betűpárok sokkal inkább szisztematikusan fordulnak elő, még ha az egyéb karaktereket (szóköz, pont, vessző, egyéb) ki is veszi a rejtjelező a szövegből.
Megvalósítás[szerkesztés]
C programozási nyelvű példa[szerkesztés]
Az alábbi példa csak az angol ábécé betűivel működik korrekt módon.
void caesar(char* text, int offset) {
char letter;
while((letter = *text)) {
if(letter >= 'A' && letter <= 'Z')
*text = 65+(letter-65+offset)%26;
else if(letter >= 'a' && letter <= 'z')
*text = 97+(letter-97+offset)%26;
text++;
}
}
Java programozási nyelven[szerkesztés]
public class Caesar {
public static String caesarCode(String input, char offset) {
char[] out = input.toUpperCase().toCharArray();
for (int i = 0; i < out.length; i++) {
out[i] += offset - 'A';
if (out[i] > 'Z')
out[i] -= 'Z' - 'A' + 1;
}
return new String(out);
}
}
Források[szerkesztés]
- Simon Singh: Kódkönyv, Park Könyvkiadó 2001, ISBN 978-963-530-798-2
Jegyzetek[szerkesztés]
- ↑ Természetesen más számértékeket is tekinthetünk, a lényeg, hogy az egyes értékek különböző ekvivalencia-osztályokba essenek az ábécé hossza szerint osztva.
- ↑ Percy Bysshe Shelley: Ozymandiás - részlet (Tóth Árpád fordítása)
- ↑ Lényeges, hogy olyan eltolási rotációt válasszunk, ami relatív prím az ábécé hosszához, így ugyanis minden eltolás elő fog fordulni. Leggyakoribb az 1 lépés hosszú rotálás.
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a Caesar cipher című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
További információk[szerkesztés]
- Alice és Bob - 1. rész: Alice és Bob színrelép
- Caesar-rejtjel online kódolása és dekódolása Archiválva 2014. augusztus 8-i dátummal a Wayback Machine-ben
- Caesar-kódoló/visszafejtő




