Kiürített tartomány

A félvezetők fizikájában a kiürített tartomány, más nevén kiürített réteg egy dópolt félvezető anyag belsejében létrejövő szigetelő tulajdonságú réteget jelent, melyből a szabad töltéshordozók diffúzió vagy elektromos mező hatására távoztak.

A 'kiürített tartomány' elnevezés azon alapul, hogy egy elektromos áram vezetésére képes anyagban a szabad töltéshordozók eltávolításával, a réteg kiürítésével hozhatunk létre ilyen tartományt. A kiürült térrészben csupán az ionizált donor vagy akceptor szennyezők maradnak vissza. A kiürített tartomány jelenségeinek és tulajdonságainak feltárása vezet el bennünket a félvezető eszközök modern alkalmazásaihoz: a diódák, a félvezető tranzisztorok és a varikap diódák működése is a kiürített tartomány jelenségén alapul.

Létrejötte p–n átmenetben

Fent: p–n átmenet a diffúzió előtt; Lent: az egyensúly elérése után

Fent: lyuk- és elektronkoncentrációk az átmeneten; Alatta: töltéshordozók sűrűsége; Alatta: elektromos térerősség; Lent: elektromos potenciál

A p-n átmenetben, azaz egymással kapcsolatba hozott p típusú és n típusú félvezetők határfelületén a kiürített tartomány azonnal létrejön. A jelenség legegyszerűbben termikus egyensúlyban, vagy nyugalmi állapotban írható le: a rendszer makroszkopikus jellemzői ekkor időben változatlanok, a rendszer dinamikus egyensúlyban van.

A félvezetőben található töltéshordozók (elektronok és lyukak) koncentrációját két hatás befolyásolja. Az elektronok és lyukak diffúzió útján a kisebb koncentrációjú helyek irányába áramlanak hasonlóan ahhoz, ahogy a vízben egy csepp tinta szétterjed, míg teljesen el nem oszlik. P–n átmenetnek egy p típusú (lyukakban gazdag) és egy n típusú (elektronokban gazdag) félvezető találkozási határfelületét nevezzük. Az N-oldal elektronjai az átmenet létrehozásakor a P-oldal kisebb elektronkoncentrációja felé kezdenek terjedni, míg a P-oldali lyukakra ellentétes irányú diffúzió lesz jellemző.

Az eredetileg semleges töltésű anyagokban a töltések elmozdulása elektromos térerősséget gerjeszt. Az N-oldalon az elektronok koncentrációjának csökkenése és a lyukak koncentrációjának növekedése miatt pozitív, a P-oldalon hasonlóképpen negatív töltés alakul ki. Ez a töltéskülönbség a hajtóereje a töltéshordozók koncentrációját megszabó másik hatásnak, a driftáramnak. A létrejött elektromos tér az elektronokat a P-oldalról az N-oldal felé vonzza, míg a lyukakat az N-oldalról P-oldal felé mozdítja. A elektronok és lyukak driftárama éppen ellentétes ezek diffúziójának irányával. A két hatás dinamikus egyensúlya alakítja ki az anyag töltéshordozó-koncentrációját és alakítja ki a kiürített tartományt.

A kiürített tartomány mérete a p és n oldalakra kapcsolt feszültséggel befolyásolható.

1. Ha az N-oldalra a P-hez képest pozitív feszültséget alkalmazunk, a töltések diffúziójából eredő elektromos feszültség lecsökken, így a driftáram kisebb lesz. Az elektronok és a lyukak mélyebbre hatolnak diffúzióval az ellentétes dópolási polaritású oldalon, a driftáram lecsökken. A kiürített tartomány kiszélesedik és az átmeneten csak kis áramerősség tapasztalható az előfeszítés hatására. Ekkor záróirányú előfeszítésről beszélünk.
2. Ha ezzel ellentétes előfeszítést alkalmazunk (azaz az N-oldal negatív a P-oldalhoz képest), akkor a töltések diffúziójából eredő feszültség megnő, az anyagban a driftáram fog dominálni. Az elektronok és a lyukak nem tudnak nagyon eltávolodni a donor és akceptor iontörzsektől. A kiürített tartomány szélessége lecsökken és az átmeneten nagyobb áram haladhat át az előfeszítés hatására. Ezt nevezzük nyitóirányú előfeszítésnek.

Létrejötte MOS struktúrában

Metal–oxide–semiconductor structure on P-type silicon

Egy másik példa a kiürített tartomány jelenségén alapuló eszközre a MOSFET, melynek egy megvalósítása p típusú hordozóval a jobb oldali ábrán látható. Tegyük fel, hogy az eszköz p típusú tartománya eredetileg teljesen semleges töltésű, benne a lyukak pozitív töltése és az akceptorszerű szennyezők negatív töltése épp semlegesíti egymást. Ha a készülék kapuelektródáira pozitív töltést juttatunk, a létrejövő pozitív feszültség eltaszítja a lyukakat a félvezetőnek abból a tartományából, mely a kapuelektródához közel esik. A töltések az ábrán alul látható elektródán át távoznak és egy kiürített tartományt hagynak maguk után, mely mozgékony töltéshordozóban szegényebb, így szigetelő tulajdonságú. Ha a feszültséget növeljük, ez a tartomány kiszélesedik és egyre több lyuk távozik a félvezető anyagból.

A feszültség növelésével tehát növelhető a kiürített tartomány szélessége, azonban ennek határt szab az, hogy egy bizonyos feszültségnél inverziós réteg jelenik meg a félvezető anyag és a kapuelektróda közös felületén, mely a félvezető polaritásának megváltozását jelenti a felület kis környezetében, lehetővé téve az ellentétes töltések áramlását.

A kiürítés szélessége

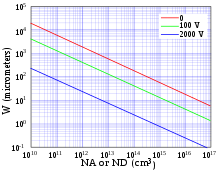
A kiürített tartomány méretét általában egy dimenzióval jellemezhetjük, ugyanis gyakoriak az olyan alkalmazások, ahol rétegstruktúrában jön létre a kiürítés, így az elektromos transzport szempontjából csak a tartomány szélessége érdekes.

p-n átmenetben

A kiürítés szélessége az alkalmazott előfeszítéstől és a szennyezők koncentrációjától függ.

A töltésmegmaradás értelmében egy semleges anyagban a töltések előjeles összege nulla. A félvezetőkben található töltésekre érvényes, hogy:

$n+N_{A}^{-}w_{P}=p+N_{D}^{+}w_{N}\,$,

ahol n és p a szabad elektronok illetve lyukak száma, $N_{D}^{+}$ és $N_{A}^{-}$ pedig rendre az ionizált donorok és akceptorokat jelöli.

Fordítás

Ez a szócikk részben vagy egészben a Depletion region című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Források

• Charles Kittel: Bevezetés a szilárdtest-fizikába. Budapest: Műszaki Könyvkiadó. 1981.  
• Sólyom, Jenő. Fundamentals of the Physics of Solids. Springer Berlin Heidelberg, 522. o.. DOI: 10.1007/978-3-540-72600-5 (2007). Hozzáférés ideje: 2017. május 19.