A matematikában a Csebisev-polinomok olyan ortogonális polinomsorozatok, melyek kapcsolatban állnak a De Moivre képlettel , és amelyeket rekurzív módon lehet definiálni. Nevüket Pafnutyij Lvovics Csebisev orosz matematikus után kapták. Általában különbséget tesznek elsőfajú Csebisev-polinomok (jelölés Tn ), illetve másodfajú Csebisev-polinomok között (jelölés Un ).
A Tn , és az Un Csebisev-polinomok n-ed fokúak, és bármelyik fajta Csebisev-polinomok sorozata polinomsorozatot alkot.
A Tn Csebisev-polinomok a lehető legnagyobb vezető együtthatóval rendelkeznek, figyelembe véve azt a tényt, hogy abszolút értékük a [-1,1] intervallumon kötve van az 1 által.
A Csebisev-polinomok fontos szerepet játszanak a közelítő módszerek elméletében, mivel az elsőfajú Csebisev-polinomok gyökeit, melyeket Csebisev-csomópontoknak is hívnak, csomópontokként használják a polinomiális interpolációnál. Az így kapott interpolációs polinom minimalizálja a Runge-hatásból származó problémát.
A differenciálegyenletek területén a Csebisev-differenciálegyenletek megoldásaként találunk rájuk:
(
1
−
x
2
)
y
″
−
x
y
′
+
n
2
y
=
0
{\displaystyle \left(1-x^{2}\right)y''-xy'+n^{2}y=0}
és
(
1
−
x
2
)
y
″
−
3
x
y
′
+
n
(
n
+
2
)
y
=
0
{\displaystyle \left(1-x^{2}\right)y''-3xy'+n(n+2)y=0}
Az első egyenletből kapjuk Tn -t, míg a másodikból Un -t. Ezek az egyenletek a Sturm-Liouville differenciálegyenletek speciális esetei.
Az első öt T típusú Csebisev-polinom ábrázolása Az első öt U típusú Csebisev-polinom ábrázolása Az elsőfajú Csebisev-polinomokat a következő rekurenciás összefüggés definiálja:
T
0
(
x
)
=
1
T
1
(
x
)
=
x
T
n
+
1
(
x
)
=
2
x
T
n
(
x
)
−
T
n
−
1
(
x
)
.
{\displaystyle {\begin{aligned}T_{0}(x)&=1\\T_{1}(x)&=x\\T_{n+1}(x)&=2xT_{n}(x)-T_{n-1}(x).\end{aligned}}}
A megszokott generátorfüggvény Tn -re:
∑
n
=
0
∞
T
n
(
x
)
t
n
=
1
−
t
x
1
−
2
t
x
+
t
2
;
{\displaystyle \sum _{n=0}^{\infty }T_{n}(x)t^{n}={\frac {1-tx}{1-2tx+t^{2}}};}
Az exponenciális generátorfüggvény:
∑
n
=
0
∞
T
n
(
x
)
t
n
n
!
=
1
2
(
e
(
x
−
x
2
−
1
)
t
+
e
(
x
+
x
2
−
1
)
t
)
=
e
t
x
cosh
(
t
x
2
−
1
)
.
{\displaystyle \sum _{n=0}^{\infty }T_{n}(x){\frac {t^{n}}{n!}}={\tfrac {1}{2}}\left(e^{\left(x-{\sqrt {x^{2}-1}}\right)t}+e^{\left(x+{\sqrt {x^{2}-1}}\right)t}\right)=e^{tx}\cosh \left(t{\sqrt {x^{2}-1}}\right).}
A kétdimenziós potenciálelmélet területén releváns generátorfüggvény:
∑
n
=
1
∞
T
n
(
x
)
t
n
n
=
ln
1
1
−
2
t
x
+
t
2
.
{\displaystyle \sum \limits _{n=1}^{\infty }T_{n}(x){\frac {t^{n}}{n}}=\ln {\frac {1}{\sqrt {1-2tx+t^{2}}}}.}
A másodfajú Csebisev-polinomokat a következő rekurenciás összefüggés definiálja:
U
0
(
x
)
=
1
U
1
(
x
)
=
2
x
U
n
+
1
(
x
)
=
2
x
U
n
(
x
)
−
U
n
−
1
(
x
)
.
{\displaystyle {\begin{aligned}U_{0}(x)&=1\\U_{1}(x)&=2x\\U_{n+1}(x)&=2xU_{n}(x)-U_{n-1}(x).\end{aligned}}}
A megszokott generátorfüggvény Un -re:
∑
n
=
0
∞
U
n
(
x
)
t
n
=
1
1
−
2
t
x
+
t
2
;
{\displaystyle \sum _{n=0}^{\infty }U_{n}(x)t^{n}={\frac {1}{1-2tx+t^{2}}};}
Az exponenciális generátorfüggvény:
∑
n
=
0
∞
U
n
(
x
)
t
n
n
!
=
e
t
x
(
cosh
(
t
x
2
−
1
)
+
x
x
2
−
1
sinh
(
t
x
2
−
1
)
)
.
{\displaystyle \sum _{n=0}^{\infty }U_{n}(x){\frac {t^{n}}{n!}}=e^{tx}\left(\cosh \left(t{\sqrt {x^{2}-1}}\right)+{\frac {x}{\sqrt {x^{2}-1}}}\sinh \left(t{\sqrt {x^{2}-1}}\right)\right).}
Kapcsolatok az első- illetve másodfajú Csebisev-polinomok között [ szerkesztés ] Az első- illetve másodfajú Csebisev-polinomok megfelelnek a Lucas sorozat egy kiegészítő párjának Ṽn (P ,Q )Ũn (P ,Q )P = 2x Q = 1
U
~
n
(
2
x
,
1
)
=
U
n
−
1
(
x
)
,
V
~
n
(
2
x
,
1
)
=
2
⋅
T
n
(
x
)
.
{\displaystyle {\begin{aligned}{\tilde {U}}_{n}(2x,1)&=U_{n-1}(x),\\{\tilde {V}}_{n}(2x,1)&=2\cdot T_{n}(x).\end{aligned}}}
Két kölcsönös rekurenciás összefüggést is kielégítenek:
T
n
+
1
(
x
)
=
x
T
n
(
x
)
−
(
1
−
x
2
)
U
n
−
1
(
x
)
,
U
n
(
x
)
=
x
U
n
−
1
(
x
)
+
T
n
(
x
)
.
{\displaystyle {\begin{aligned}T_{n+1}(x)&=xT_{n}(x)-(1-x^{2})U_{n-1}(x),\\U_{n}(x)&=xU_{n-1}(x)+T_{n}(x).\end{aligned}}}
Az első- illetve másodfajú Csebisevpolinomokat a következő összefüggések is összekapcsolják:
T
n
(
x
)
=
1
2
(
U
n
(
x
)
−
U
n
−
2
(
x
)
)
.
T
n
(
x
)
=
U
n
(
x
)
−
x
U
n
−
1
(
x
)
.
U
n
(
x
)
=
2
∑
odd
j
n
T
j
(
x
)
páratlan
n
.
U
n
(
x
)
=
2
∑
even
j
n
T
j
(
x
)
−
1
páros
n
.
{\displaystyle {\begin{aligned}T_{n}(x)&={\tfrac {1}{2}}{\big (}U_{n}(x)-U_{n-2}(x){\big )}.&&\\T_{n}(x)&=U_{n}(x)-x\,U_{n-1}(x).&&\\U_{n}(x)&=2\sum _{{\text{odd }}j}^{n}T_{j}(x)&&{\text{páratlan }}n.\\U_{n}(x)&=2\sum _{{\text{even }}j}^{n}T_{j}(x)-1&&{\text{páros }}n.\end{aligned}}}
A Csebisev-polinomok meghatározásának különböző megközelítései különböző explicit kifejezésekhez vezetnek, mint például:
T
n
(
x
)
=
{
cos
(
n
arccos
x
)
|
x
|
≤
1
1
2
(
(
x
−
x
2
−
1
)
n
+
(
x
+
x
2
−
1
)
n
)
|
x
|
≥
1
=
{
cos
(
n
arccos
x
)
−
1
≤
x
≤
1
cosh
(
n
arcosh
x
)
1
≤
x
(
−
1
)
n
cosh
(
n
arcosh
(
−
x
)
)
x
≤
−
1
T
n
(
x
)
=
∑
k
=
0
⌊
n
2
⌋
(
n
2
k
)
(
x
2
−
1
)
k
x
n
−
2
k
=
x
n
∑
k
=
0
⌊
n
2
⌋
(
n
2
k
)
(
1
−
x
−
2
)
k
=
n
2
∑
k
=
0
⌊
n
2
⌋
(
−
1
)
k
(
n
−
k
−
1
)
!
k
!
(
n
−
2
k
)
!
(
2
x
)
n
−
2
k
n
>
0
=
n
∑
k
=
0
n
(
−
2
)
k
(
n
+
k
−
1
)
!
(
n
−
k
)
!
(
2
k
)
!
(
1
−
x
)
k
n
>
0
=
2
F
1
(
−
n
,
n
;
1
2
;
1
2
(
1
−
x
)
)
{\displaystyle {\begin{aligned}T_{n}(x)&={\begin{cases}\cos(n\arccos x)&|x|\leq 1\\\\{\frac {1}{2}}{\bigg (}{\Big (}x-{\sqrt {x^{2}-1}}{\Big )}^{n}+{\Big (}x+{\sqrt {x^{2}-1}}{\Big )}^{n}{\bigg )}\qquad &|x|\geq 1\\\end{cases}}\\\\\\&={\begin{cases}\cos(n\arccos x)&-1\leq x\leq 1\\\\\cosh(n\operatorname {arcosh} x)&1\leq x\\(-1)^{n}\cosh {\big (}n\operatorname {arcosh} (-x){\big )}\qquad &x\leq -1\\\end{cases}}\\\\\\T_{n}(x)&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {n}{2k}}\left(x^{2}-1\right)^{k}x^{n-2k}\\&=x^{n}\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {n}{2k}}\left(1-x^{-2}\right)^{k}\\&={\tfrac {n}{2}}\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }(-1)^{k}{\frac {(n-k-1)!}{k!(n-2k)!}}~(2x)^{n-2k}\qquad n>0\\&=n\sum _{k=0}^{n}(-2)^{k}{\frac {(n+k-1)!}{(n-k)!(2k)!}}(1-x)^{k}\qquad n>0\\&={}_{2}F_{1}\left(-n,n;{\tfrac {1}{2}};{\tfrac {1}{2}}(1-x)\right)\\\end{aligned}}}
x
n
=
2
1
−
n
∑
′
j
=
0
,
n
−
j
páros
n
(
n
n
−
j
2
)
T
j
(
x
)
,
{\displaystyle x^{n}=2^{1-n}\mathop {{\sum }'} _{j=0,n-j{\text{ páros}}}^{n}{\binom {n}{\tfrac {n-j}{2}}}T_{j}(x),}
ahol a szummajel alapja azt jelzi, hogy a j = 0
U
n
(
x
)
=
(
x
+
x
2
−
1
)
n
+
1
−
(
x
−
x
2
−
1
)
n
+
1
2
x
2
−
1
=
∑
k
=
0
⌊
n
2
⌋
(
n
+
1
2
k
+
1
)
(
x
2
−
1
)
k
x
n
−
2
k
=
x
n
∑
k
=
0
⌊
n
2
⌋
(
n
+
1
2
k
+
1
)
(
1
−
x
−
2
)
k
=
∑
k
=
0
⌊
n
2
⌋
(
2
k
−
(
n
+
1
)
k
)
(
2
x
)
n
−
2
k
n
>
0
=
∑
k
=
0
⌊
n
2
⌋
(
−
1
)
k
(
n
−
k
k
)
(
2
x
)
n
−
2
k
n
>
0
=
∑
k
=
0
n
(
−
2
)
k
(
n
+
k
+
1
)
!
(
n
−
k
)
!
(
2
k
+
1
)
!
(
1
−
x
)
k
n
>
0
=
(
n
+
1
)
2
F
1
(
−
n
,
n
+
2
;
3
2
;
1
2
(
1
−
x
)
)
{\displaystyle {\begin{aligned}U_{n}(x)&={\frac {\left(x+{\sqrt {x^{2}-1}}\right)^{n+1}-\left(x-{\sqrt {x^{2}-1}}\right)^{n+1}}{2{\sqrt {x^{2}-1}}}}\\&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {n+1}{2k+1}}\left(x^{2}-1\right)^{k}x^{n-2k}\\&=x^{n}\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {n+1}{2k+1}}\left(1-x^{-2}\right)^{k}\\&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {2k-(n+1)}{k}}~(2x)^{n-2k}&&n>0\\&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }(-1)^{k}{\binom {n-k}{k}}~(2x)^{n-2k}&&n>0\\&=\sum _{k=0}^{n}(-2)^{k}{\frac {(n+k+1)!}{(n-k)!(2k+1)!}}(1-x)^{k}&&n>0\\&=(n+1)\ {}_{2}F_{1}\left(-n,n+2;{\tfrac {3}{2}};{\tfrac {1}{2}}(1-x)\right)\\\end{aligned}}}
ahol 2 F 1
Az első néhány elsőfajú Csebisev-polinom a −1 < x < 1 intervallumon: T 0 T 1 T 2 T 3 T 4 T 5 Az első néhány elsőfajú Csebisev-polinom A028297
T
0
(
x
)
=
1
T
1
(
x
)
=
x
T
2
(
x
)
=
2
x
2
−
1
T
3
(
x
)
=
4
x
3
−
3
x
T
4
(
x
)
=
8
x
4
−
8
x
2
+
1
T
5
(
x
)
=
16
x
5
−
20
x
3
+
5
x
T
6
(
x
)
=
32
x
6
−
48
x
4
+
18
x
2
−
1
T
7
(
x
)
=
64
x
7
−
112
x
5
+
56
x
3
−
7
x
T
8
(
x
)
=
128
x
8
−
256
x
6
+
160
x
4
−
32
x
2
+
1
T
9
(
x
)
=
256
x
9
−
576
x
7
+
432
x
5
−
120
x
3
+
9
x
T
10
(
x
)
=
512
x
10
−
1280
x
8
+
1120
x
6
−
400
x
4
+
50
x
2
−
1
T
11
(
x
)
=
1024
x
11
−
2816
x
9
+
2816
x
7
−
1232
x
5
+
220
x
3
−
11
x
{\displaystyle {\begin{aligned}T_{0}(x)&=1\\T_{1}(x)&=x\\T_{2}(x)&=2x^{2}-1\\T_{3}(x)&=4x^{3}-3x\\T_{4}(x)&=8x^{4}-8x^{2}+1\\T_{5}(x)&=16x^{5}-20x^{3}+5x\\T_{6}(x)&=32x^{6}-48x^{4}+18x^{2}-1\\T_{7}(x)&=64x^{7}-112x^{5}+56x^{3}-7x\\T_{8}(x)&=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1\\T_{9}(x)&=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x\\T_{10}(x)&=512x^{10}-1280x^{8}+1120x^{6}-400x^{4}+50x^{2}-1\\T_{11}(x)&=1024x^{11}-2816x^{9}+2816x^{7}-1232x^{5}+220x^{3}-11x\end{aligned}}}
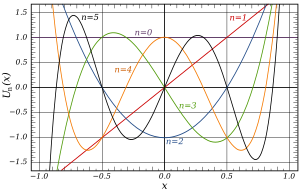
Az első néhány másodfajú Csebisev-polinom a −1 < x < 1 intervallumon: U 0 U 1 U 2 U 3 U 4 U 5 U n n + 1U n n + 1)(−1)n Az első néhány másodfajú Csebisev-polinom A053117
U
0
(
x
)
=
1
U
1
(
x
)
=
2
x
U
2
(
x
)
=
4
x
2
−
1
U
3
(
x
)
=
8
x
3
−
4
x
U
4
(
x
)
=
16
x
4
−
12
x
2
+
1
U
5
(
x
)
=
32
x
5
−
32
x
3
+
6
x
U
6
(
x
)
=
64
x
6
−
80
x
4
+
24
x
2
−
1
U
7
(
x
)
=
128
x
7
−
192
x
5
+
80
x
3
−
8
x
U
8
(
x
)
=
256
x
8
−
448
x
6
+
240
x
4
−
40
x
2
+
1
U
9
(
x
)
=
512
x
9
−
1024
x
7
+
672
x
5
−
160
x
3
+
10
x
{\displaystyle {\begin{aligned}U_{0}(x)&=1\\U_{1}(x)&=2x\\U_{2}(x)&=4x^{2}-1\\U_{3}(x)&=8x^{3}-4x\\U_{4}(x)&=16x^{4}-12x^{2}+1\\U_{5}(x)&=32x^{5}-32x^{3}+6x\\U_{6}(x)&=64x^{6}-80x^{4}+24x^{2}-1\\U_{7}(x)&=128x^{7}-192x^{5}+80x^{3}-8x\\U_{8}(x)&=256x^{8}-448x^{6}+240x^{4}-40x^{2}+1\\U_{9}(x)&=512x^{9}-1024x^{7}+672x^{5}-160x^{3}+10x\end{aligned}}}
(1995) „A Note on Some Peculiar Nonlinear Extremal Phenomena of the Chebyshev Polynomials”. Proceedings of the Edinburgh Mathematical Society 38 , 343–355. o. DOI :10.1017/S001309150001912X . (1964) „The evaluation and estimation of the coefficients in the Chebyshev Series expansion of a function ”. Math. Comp. 18 , 274–284. o. DOI :10.1090/S0025-5718-1964-0166903-7 . (1994) „An Extremal Problem For Polynomials ”. Proceedings of the American Mathematical Society 122 , 191–193. o. DOI :10.1090/S0002-9939-1994-1207536-1 . (2001) „Chebyshev's approximation algorithms and applications”. Comp. Math. Applic. 41 , 433–445. o. (1984) „Some properties and applications of Chebyshev polynomial and rational approximation”. Lect. Not. Math. 1105 , 27–48. o. DOI :10.1007/BFb0072398 . Chebyshev Polynomials (2006) „Chebyshev series expansion of inverse polynomials”. J. Comput. Appl. Math. 196 , 596–607. o. DOI :10.1016/j.cam.2005.10.013 . Remes, Eugene: On an Extremal Property of Chebyshev Polynomials (1976) „Converting interpolation series into Chebyshev Series by Recurrence Formulas ”. Math. Comp. 30 , 295–302. o. DOI :10.1090/S0025-5718-1976-0395159-3 . (1969) „The Solution of integral equations in Chebyshev series ”. Math. Comput. 23 , 837–844. o. DOI :10.1090/S0025-5718-1969-0260224-4 . (1966) „Algorithm 277, Computation of Chebyshev series coefficients”. Comm. ACM 9 , 86–87. o. DOI :10.1145/365170.365195 . 


![]() A028297
A028297
![]() A053117
A053117

















