Cage (gráfelmélet)
| (3-6)-cage | |
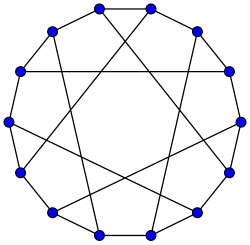 | |
| Heawood-gráf | |
| Névadó | Percy John Heawood |
| Csúcsok száma | 14 |
| Élek száma | 21 |
| Sugár | 3 |
| Átmérő | 3 |
| Derékbőség | 6 |
| Kromatikus szám | 2 |
| Élkromatikus szám | 3 |
| Automorfizmusok | 336 |
| Génusz | 1 |
Azokat a speciális gráfokat nevezzük cage-nek (kalitkának) amelyek reguláris gráfok, és egy rögzített girth (a legrövidebb kör a gráfban) mellett a lehető legkevesebb csúcsuk van.
Tehát az (r,g)-cage-k speciális elemei annak a gráfcsaládnak amik azokból a gráfokból állnak ahol minden fokszám r és a gráfban található legrövidebb kör hossza g. Minden r ≥ 2 és g ≥ 3 esetén létezik olyan gráf ami r-reguláris és amiben a girth éppen g. Mivel ezek közül a legkevesebb csúccsal rendelkezőket hívjuk (r,g)-cage gráfoknak, ezért ezekben az esetekben létezik is (r,g)-cage. Rögzített r és g esetén létezhet több (r,g)-cage is, például három nem izomorf (3,10)-cage létezik.
Ismert cage-ek[szerkesztés]
r=1 esetén egy gráf nem tartalmazhat kört, így semmilyen véges g esetén nincs (1,g)-cage.
r=2 esetén egy gráf csak diszjunkt körök uniója lehet. Ezekben az esetekben a girth nyilvánvalóan a legkisebb kör hossza. Mivel azokat a gráfokat nevezzük cage-nek, amik ilyen feltételek mellett a lehető legkevesebb csúcsot tartalmazzák, ezért a (2,g)-cage gráfok pontosan a g hosszú körök.
r=3 esetén már számos cage-t ismerünk, az első néhány:[1]
- (3,3)-cage a K4 teljes gráf
- (3,4)-cage a K4,4 teljes páros gráf
- (3,5)-cage a Petersen-gráf
- (3,6)-cage a Heawood-gráf (melynek a tóruszba való beágyazása a Szilassi-poliéder)
- (3,7)-cage a McGee-gráf
- (3,8)-cage az illeszkedési gráf (másik nevén a Tutte 8-cage)
Tetszőleges r esetén:[2]
- Az (r,3)-cage a Kr+1 teljes gráf
- Az (r,4)-cage a Kr,r teljes páros gráf
Jegyzetek[szerkesztés]
- ↑ az ismert 3-reguláris cage gráfok g=32 ig. [2008. október 30-i dátummal az eredetiből archiválva]. (Hozzáférés: 2009. május 14.)
- ↑ A jelenleg ismert cage gráfok, és a nem ismertek csúcsszámára vonatkozó becslések [1] Archiválva 2009. január 25-i dátummal a Wayback Machine-ben
Források[szerkesztés]
- Wolfram MathWorld Cage Graph
- Brouwer, Andries E. Cage
