Körülfordulási szám
A körülfordulási szám, más néven index görbék topológiai invariánsa, ami a komplex analízisben is meghatározó.
Informálisan, a körülfordulási szám azt adja meg, hogy az adott görbe hányszor kerül meg egy adott pontot. A megkerülést előjelesen kell értelmezni, ahol az óramutató járásával ellentétes irány pozitív, az óramutató szerinti negatív.
Definíció[szerkesztés]
Komplex számsíkba ágyazott zárt görbe esetén a körülfordulási szám értelmezhető a következőképpen: Legyen zárt görbe a síkban, és komplex szám, ami nincs rajta a görbén! Ekkor körüli körülfordulási száma
A körülfordulási szám mindig egész, és értelmezhető topológiai eszközökkel is.
| Körülfordulási szám = 1 | Körülfordulási szám = -1 | Körülfordulási szám = 0 | Körülfordulási szám = 1 | Körülfordulási szám = 2 |
|---|---|---|---|---|
Kiszámítása[szerkesztés]

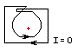
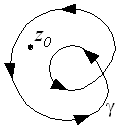
Nem mindig alkalmazható az intuitív kiszámítási mód, hogy a pozitív forgásirányú körüljárások számából levonjuk a negatív forgásirányú körüljárások számát.
A képlet levezetéséhez tekintsük az egységkört!
Jelölje a körvonal belsejét! Ekkor intuitívan minden és minden komplex számra. Ez utóbbi a Cauchy-féle integráltétel és a definíció következménye. Most legyen
Teljesül, hogy
A deriválás és az integrálás felcserélésével
és mivel az az integrandus primitív függvénye, . Továbbá összefüggősége miatt minden esetén.
Alkalmazás a komplex analízisben[szerkesztés]
A körülfordulási számot legtöbbször görbe menti integrálok kiszámítására használják. Legyen
meromorf, és szingularitásait jelölje ! Ekkor a reziduumtétel miatt integrálja egy, a szingularitásokat elkerülő görbe menti integrálja
Algoritmus[szerkesztés]
Az algoritmikus geometriában a körülfordulási számot arra használják, hogy eldöntsék, hogy egy pont egy nem egyszerű sokszögön belül van-e. Egyszerű sokszögek esetén az eljárás a páros-páratlan szabályra egyszerűsíthető.
Sokszögekre általános esetben a következő algoritmus alkalmazható:
- 1. Keresünk egy félegyenest, ami nem megy át a sokszög csúcsain.
- 2. Legyen
- 3. A félegyenes és a sokszögvonal összes metszéspontjára:
- Ha az elmetszett él jobbról balra van irányítva, azaz a pont az él bal oldalán van, akkor növeljük -t eggyel.
- Ha az elmetszett él balról jobbra van irányítva, azaz a pont az él jobb oldalán van, akkor csökkentjük -t eggyel.
- 4. Miután az összes elmetszett élt végignéztük, éppen a körülfordulási szám. Ha ez nulla, akkor a pont a sokszögön kívül van, különben belül.
Hasonlóan lehet nem egyenes szakaszokból álló zárt görbékre elvégezni a vizsgálatot, de ekkor nem adódik olyan triviálisan a metszéspontok vizsgálata.
Magasabb dimenziós sokaságokon[szerkesztés]
Magasabb dimenziós sokaságokra Nyikolaj Nyikolajevics Bogoljubov általánosította a körülfordulási számot. A Stokes-tétel alkalmazásával a pontra kapjuk, hogy
ahol egységgömb -ben, és az dimenziós sokaság, amin integrálunk.
Források[szerkesztés]
- Eberhard Freitag, Rolf Busam: Funktionentheorie 1. Springer-Verlag, Berlin, ISBN 3-540-67641-4
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Windungszahl című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.









![{\displaystyle \gamma \colon [0,2\pi ]\to \mathbb {C} ,t\mapsto e^{\mathrm {i} t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeeb7c15dee0fa41c6fa693af82b40b45f6deec5)





















