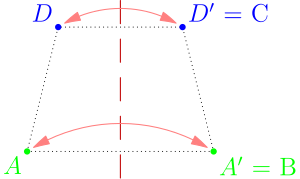
Húrtrapéz
Húrtrapézoknak azokat a négyszögeket hívjuk, amelyeknek van olyan szimmetriatengelyük, amelyre nem illeszkedik egy csúcsuk sem.[1][2] Húrtrapézt a szimmetriatengelyére tükrözve két-két csúcs éppen helyet cserél: a szimmetriatengely a húrtrapéz két (egymással szemközti) oldalának közös felezőmerőlegese, a másik két (egymással szintén szemközti oldal) pedig egymás tükörképe.
A húrtrapézok tehát a tengelyesen szimmetrikus négyszögek egy részhalmazát alkotják. Nemcsak húrtrapézok lehetnek tengelyesen szimmetrikus négyszögek: négyszög lehet úgy is tengelyesen szimmetrikus, hogy két (egymással szembelévő) csúcsuk illeszkedik a szimmetriatengelyre (így saját magának tükörképe), a másik két (egymással szintén szemközti) csúcs pedig épp egymás tükörképe. A tengelyesen szimmetrikus négyszögeknek ezt a „másik” családját deltoidoknak nevezzük. A deltoidok tehát szintén tengelyesen szimmetrikus négyszögek: van olyan szimmetriatengelyük, amelyre illeszkedik csúcsuk (kettő is).
Tengelyesen szimmetrikus négyszög csak húrtrapéz vagy deltoid lehet, de a két tulajdonság nem zárja ki egymást, hiszen négyszögnek több szimmetriatengelye is lehet: kettő, (három nem!) vagy négy. Négy szimmetriatengelye éppen a négyzeteknek van (kettő „átlósan”). Minden négyzet húrnégyszög és egyúttal deltoid is (a két „átlós” szimmetriatengelyére „nézve” deltoid, a másik kettőre „nézve” pedig húrtrapéz). Csak négyzetek tekinthetők egyszerre húrtrapéznak és deltoidnak is.
A húrtrapézokra sok érdekes, nemtriviális (nem magától értetődő) összefüggés teljesül, tehát ezt a fogalmat érdemes bevezetni. Példa ilyen összefüggésre: minden húrtrapéz köré írható kör, vagyis tetszőleges húrtrapézhoz található olyan kör, amelyre mind a négy csúcsa illeszkedik.
Egyenértékű meghatározások[szerkesztés]
Ez előbbi fenti összefüggés „fordítva” nem igaz, vagyis nem minden köré írt körrel rendelkező négyszög húrtrapéz is egyben. Azonban könnyű példát mondani olyan összefüggésekre is, amelyek megfordíthatóak. Például: Minden húrtrapézra igaz az alábbi két tulajdonság egyszerre:
- az egyik oldaluk párhuzamos a vele szemközti oldallal, vagyis van legalább egy párhuzamos oldalpárjuk; és
- írható köréjük kör, vagyis van olyan kör, amelyre mind a négy csúcsuk illeszkedik.
Tehát, ha egy négyszög húrtrapéz, akkor egyúttal trapéz is (első tulajdonság), és egyben húrnégyszög is (második tulajdonság).
Ez az összefüggés „fordítva” is igaz: ha tudjuk hogy egy négyszögre igaz a fenti 1. és 2. tulajdonság is (vagyis a négyszög trapéz is és húrnégyszög is), akkor az csakis olyan négyszög lehet, amely e cikk nyitó mondatában említett tulajdonságokkal rendelkezik (vagyis húrtrapéz).
Mindez azt jelenti, hogy ha az összes négyszög halmazából részhalmazt képzünk úgy, hogy a részhalmazba éppen azokat a négyszögeket vesszük be, amelyekre egyszerre teljesül a fenti 1. és 2. tulajdonság (tehát párhuzamos oldalpárjuk is van, és körülírt körük is, szóval egyszerre trapézok és húrnégyszögek is), akkor ugyanazt a részhalmazt kapjuk, mintha e cikk nyitó mondatában leírt tulajdonság alapján végeztük volna a kiválogatást.
Sok más példát is találhatunk olyan összefüggésekre, amelyek szintén „megfordíthatóak”. Pl. minden húrtrapéznak van két egyenlő, egymással szomszédos szöge, és a másik két egymással szomszédos szögpárjuk is egyenlő egymással. Ez a tulajdonság is megfordítható: minden olyan négyszög, amelynek van két-két egyenlő szomszédos szöge, egyúttal húrtrapéz is.
A „megfordítható” összefüggések léte azt jelenti, hogy valójában a húrtrapéz „tulajdonságot” többféle, egymással egyenértékű (ekvivalens) definícióval is megfogalmazhatjuk, vagyis több, egymással egyenértékű tulajdonság közül bármelyik alapján eldönthetjük, egy négyszög húrtrapéz-e vagy sem:
- Húrtrapézoknak nevezzük azokat a négyszögeket, amelyeknek van csúcsra nem illeszkedő szimmetriatengelyük.
- Húrtrapézoknak nevezzük azokat a tengelyesen szimmetrikus négyszögeket, amelyek csúcsai közül kettő-kettő épp egymás tükörképe.
- Húrtrapézoknak nevezzük azokat a négyszögeket, amelyek húrnégyszögek és egyúttal trapézok is. (Azaz van párhuzamos oldalpárjuk, és kör is írható köréjük).
- Húrtrapézoknak nevezzük azokat a négyszögeket, amelyeknek két-két szomszédos szögük egyenlő.[1][3] Azokat az oldalakat, amelyeken az egyenlő szögek fekszenek, alapoknak nevezzük, a másik két oldalt száraknak.
- …
- …
- …
Ennek megfelelően a húrtrapézok fogalmát ezek közül az egymással ekvivalens tulajdonságok közül bármelyikkel definiálhatjuk. Mindegy, hogy a fenti 1., 2., 3., 4., vagy más ekvivalens meghatározás alapján döntjük el a egy négyszögről, hogy húrtrapéz-e vagy sem: mindegyik definíció az összes négyszög halmazából ugyanazt a részhalmazt jelöli ki. Mindez azonban egyáltalán nem nyilvánvaló: geometriai bizonyítások igazolják azt, hogy különbözőképpen felépített meghatározások, tulajdonságok valójában ugyanazt a részhalmazt jelölik ki az összes lehetséges négyszögek halmazából.
Ennek megfelelően, sok szakmunka, matematikai könyv a „húrtrapéz” fogalmát máshogy definiálja, mint ennek a cikknek a nyitó mondata, vagyis az itt olvasható meghatározás helyett egy ezzel egyenértékű másik meghatározást használ. Sőt, a „húrtrapéz” kifejezés helyett is más kifejezést olvasható sok műben. Van könyv, amely a „szimmetrikus trapéz” kifejezést használja, másutt „egyenlő szárú trapéz” kifejezés szerepel, sőt eseti szóhasználattal az „egyenlő szögű trapéz” kifejezés is előfordul.[3] Mindezek alatt a fogalmak alatt ugyanazt kell érteni abban az értelemben, hogy az összes négyszögek halmazából mindezek a szakszavak ugyanazt a részhalmazt nevezik meg.

Hivatkozások[szerkesztés]
- ↑ a b Csordás Mihály & Konfár László & Kothenecz Jánosné & Kozmáné Jakab Ágnes & Pintér Klára & Vincze Istvánné (2013): Sokszínű matematika 6 (tankönyv). Szeged: Mozaik Kiadó. ISBN 978 963 697 523 4. 145. oldal.
- ↑ Kosztolányi József & Kovács István & Pintér Klára & Urbán János & Vincze István (2010): Sokszínű matematika 9 (tankönyv). Szeged: Mozaik Kiadó. ISBN 978 963 697 347 6. 208. oldal.
- ↑ a b Hajós György „Bevezetés a geometriába” c. könyvében ezt a tulajdonságot választja definícióként. A tárgyalásmód szóhasználata arra utal, hogy a négyszögeket egyfajta "dualitás" szerinti rendszerezés mentén mutatja be: ennek alapján a húrtrapéz tulajdonságait a deltoidéval érdemes egybevetni (ahol előbbinek a definíciója: "két-két szomszédos szöge egyenlő", utóbbinak a definíciója pedig: "két-két szomszédos oldala egyenlő"). A "dualitás" szerinti tárgyalásmód nyomon követhető Csahóczi Erzsébet & Csatár Katalin & Kovács Csongorné & Morvai Éva & Széplaki Györgyné & Szeredi Éva : Matematika 6. tankönyvében is (II. kötet, Apáczai Kiadó, 2009, 17--19. o.).