Élgráf

A Wikipédiából, a szabad enciklopédiából

A gráfelmélet területén egy irányítatlan G gráfhoz tartozó élgráf egy olyan L(G) gráf, amely a G gráf élei közötti szomszédsági viszonyokat reprezentálja. Röviden élgráf az a gráf, amiben a csúcspontok az eredeti gráf élei, és két csúcs akkor van összekötve, ha az eredeti gráfban a két élnek volt közös végpontja. Maga az élgráf (line graph) kifejezés (Harary & Norman 1960)-ból jön, bár a konstrukciót előtte (Whitney 1932) és (Krausz 1943) is használta.[1] Az élgráf egyéb megnevezései közé tartozik a covering graph (burkológráf), a derivative (származtatott gráf), az edge-to-vertex dual (él–csúcs-duális), a conjugate (konjugált gráf), a representative graph (reprezentatív gráf) és a ϑ-obrazom,[2] továbbá az edge graph (élgráf), az interchange graph (cseregráf), az adjoint graph és a derived graph.[3]

Hassler Whitney (1932) igazolta, hogy egy kivételes esettől eltekintve az összefüggő gráfok szerkezete visszanyerhető élgráfjuk ismeretében.[4] Az élgráfok számos tulajdonsága közvetlenül az eredeti gráf csúcsainak élekké konvertálására vezethető vissza, és Whitney tétele értelmében ez az átalakítás visszirányban is végrehajtható. Az élgráfok karommentesek, a páros gráfok élgráfjai pedig perfekt gráfok. Az élgráfokat kilenc tiltott részgráf jellemzi, és lineáris idő alatt felismerhetők.

Az élgráfok számos általánosítását tanulmányozták már, köztük az élgráfok élgráfjait, a multigráfok élgráfjait, a hipergráfok élgráfjait és a súlyozott gráfok élgráfjait.

Formális definíció[szerkesztés]

Vegyünk egy G gráfot, ekkor L(G) élgráfja olyan gráf, amire a következők teljesülnek:

  • minden L(G)-ben szereplő csúcs megfelel egy G-ben lévő élnek;
  • két csúcs L(G)-ben akkor és csak akkor szomszédos, ha a nekik megfelelő éleknek van közös végpontjuk G-ben.

Tehát az élgráf G éleinek metszetgráfja , ami minden élet két végpontjával reprezentál.[3]

Példa[szerkesztés]

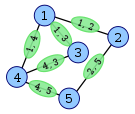
A következő ábrákon egy gráf látható (bal oldal, kék csúcsok) a hozzá tartozó élgráfjával (jobb oldal, zöld csúcsok). Az élgráf minden csúcsa meg van címkézve az eredeti gráf hozzá tartozó éle szerint. Például a jobb oldali 1,3 címkéjű zöld csúcs a bal oldalon az 1-es és 3-as kék színű csúcsokat összekötő élet jelképezi. A zöld 1,3 csúcs szomszédos három másik zöld csúccsal: az 1,4-gyel és 1,2-vel (mindkettő az 1-es csúcsból kiinduló él) és a 4,3 (a 3 végű él a kék gráfban).

  • G gráf
    G gráf
  • A G gráf éleiből konstruált L(G) csúcsai
    A G gráf éleiből konstruált L(G) csúcsai
  • Az L(G)-hez hozzáadott élek
    Az L(G)-hez hozzáadott élek
  • Az L(G) élgráf
    Az L(G) élgráf

Tulajdonságok[szerkesztés]

Az alapját képező gráf tulajdonságainak változásai[szerkesztés]

A G gráf az éleinek szomszédosságán alapuló tulajdonságai átalakulnak az L(G) csúcsok szomszédosságán alapuló tulajdonságaiba. Például G egy párosítása olyan élek halmaza, melyek közül páronként egyik sem szomszédos; ez L(G)-ben megfelel csúcsok olyan halmazának, melyben semelyik két csúcs nem szomszédos, tehát a csúcsok független halmazt alkotnak.[5]

Így aztán:

  • Egy összefüggő gráf élgráfja is összefüggő. Ha G összefüggő, tartalmaz bármely két élét összekötő sétát, ami az L(G) élgráf bármely két csúcsát összekötő sétává alakul. Azonban található olyan, izolált csúcsokkal rendelkező G gráf, aminek élgráfja mégis összefüggő.[6]
  • Egy élgráfnak akkor és csak akkor létezik elvágó pontja (artikulációs pontja), ha az eredeti gráf tartalmaz olyan elválasztó élt (hidat), melynek egyik végpontja sem elsőfokú.[3]
  • Egy n csúccsal és m éllel rendelkező G gráfhoz tartozó L(G) élgráf csúcsainak száma m, éleinek száma pedig G csúcsai fokszámának négyzetösszegének fele mínusz m.[7]
  • Egy élgráf maximális független halmaza az eredeti gráf maximális párosításának feleltethető meg. Mivel a maximális párosítások polinomiális időben megtalálhatók, ugyanez a helyzet az élgráfok maximális független halmazaival is, annak ellenére, hogy általános gráfoknál a maximális független halmaz keresése nehezebb probléma.[5]
  • A G gráf élkromatikus száma megegyezik L(G) élgráfjának (csúcs)kromatikus számával.[8]
  • Egy éltranzitív gráf élgráfja csúcstranzitív. Ennek a tulajdonságnak a segítségével generálhatók a Petersen-gráfhoz hasonló olyan gráfcsaládok, melyek csúcstranzitívak, de nem Cayley-gráfok: ha a G éltranzitív gráf legalább öt csúcsból áll, nem páros és vannak páratlan fokszámú csúcsai, akkor L(G) egy csúcstranzitív nem-Cayley-gráf.[9]
  • Ha G gráfnak van Euler-köre, tehát olyan összefüggő gráf, aminek minden csúcsából páros számú él indul ki, akkor G élgráfja Hamilton-gráf. Azonban nem minden Hamilton-utat tartalmazó élgráf származtatható Euler-kört tartalmazó gráfból; minden Hamilton-utat tartalmazó gráf élgráfja is tartalmaz Hamilton-utat, függetlenül attól, hogy Euler-kört is tartalmazott-e az eredeti gráf.[10]
  • Ha két gráf izomorf, élgráfjaik is izomorfak. Whitney izomorfizmustétele szerint a fordítottja is igaz, egyetlen gráf kivételével.
  • A komplex hálózatok elméletében egy véletlen hálózat élgráfja megőrzi a hálózat számos tulajdonságát, köztük a kisvilág-tulajdonságot (bármely két csúcspár közötti rövid út létezése) és a fokszámeloszlás alakját[11] (Evans & Lambiotte 2009) megfigyelése szerint a komplex hálózatban csúcsklaszterek keresésére alkalmazott módszerek használhatól az élgráf élklaszterezésére is.

Whitney izomorfizmustétele[szerkesztés]

gyémántgráf(wd), kivétel az erős Whitney-tétel alól

Ha két összefüggő gráf élgráfjai izomorfak, az eredeti gráfok is izomorfak, kivéve a K3 háromszöggráf és a K1,3 csillaggráf esetét, melyek élgráfjai izomorfak, de ők maguk nem azok.[4]

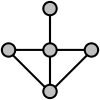
A K3 és K1,3 esetén kívül van néhány kivételes, kis méretű gráf, melyek élgráfja nagyobb szimmetriát mutat az eredeti gráfnál. Például a K1,1,2 gyémántgráf (két, közös éllel rendelkező háromszög) négy gráfautomorfizmussal rendelkezik, de élgráfja, a K1,2,2 nyolccal. A gyémántgráf illusztrációján látható, hogy a gráf 90 fokkal történő elforgatása nem szimmetriája a gráfnak, az élgráfjának azonban igen. Az ilyen kivételes esetek azonban legfeljebb négy csúcsszámú gráfoknál fordulnak elő. Whitney izomorfizmus-tételének erős változata szerint négy csúcsnál többet tartalmazó összefüggő gráfok esetében 1:1 megfeleltetés létezik a gráfok izomorfizmusai és élgráfjaik izomorfizmusai között.[12]

A Whitney-izomorfizmustételnek léteznek multigráfok élgráfjaira vonatkozó változatai, de azok komplikáltabbak.[13]

Erősen reguláris élgráfok és élperfekt gráfok[szerkesztés]

Egy élperfekt gráf. Minden kétszeresen összefüggő komponens éleit feketére színeztük, ha a komponens páros, kékre, ha a komponens tetraéder és pirosra, ha a komponens háromszögekből álló könyv.

A Kn teljes gráf élgráfja a trianguláris gráf vagy J(n,2) Johnson-gráf, ami a KGn,2 Kneser-gráf komplementere. A trianguláris gráfokat jellemzi spektrumuk, kivéve az n = 8 esetet.[14] Jellemezhetők úgy is (ismét a K8 kivételével) mint olyan erősen reguláris gráfok, melynek paraméterei srg(n(n − 1)/2, 2(n − 2), n − 2, 4).[15] A három erősen reguláris gráfot, aminek paraméterei és spektruma megegyezik az L(K8) gráffal Chang-gráfoknak nevezik, melyek az L(K8)-ból gráfkapcsolással állíthatók elő.

A páros gráf élgráfja mindig perfekt gráf (lásd Kőnig-tétel). A páros gráfok élgráfjai fontos szerepet játszanak a perfekt gráfok vizsgálatában, felhasználták az erős perfektgráf-tétel bizonyítása során is.[16] Az ilyen gráfok speciális esetei a bástyagráfok, melyek a teljes páros gráfok élgráfjai. A teljes gráfok élgráfjaihoz hasonlóan egyetlen kivétellel jellemzi őket csúcsaik, éleik, illetve a szomszédos és nem szomszédos csúcsokkal közös szomszédjaik száma. Az egyetlen kivételes eset az L(K4,4), aminek paraméterei a Shrikhande-gráffal egyeznek meg. Ha a páros gráf mindkét partíciójában ugyanannyi csúcs található, ezek az élgráfok szintén erősen regulárisak.[17]

Általánosabban, ha L(G) perfekt gráf, G gráfot élperfekt gráfnak nevezzük. Az élperfekt gráfok pontosan azok a gráfok, melyek nem tartalmaznak páratlan hosszúságú, háromnál nagyobb egyszerű kört.[18] Ezzel ekvivalens állítás, hogy egy gráf akkor és csak akkor élperfekt, ha minden kétszeresen összefüggő komponense vagy páros, vagy K4 (tetraéder) vagy egy K1,1,n teljes háromrészes gráf (közös élből kiinduló háromszögekből álló „könyv”).[19] Minden élperfekt gráf egyben perfekt gráf is.[20]

Egyéb kapcsolódó gráfcsaládok[szerkesztés]

Minden élgráf karommentes gráf, tehát olyan gráf, melynek nem feszített részgráfja a háromlevelű fa.[21] Ahogy az a karommentes gráfokra általában is igaz, bármely összefüggő, páros számú éllel rendelkező L(G) élgráf teljes párosítással rendelkezik.[22]

A fák élgráfjai karommentes blokkgráfok.[23] Ezek a gráfok szerepet játszanak az extremális gráfelmélet egy problémájának megoldásában; olyan gráf szerkesztésében, melynek csúcs- és élszáma adott, és melyben a legnagyobb feszített részfa a lehető legkisebb méretű.[24]

Egy élgráf szomszédsági mátrixának sajátértékeinek nagysága legalább −2. Emiatt az ilyen szomszédsági mátrix sajátértékkel rendelkező gráfokat egyesek általánosított élgráfoknak tekintik.[25]

Jellemzés és felismerés[szerkesztés]

Klikkpartíció[szerkesztés]

Élgráf klikkekre particionálása

Bármely G gráf egy tetszőlegesen kiválasztott v csúcsa esetében a v-ből kiinduló élek megfelelnek az L(G) élgráf egy klikkjének. Az így kialakuló klikkek particionálják L(G) éleit. Minden L(G)-beli csúcs pontosan két klikkhez tartozik (a G-beli él két végpontjának megfelelő két klikkhez).

Az említett klikkekre való particionálás létezése alkalmas az élgráfok jellemzésére: Egy L gráf akkor és csak akkor az élgráfja valamely gráfnak vagy multigráfnak, ha lehetséges L-ben klikkek olyan gyűjteményét azonosítani (megengedve, hogy egyes klikkek egyetlen csúcsból álljanak), melyek L éleit úgy particionálják, hogy L minden csúcsa pontosan két klikkbe tartozzon.[21] Gráf (és nem multigráf) élgráfjáról van szó, ha a klikkek halmaza teljesíti még azt a feltételt is, hogy L semelyik két csúcsa nem tartozik ugyanabba a két klikkbe. Egy ilyen klikkcsalád segítségével úgy nyerhető vissza L-ből az eredeti G gráf, hogy minden klikkhez egy csúcsot hozunk létre G-ben, majd minden L-beli csúcshoz egy olyan élet, melynek végpontjai a csúcsot tartalmazó két L-beli klikk. A Whitney-féle izomorfizmustétel erős változata alapján, ha G-nek négynél több csúcsa van, csak egyetlen ilyen partíció létezhet.

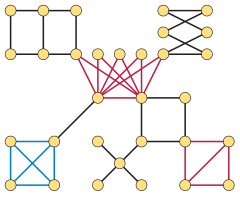
Tekintsük az alábbi gráfot, mely a fenti jellemzők alapján nem egy élgráf:

A példabeli gráf középső, negyedfokú csúcsából felfelé, balra és jobbra induló élek nem osztoznak közös klikken. Ezért bármely, a gráf éleit klikkekbe osztó particionálás legalább egy klikket rendelne ehhez a három élhez, melyek mind a középső csúcsban metszenék egymást, megsértve a követelményt, hogy minden csúcsnak pontosan két klikkbe kell tartoznia. Tehát a fenti gráf nem élgráf.

Tiltott részgráfok[szerkesztés]

A kilenc minimális nem-élgráf, az élgráfok Beineke-féle tiltottrészgráf-karakterizációjából. Egy gráf akkor és csak akkor élgráf, ha egyet sem tartalmaz feszített részgráfként az ábrán látható gráfokból.

Az élgráfok egy alternatív karakterizációját (Beineke 1970) végezte el (korábban bizonyítás nélkül: (Beineke 1968)). Megmutatta, hogy létezik kilenc olyan minimális gráf, melyek nem élgráfok, és ha egy gráf tartalmazza bármelyiket feszített részgráfként, akkor az a gráf sem lehet élgráf. Tehát egy gráf akkor és csak akkor élgráf, ha csúcsainak semelyik részhalmaza nem tartalmazza az említett kilenc gráfot. A fenti példában a négy felső csúcs tartalmazza a karmot (tehát a K1,3 teljes páros gráfot), amely a tiltott gráfok illusztrációi közül a bal felső az ábrán. Tehát Beineke jellemzése szerint sem lehet a példa élgráf. Az olyan gráfok esetében, ahol a csúcsok minimális fokszáma 5, csak a bal és jobb oszlop részgráfjait kell vizsgálni a karakterizáció során.[26] A multigráfok élgráfjait hasonlóan jellemzi Beineke kilenc tiltott részgráfja közül három.[27]

Algoritmusok[szerkesztés]

(Roussopoulos 1973) és (Lehot 1974) lineáris idejű algoritmusokat írnak le az élgráfok felismerésére és az eredeti gráfok rekonstrukciójára. (Sysło 1982) általánosította ezeket a módszereket irányított gráfokra. (Degiorgi & Simon 1995) hatékony adatstruktúrát írt le egy dinamikus gráf karbantartására, melyhez csúcsokat lehet hozzáadni és csúcsokat törölni, miközben a bemeneti gráf élgráfjának (ha az létezik) reprezentációját az egyes lépésekben megváltozott élekkel egyenes arányban lévő időben karban tartja.

A (Roussopoulos 1973) és (Lehot 1974) által használt algoritmusok az élgráfok páratlan háromszögeken alapuló karakterizációján alapulnak (az élgráfban lévő háromszögek, melyek azzal a tulajdonsággal rendelkeznek, hogy létezik másik csúcs páratlan számú háromszögben lévő csúcsokkal). (Degiorgi & Simon 1995) algoritmusa azonban kizárólag Whitney izomorfizmustételét használja. Elbonyolítja az algoritmust, hogy fel kell ismernie az olyan törléseket, amiktől megmaradó gráf élgráf lesz, de ha a statikus felismerésre specializálják, akkor kizárólag csúcshozzáadásokat kell elvégezni, és ekkor az algoritmus a következő lépésekből áll:

  • Alkossuk meg a bemeneti L gráfot csúcsok egyenkénti hozzáadásával oly módon, hogy minden lépésben olyan csúcsot válasszunk, ami szomszédos egy korábban hozzáadott csúccsal. Miközben csúcsokat adunk L-hez, tartsuk meg a G gráfot, melyre L = L(G); ha az algoritmusnak nem sikerül egy lépésben a megfelelő G gráf megtalálása, akkor a bemenet nem élgráf és az algoritmus megáll.
  • Amikor hozzáadunk egy v csúcsot egy az L(G) gráfhoz, és G-nek éppen négy vagy kevesebb csúcsa van, előállhat az eset, amikor az élgráf-reprezentáció nem egyedi. Ekkor azonban a gráf még elég kicsi ahhoz, hogy egy brute force-kereséssel meg lehessen találni konstans időben a megfelelő megoldást.
  • Amikor egy G gráf nagyobb L élgráfjához hozzáadunk egy v csúcsot, legyen S G azon részgráfja, amik megfelelnek v L-beli szomszédainak. Ellenőrizzük, hogy S-nek létezik csúcslefedése, ami egy csúcsból vagy két nem szomszédos csúcsból áll. Ha a lefedés két csúcsból áll, bővítsük G-t egy v-nek megfelelő él hozzáadásával, ami összeköti a két csúcsot. Ha csak egy csúcsból áll a lefedés, adjuk új csúcsot G-hez, ezen csúccsal szomszédosan.

Az algoritmus minden lépése vagy konstans időt vesz igénybe, vagy magában foglalja egy konstans méretű csúcslefedés megkeresését az S gráfon belül, mely utóbbinak mérete arányos v szomszédainak számával. Így tehát az algoritmus teljes futási ideje arányos az összes csúcs szomszédainak számával, ami a kézfogás-lemma alapján arányos a bemeneti élek számával.

Az élgráf-művelet iterációja[szerkesztés]

(van Rooij & Wilf 1965) vizsgálják a következő gráfsorozatot:

Megmutatják, hogy ha G véges összefüggő gráf, négy lehetséges kimenetele van ennek a sorozatnak:

  • Ha G körgráf, akkor L(G) és a sorozat további tagjai izomorfak G-vel. Ez az egyetlen eset összefüggő gráfok esetében, ahol L(G) izomorf G-vel.[28]
  • Ha G éppen a K1,3 csillaggráf (karom), akkor L(G) és az összes többi eleme a sorozatnak háromszöggráf (azaz a körgráf).
  • Ha G útgráf, akkor minden rákövetkező gráf a sorozatban eggyel rövidebb útgráf egészen addig, míg a sorozat üres gráfban végződik.
  • Minden más esetben a gráfok mérete korlát nélkül növekszik.

Ha G nem összefüggő gráf, akkor a fenti osztályozást G komponensein külön-külön kell elvégezni.

Az olyan összefüggő gráfokra alkalmazva az élgráf-műveletet, melyek nem útgráfok, akkor elegendően nagy számú iteráció után Hamilton-gráfot kapunk.[29]

Általánosítások[szerkesztés]

Mediális gráfok és konvex poliéderek[szerkesztés]

Bővebben: Mediális gráf

Ha egy G síkgráf maximális fokszáma három, akkor élgráfja síkba rajzolható és G minden síkba illesztése kiterjeszthető L(G) egy síkba illesztésére. A magasabb fokú síkgráfok közül azonban léteznek olyan, melyek élgráfjai nem síkgráfok. Ezek közé tartozik például a K1,5 csillaggráf, az ékkőgráf ( legyezőgráf), mely egy szabályos ötszög két nem metsző átlójának berajzolásával kapható meg, valamint az összes konvex poliéder, melynek maximális fokszáma 4 vagy több.[30]

Egy alternatív konstrukció, a mediális gráf legfeljebb három fokszámú síkgráfok esetében egybeesik az élgráffal. Ugyanannyi csúcsa van, mint az élgráfnak, de potenciálisan kevesebb éle: a mediális gráf csúcsai akkor és csak akkor vannak éllel összekötve, ha a két él a síkbarajzolt gráf ugyanazon tartományában egymás után következik. Egy síkgráf duális gráfjának mediális gráfja megegyezik az eredeti gráf mediális gráfjával.[31]

Szabályos vagy egyszerű testek mediális gráfjának létrehozása mértanilag úgy is kifejezhető, hogy a test minden csúcsát levágjuk egy olyan síkkal, ami a szomszédos élek középpontjain halad keresztül.[32] Ezt a műveletet angol nyelvterületen úgy is ismerik, mint second truncation,[33] degenerate truncation[34] vagy rectification.[35]

Totális gráfok[szerkesztés]

Egy G gráfhoz tartozó T(G) totális gráf csúcsként tartalmazza G összes elemét (csúcsát és élét), csúcsai között pedig akkor van él, ha az eredeti gráfban az elemek között bármilyen (él–él, csúcs–csúcs vagy csúcs–él) szomszédsági viszony volt. A totális gráf megkapható úgy is, ha G minden élét felbontjuk, majd a felbontott gráfot második hatványra emeljük.[36]

Multigráfok[szerkesztés]

G gráf élgráfjának koncepcióját viszonylag természetes módon ki lehet terjeszteni arra az esetekre, amikor G multigráf. Ebben az esetben az élgráfok karakterizációja egyszerűsödik: a klikkekre particionáláskor nem tilos, hogy két csúcs ugyanabba a két klikkbe tartozzon, és a tiltott gráf-alapú karakterizáció során is kevesebb tiltott gráfra van szükség.[27]

Ami viszont lényeges változás, hogy multigráfok esetében több olyan nem izomorf gráf-páros létezik, melyeknek ugyanaz az élgráfja. Például a K1,n teljes páros gráfnak ugyanaz az élgráfja, mint az ugyanannyi éllel rendelkező dipólusgráfnak és a Shannon-multigráfnak. Mindenesetre a Whitney-féle izomorfizmustétel analóg változata a multigráfok élgráfjaira is megfogalmazható.[13]

Irányított élgráfok[szerkesztés]

De Bruijn-gráfok konstrukciója iterált irányított élgráfként

Lehetséges az élgráfok általánosítása irányított gráfokra is.[37] Ha G irányított gráf, irányított élgráfjának egy csúcsa van minden egyes G-beli élhez. Az élgráf két csúcsa között, melyek a G gráfban u-ból v-be és a w-ből x-be mutató irányított éleket jelképezik, akkor létezik az uv és wx közti él, ha v = w. Tehát G élgráfjának mindegyik éle egy kettő hosszúságú irányított utat reprezentál G-ben. A De Bruijn-gráfok létrehozhatók ennek az irányított élgráf-készítési folyamatnak az ismétlésével, egy teljes irányított gráfból kiindulva.[38]

Súlyozott élgráfok[szerkesztés]

Egy L(G) élgráfban, a G gráfban lévő minden k fokszámú csúcs k(k-1)/2 élet hoz létre. A vizsgálatok számos fajtájában ez azt jelenti, hogy G magas fokszámú csúcsai túl vannak reprezentálva L(G)-ben. Tekintsünk egy G csúcsain történő véletlen sétát. Ez valamely e élen f gyakorisággal fog áthaladni. Másrészről azonban, feleljen meg ez az e él az L(G) élgráf egy v csúcsának. Ha az élgráf csúcsai között végezzük el a véletlen sétát, a v látogatási gyakorisága teljesen eltérhet f-től. Ha a G-ben lévő e élünk O(k) fokszámú csúcsokhoz kapcsolódott, O(k2)-szer gyakrabban fog bejáródni az L(G) élgráfban. Másként fogalmazva, a Whitney-féle gráfizomorfizmus-tétel garantálja, hogy az élgráf szinte mindig pontosan kódolja az eredeti gráf topológiáját, de nem mond semmit arról, hogy a két gráf dinamikailag hasonlóan viselkedik-e. Egy megoldás lehet súlyozott élgráf létrehozása, tehát egy súlyozott élekkel rendelkező gráfról van szó. Ezt több természetesnek látszó módon is el lehet végezni.[39] Például ha a G gráfban a d és e élek egy k fokszámú v csúcsban érnek össze, akkor az L(G) élgráfban a d és e csúcsokat összekötő élnek 1/(k-1) súlyt adhatunk. Ilyen módon G minden éle (feltéve hogy egyik él sem csatlakozik '1' fokszámú csúcshoz) 2 erősségű lesz az L(G) élgráfban az él G-ben lévő két csúcspontjának megfelelően. Ez a definíció kiterjeszthető arra az esetre, ha az eredeti G gráf irányított, vagy akár maga is súlyozott volt.[40] Az alapelv minden esetben az, hogy az L(G) élgráf ne csak az eredeti gráf topológiáját, hanem a dinamikáját is tükrözze.

Hipergráfok élgráfjai[szerkesztés]

Bővebben: Hipergráf élgráfja

Egy hipergráf élei tetszőleges halmazcsaládot alkothatnak, ezért a hipergráf élgráfja ugyanaz, mint ezeknek a halmazoknak a metszési gráfja.[26]

Jegyzetek[szerkesztés]

  1. ↑ Hemminger,Beineke (1978),p.273
  2. ↑ Hemminger,Beineke (1978), p.273
  3. ↑ a b c (Harary 1972), p. 71.
  4. ↑ a b (Whitney 1932); (Krausz 1943); (Harary 1972), Theorem 8.3, p. 72. Harary megadja a tétel egyszerűsített bizonyítását itt: (Jung 1966).
  5. ↑ a b Paschos, Vangelis Th. (2010), Combinatorial Optimization and Theoretical Computer Science: Interfaces and Perspectives, John Wiley & Sons, p. 394, ISBN 9780470393673, <http://books.google.com/books?id=bOMH9fPOicgC&pg=PA394>
  6. ↑ Az izolált csúcsok vizsgálatának szükségességét (Cvetković, Rowlinson & Simić 2004) mondja ki, p. 32.
  7. ↑ (Harary 1972), Theorem 8.1, p. 72.
  8. ↑ Diestel, Reinhard (2006), Graph Theory, vol. 173, Graduate Texts in Mathematics, Springer, p. 112, ISBN 9783540261834, <http://books.google.com/books?id=aR2TMYQr2CMC&pg=PA112>. Also in free online edition, Chapter 5 ("Colouring"), p. 118.
  9. ↑ Lauri, Josef & Scapellato, Raffaele (2003), Topics in graph automorphisms and reconstruction, vol. 54, London Mathematical Society Student Texts, Cambridge: Cambridge University Press, p. 44, ISBN 0-521-82151-7, <http://books.google.com/books?id=hsymFm0E0uIC&pg=PA44>. Lauri és Scapellato szerint ez az eredmény Mark Watkins érdeme.
  10. ↑ (Harary 1972), Theorem 8.8, p. 80.
  11. ↑ Ramezanpour,Karimipour,Mashagh (2003)
  12. ↑ (Jung 1966); (Degiorgi & Simon 1995).
  13. ↑ a b (Zverovich 1997)
  14. ↑ van Dam, Edwin R. & Haemers, Willem H. (2003), "Which graphs are determined by their spectrum?", Linear Algebra and its Applications 373: 241–272, DOI 10.1016/S0024-3795(03)00483-X. Lásd különösen itt: Proposition 8, p. 262.
  15. ↑ (Harary 1972), Theorem 8.6, p. 79. Harary credits this result to independent papers by L. C. Chang (1959) and A. J. Hoffman (1960).
  16. ↑ Chudnovsky, Maria; Robertson, Neil & Seymour, Paul et al. (2006), "The strong perfect graph theorem", Annals of Mathematics 164 (1): 51–229, doi:10.4007/annals.2006.164.51, <http://annals.princeton.edu/annals/2006/164-1/p02.xhtml>. See also Roussel, F.; Rusu, I. & Thuillier, H. (2009), "The strong perfect graph conjecture: 40 years of attempts, and its resolution", Discrete Mathematics 309 (20): 6092–6113, DOI 10.1016/j.disc.2009.05.024.
  17. ↑ (Harary 1972), Theorem 8.7, p. 79. Harary a teljes páros gráfok élgráfjainak jellemzését Moon and Hoffman-nak tulajdonítja. A két partícióban azonos számú csúcsok esetét korábban Shrikhande igazolta.
  18. ↑ (Trotter 1977); (de Werra 1978).
  19. ↑ Maffray,1992
  20. ↑ Trotter,1977
  21. ↑ a b (Harary 1972), Theorem 8.4, p. 74, három ekvivalens jellemzést ad az élgráfokra: az élek klikkekbe való particionálását, a karommentességet és páratlan gyémántgráf-mentességet, valamint Beineke kilenc tiltott részgráfját.
  22. ↑ Sumner, David P. (1974), "Graphs with 1-factors", Proceedings of the American Mathematical Society (American Mathematical Society) 42 (1): 8–12, DOI 10.2307/2039666. Las Vergnas, M. (1975), "A note on matchings in graphs", Cahiers du Centre d'Études de Recherche Opérationnelle 17 (2-3-4): 257–260.
  23. ↑ (Harary 1972), Theorem 8.5, p. 78. Harary credits the result to Gary Chartrand.
  24. ↑ Erdős, Paul; Saks, Michael & Sós, Vera T. (1986), "Maximum induced trees in graphs", Journal of Combinatorial Theory, Series B 41 (1): 61–79, DOI 10.1016/0095-8956(86)90028-6.
  25. ↑ Cvetković,Rowlinson,Simić (2004)
  26. ↑ a b (Metelsky & Tyshkevich 1997)
  27. ↑ a b (Harary 1972), Exercise 8.14, p. 83.
  28. ↑ Az eredmény szintén (Harary 1972) Theorem 8.2-jében található.
  29. ↑ (Harary 1972), Theorem 8.11, p. 81. Harary az eredményt Gary Chartrand-nak tulajdonítja.
  30. ↑ (Sedláček 1964); (Greenwell & Hemminger 1972).
  31. ↑ Archdeacon, Dan (1992), "The medial graph and voltage-current duality", Discrete Mathematics 104 (2): 111–141, DOI 10.1016/0012-365X(92)90328-D.
  32. ↑ McKee, T. A. (1989), "Graph-theoretic model of geographic duality", Combinatorial Mathematics: Proceedings of the Third International Conference (New York, 1985), vol. 555, Ann. New York Acad. Sci., New York: New York Acad. Sci., pp. 310–315, DOI 10.1111/j.1749-6632.1989.tb22465.x.
  33. ↑ Pugh, Anthony (1976), Polyhedra: A Visual Approach, University of California Press, ISBN 9780520030565.
  34. ↑ Loeb, Arthur Lee (1991), Space Structures—their Harmony and Counterpoint (5th ed.), Birkhäuser, ISBN 9783764335885.
  35. ↑ Weisstein, Eric W.: Rectification (angol nyelven). Wolfram MathWorld
  36. ↑ (Harary 1972), p. 82.
  37. ↑ Harary,Norman (1960)
  38. ↑ Zhang,Lin (1987)
  39. ↑ Evans,Lambiotte (2009)
  40. ↑ Evans,Lambiotte (2010)

Irodalom[szerkesztés]

További információk[szerkesztés]

A lap eredeti címe: „https://hu.wikipedia.org/w/index.php?title=Élgráf&oldid=25467815”