Petersen-gráf

Petersen-gráf
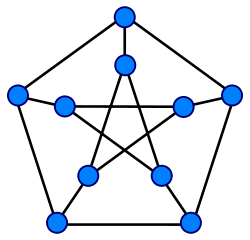A Petersen-gráf tipikus rajzolási módja
Névadó	Julius Petersen
Csúcsok száma	10
Élek száma	15
Sugár	2
Átmérő	2
Kromatikus szám	3
Élkromatikus szám	4
Egyéb	3-reguláris

A Petersen-gráf egy nagyon híres, speciális gráf. Nagyon gyakran bukkan fel a gráfelméletben különféle állítások ellenpéldájaként. 10 csúcsa és 15 éle van. Bár a névadó Julius Petersen, aki 1898-ban konstruálta meg, ezt a gráfot már 12 évvel Petersen munkája előtt 1886-ban felfedezték.

A gráf konstrukciója

Legyen $P=\left\{\ 0,1,2,3,4\right\}\$ egy 5 elemű halmaz. Ebből a $P\$ halmazból kiválasztjuk az összes kételemű részhalmazt. Ezek száma: ${{5}\choose{2}}=10$. Ezeket a kételemű halmazokat megfeleltetjük a gráf csúcsainak: $V = \{ \{0,1\}, \{0, 2\}, \{0, 3\}, \{0, 4\}, \{1, 2 \}, \{1, 3 \}, \{1, 4 \}, \{2, 3 \}, \{2, 4 \}, \{3, 4 \} \}$

Akkor van él a gráfban két $u, v \in V$ csúcs között, ha a csúcsoknak megfelelő halmazok diszjunktak.

$E = \{ \{u, v\} \in {{V}\choose{2}} : u \cap v = \emptyset \}$

Ez a konstrukció természetesen nem csak 5, hanem más számosságok esetén is működik. Átalános esetben az ilymódon konstruált gráfokat Kneser-gráfoknak nevezzük, tehát a Petersen-gráf egy speciális Kneser-gráf: $KG(5,2)\$.

Ez a gráf is izomorf a Petersen-gráffal.

• 

  A Petersen gráf keresztezési száma 2.

• 

  A Petersen gráf lerajzolható a síkban úgy, hogy minden él hossza egység hosszúságú.

• 

  A Petersen gráf egy másik rajzolási módja. Ez hármas szimmmetriát mutat, szemben a fenti rajzzal, amely ötös szimmetriával rendelkezik.

Petersen motivációja

A négyszín-sejtés egy ekvivalens alakja, hogy tetszőleges kétszeresen élösszefüggő, 3-reguláris síkgráf élhalmaza három teljes párosításra bontható. Petersen a fenti példával megmutatta, hogy a síkbarajzolhatóság feltétele nem hagyható el. Bebizonyította viszont azt a gyengébb állítást, hogy minden kétszeresen élösszefüggő, 3-reguláris síkgráfban van teljes párosítás.

Hamilton-út és Hamilton-kör

A Petersen-gráf csúcstranzitív, van benne Hamilton-út, de nincs Hamilton-kör.

Színezhetőség

A Petersen gráf kromatikus száma 3

A Petersen gráf 3 színnel színezhető, tehát kromatikus száma 3.