Komplementer gráf

A matematika, azon belül a gráfelmélet területén egy G gráf komplementere (complement) alatt azt a H gráfot értjük, melynek csúcsai megegyeznek G csúcsaival, és két csúcs pontosan akkor szomszédos H-ban, ha azok nem szomszédosak G-ben. Vizuálisan, egy gráf komplementerének előállításához be kell húzni a teljes gráfhoz szükséges éleket, majd kitörölni az addig jelen lévőket.[1] A gráf komplementere nem egyezik meg a gráf halmazelméleti komplementerével, hiszen csak az élhalmaz komplementerét képezzük.
Definíció[szerkesztés]
Legyen G = (V, E) egyszerű gráf és K álljon V összes kételemű részhalmazából. Ekkor H = (V, K \ E) megegyezik G komplementerével,[2] ahol K \ E az E halmaz K-ra vonatkozó (halmazelméleti) komplementere. Irányított gráfokban a komplementert hasonlóan definiálhatjuk, csak az előző képletben kételemű részhalmazok helyett a kételemű rendezett párokat kell venni. Multigráf komplementere nem definiált. Az olyan gráfokban, melyekben a hurok megengedett (de többszörös élek nem), G komplementere esetleg definiálható az előzőekhez képest azzal a kiegészítéssel, hogy a hurkot nem tartalmazó csúcsokhoz a komplementer gráfban hurkot adunk és megfordítva; ez azonban már jelentősen különbözne az egyszerű gráfokon értelmezett komplementerképzés műveletétől.
Alkalmazások és példák[szerkesztés]
A komplementerképzés művelete több gráfelméleti fogalmat párba állít:
- Az élmentes gráf komplementere a teljes gráf, és viszont.
- A G gráf komplementerének bármely feszített részgráfja megegyezik a G-ben neki megfelelő feszített részgráf komplementerével.
- Egy gráf bármely független csúcshalmaza a komplementer gráfban klikket alkot és vice versa. Ez voltaképpen az előző két fogalompár speciális esete, hiszen egy független csúcshalmaz egy élmentes feszített részgráf, a klikk pedig egy teljes feszített részgráf.
- Egy gráf automorfizmuscsoportja a komplementer gráf automorfizmuscsoportja is.
- Minden háromszögmentes gráf komplementere karommentes gráf,[3] bár az állítás fordítottja nem igaz.
Önkomplementer gráfok és gráfosztályok[szerkesztés]
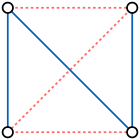
Egy önkomplementer gráf olyan gráf, ami izomorf saját komplementerével.[1] Példa erre a négy csúcs hosszúságú útgráf és az öt hosszúságú körgráf. Számos gráfcsalád tekinthető önkomplementernek, abban az értelemben, hogy a családba tartozó bármely gráf komplementere is a családba tartozik.
- Egy perfekt gráf olyan a gráf, melynek minden feszített részgráfjának kromatikus száma megegyezik a maximális klikkjének méretével. Lovász László perfektgráf-tétele értelmében minden perfekt gráf komplementere is perfekt.[4]
- A kográfok azok a gráfok, melyek egyetlen csúcsból kiindulva előállíthatók a komplementerképzés és a diszjunkt unió gráfműveletek segítségével. Önkomplementer gráfcsaládot alkotnak, bármely kográf komplementere egy másik kográf. Mivel az egynél több csúcsú kográfok esetében egy komplementer-kográfpárosból mindig csak egy gráf összefüggő, ezért a kográfok egy ekvivalens definíciója szerint minden összefüggő feszített részgráfjuk komplementere nem összefüggő. Egy másik, önkomplementer definíció szerint a kográfok azok a gráfok, melyek nem tartalmazzak a négy csúcsból álló utat feszített részgráfként.[5]
- Egy másik önkomplementer család a split gráfoké; ezek a gráfok, melyek csúcsai egy klikkbe és egy független csúcshalmazba particionálhatók. Ugyanez a partíció a komplementer gráfban is egy független halmazt, illetve klikket ad.[6]
- A küszöbgráfok azok a gráfok, melyek egyetlen csúcsból kiindulva előállíthatók egy független (szomszédok nélküli) csúcs, illetve egy univerzális csúcs (minden korábbi csúccsal szomszédos csúcs) hozzáadásának műveleteivel. Ez a két művelet komplementer jellegű, és együtt gráfok önkomplementer családját állítják elő.[7]
Algoritmikus aspektusok[szerkesztés]
A gráfalgoritmusok analízise során a gráf és komplementere közötti különbségtétel általában lényeges, hiszen egy ritka gráf (a csúcsaihoz képest kevés éllel rendelkező gráf) komplementere általában nem ritka, ezért egy a gráf éleinek számával arányos algoritmus a ritka gráf komplementerének valamely explicit reprezentációján sokkal hosszabb ideig futhat. Ezért a kutatók olyan algoritmusokat is vizsgálnak, melyek a gráfokkal kapcsolatos számításokat a bemeneti gráf komplementerén végzik, egy olyan implicit gráfreprezentációt felhasználva, melyhez nem szükséges a komplementer gráf explicit megkonstruálása. Lehetséges például a komplementer gráfon akár mélységi, akár szélességi keresést végezni a gráf mérete szerint lineáris időben, még akkor is, ha a komplementer gráf mérete sokkal nagyobb.[8] Ezek a szimulációk használhatók a komplementer gráf összefüggőségét érintő egyéb tulajdonságok számításánál is.[8][9]
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a Complement graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek[szerkesztés]
- ↑ a b Bondy, John Adrian & Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, p. 6, ISBN 0-444-19451-7, <http://www.maths.lse.ac.uk/Personal/jozef/LTCC/Graph_Theory_Bondy_Murty.pdf>.
- ↑ Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6. Electronic edition, page 4.
- ↑ Chudnovsky, Maria & Seymour, Paul (2005), "The structure of claw-free graphs", Surveys in combinatorics 2005, vol. 327, London Math. Soc. Lecture Note Ser., Cambridge: Cambridge Univ. Press, pp. 153–171.
- ↑ Lovász, László (1972a), "Normal hypergraphs and the perfect graph conjecture", Discrete Mathematics 2 (3): 253–267, DOI 10.1016/0012-365X(72)90006-4.
- ↑ Corneil, D. G.; Lerchs, H. & Stewart Burlingham, L. (1981), "Complement reducible graphs", Discrete Applied Mathematics 3 (3): 163–174, DOI 10.1016/0166-218X(81)90013-5.
- ↑ Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, Theorem 6.1, p. 150, ISBN 0-12-289260-7.
- ↑ Golumbic, Martin Charles & Jamison, Robert E. (2006), "Rank-tolerance graph classes", Journal of Graph Theory 52 (4): 317–340, DOI 10.1002/jgt.20163.
- ↑ a b Ito, Hiro & Yokoyama, Mitsuo (1998), "Linear time algorithms for graph search and connectivity determination on complement graphs", Information Processing Letters 66 (4): 209–213, DOI 10.1016/S0020-0190(98)00071-4.
- ↑ Kao, Ming-Yang; Occhiogrosso, Neill & Teng, Shang-Hua (1999), "Simple and efficient graph compression schemes for dense and complement graphs", Journal of Combinatorial Optimization 2 (4): 351–359, DOI 10.1023/A:1009720402326.
