Klikkszélesség

Egy 3 klikkszélességű távolság-örökletes gráf konstrukciója diszjunkt uniókkal, átcímkézésekkel és címke-egyesítésekkel. A címkéket az ábrán színek jelzik.

A matematika, azon belül a gráfelmélet területén egy gráf klikkszélessége (clique-width) a gráf szerkezetének bonyolultságát leíró paraméter; közeli rokona a faszélességnek, de attól eltérő módon, sűrű gráfokon is korlátos lehet az értéke. A definíció szerint értéke megegyezik a $G$ gráf konstruálásához szükséges címkék minimális számával, ha a következő négy művelet engedélyezett:

1. Felveszünk egy új csúcsot, v-t és i címkével látjuk el (jelölés: i(v) vagy $\bullet _{i}$)
2. Két címkézett gráf, G és H diszjunkt unióját képezzük (jelölés: $G\oplus H$)
3. Minden i-vel jelölt csúcsot összekötünk minden j-vel jelölt csúccsal (jelölés: η(i,j)), ahol $i\neq j$
4. Átnevezzük az i címkét j-re (jelölés: ρ(i,j) )

A korlátos klikkszélességű gráfok közé tartoznak a kográfok és a távolság-örökletes gráfok is. Bár általános esetben a klikkszélesség meghatározása NP-nehéz feladat, és nem tudjuk, vajon polinom időben kiszámítható-e abban az esetben, ha korlátos, ismert több hatékony közelítő algoritmus a klikkszélesség kiszámítására. Ezekre az algoritmusokra és a Courcelle-tételre alapozva számos, általános gráfokon NP-nehéz gráfoptimalizálási probléma gyorsan megoldható vagy közelíthető a korlátos klikkszélességű gráfokon.

A klikkszélesség fogalmához szükséges konstrukciós lépéseket Courcelle, Engelfriet és Rozenberg fogalmazta meg 1990-ben , majd (Wanke 1994). A „klikkszélesség” kifejezést először (Chlebíková 1992) használta egy másik fogalom leírására, de 1993-ra már a jelenlegi értelemben használták.

Példa

A $C_{6}$ konstrukciós lépéseinek kifejezés-fája

A 6 csúcsból álló $C_{6}$ gráf klikkszélessége nem nagyobb 3-nál, mivel a következő műveletek segítségével előállítható:

Klikkszélesség-művelet	A gráf vizualizációja
$G_{1}=\bullet _{1}$
$G_{2}=\bullet _{2}$
$G_{3}=G_{1}\oplus G_{2}$
$G_{4}=\eta _{1,2}(G_{3})$
$G_{5}=G_{4}\oplus G_{4}$
$G_{6}=G_{5}\oplus \bullet _{3}$
$G_{7}=\eta _{1,3}(G_{6})$
$G_{8}=\rho _{3\rightarrow 1}(G_{7})$
$G_{9}=G_{8}\oplus \bullet _{3}$
$C_{6}=\eta _{2,3}(G_{9})$

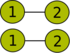
Az előállított $3$-művelet a következő:

$X=\eta _{2,3}(\rho _{3\rightarrow 1}(\eta _{1,3}(\eta (\bullet _{1}\oplus \bullet _{2})\oplus \eta (\bullet _{1}\oplus \bullet _{2})\oplus \bullet _{3}))\oplus \bullet _{3})$

A jobb oldalon látható az $X$ 3-kifejezés fája.

Speciális gráfosztályok

A kográfok megegyeznek azokkal a gráfokkal, melyek klikkszélessége legfeljebb 2. A távolság-örökletes gráfok klikkszélessége legfeljebb 3. Az egység-intervallumgráfok klikkszélessége azonban (rácsos szerkezetük miatt) korlátlan. Hasonlóan, a páros permutációgráfok klikkszélessége (hasonlóan a rácsos szerkezet maitt) korlátlan. A kográfok egyik karakterizálása szerint ezek a gráfok, melyeknek nincs négy csúcsból álló húrmentes úttal izomorf feszített részgráfja. Ebből kiindulva számos, tiltott feszített részgráfok alapján meghatározott gráfcsalád klikkszélességét sikerült megállapítani.

A korlátos klikkszélességű gráfok közé tartoznak még a k-adik levélhatványok is a k korlátos értékeire; ezek a T^k gráfhatvány T levelei által kifeszített részgráfjai. A nem korlátos kitevőjű levélhatványok esetében azonban a klikkszélesség sem korlátos.

Korlátok

(Courcelle & Olariu 2000) és (Corneil & Rotics 2005) egyes gráfok klikkszélességével kapcsolatban a következőket igazolták:

• Ha egy gráf klikkszélessége legfeljebb k, akkor ez igaz a gráf minden feszített részgráfjára is.
• Egy k klikkszélességű gráf komplementerének klikkszélessége legfeljebb 2k.
• A w faszélességű gráfok klikkszélessége legfeljebb 3 · 2^{w − 1}. A korlátban szereplő exponenciális tag szükséges: ténylegesen léteznek olyan gráfok, melyek klikkszélessége exponenciálisan nagyobb a faszélességüknél. Megfordítva, a korlátos klikkszélességű gráfok rendelkezhetnek korlátlan faszélességgel; például az n csúcsú teljes gráfok klikkszélessége 2, míg faszélességük n − 1. Azoknak a k klikkszélességű gráfoknak viszont, melyek nem tartalmazzák a K_t,t teljes páros gráfot részgráfként, legfeljebb 3k(t − 1) − 1 lehet a faszélességük. Így aztán, tetszőleges ritka gráfcsaládra igaz, hogy a korlátos faszélesség ekvivalens a korlátos klikkszélességgel.
• Egy további gráfparamétert, a rangszélességet (rank-width) mindkét irányból korlátok közé szorít a klikkszélesség: rangszélesség ≤ klikkszélesség ≤ 2^{rangszélesség + 1}.

Igaz továbbá, hogy ha a G gráf klikkszélessége k, akkor a G^c gráfhatvány klikkszélessége legfeljebb 2kc^k. Bár mind a klikkszélesség a faszélesség szerinti korlátjában, mind klikkszélesség gráfhatvány szerinti korlátjában exponenciális rés szerepel, ezeknek a korlátok nem szorzódnak össze: ha a G gráf faszélessége w, akkor G^c klikkszélessége legfeljebb 2(c + 1)^{w + 1} − 2, ami a faszélességnek csak egyszeresen exponenciális függvénye.

Számítási bonyolultság

A matematika megoldatlan problémája: Felismerhetők-e polinom időben a korlátos klikkszélességű gráfok? (A matematika további megoldatlan problémái)

Számos, általánosabb gráfosztályokon NP-nehéz optimalizálási probléma korlátos klikkszélességű gráfokon dinamikus programozás segítségével hatékonyan megoldható, ha ezen gráfok konstrukciós lépései ismertek. Közelebbről, minden gráftulajdonság, aminek létezése kifejezhető a gráftulajdonságokat logikai műveletekkel, kvantorokkal stb. leíró MSO₁ monadikus másodrendű logika segítségével, a Courcelle-tétel egy változata alapján lineáris idejű algoritmussal eldönthető.

Polinom időben lehetséges továbbá a korlátos klikkszélességű gráfok optimális gráfszínezését és Hamilton-körét megtalálni, ha a konstrukciós lépések ismertek, de a polinom kitevője a klikkszélességgel növekszik, és a számítási bonyolultságelmélet bizonyítékai arra mutatnak, hogy ettől a függőségtél valószínűleg nem lehet eltekinteni. A korlátos klikkszélességű gráfok χ-korlátosak, vagyis kromatikus számuk legfeljebb a legnagyobb klikk méretének függvénye lehet.

A három klikkszélességű gráfok polinom időben felismerhetők, és konstrukciós lépéseik is előállíthatók egy splitfelbontás-alapú algoritmussal. A nem korlátos klikkszélességű gráfok esetén NP-nehéz a klikkszélesség pontos megállapítása, ahogy a szublineáris additív hibával történő approximációja is. Ha azonban a klikkszélesség korlátos, egy korlátos szélességű (exponenciálisan nagyobb mint a tényleges klikkszélesség) konstrukciós lépéssorozat polinom időben előállítható. Nyitott egyelőre az a kérdés, hogy a pontos klikkszélesség, vagy akár egy pontosabb approximációja kiszámítható-e rögzített paraméter mellett kezelhető időben, polinom időben kiszámítható-e minden rögzített klikkszélesség-korlát esetén, vagy akár a négy klikkszélességű gráfok felismerhetők-e a polinom időben.

Faszélességgel való kapcsolata

A korlátos klikkszélességű gráfok elmélete hasonlít a korlátos faszélességű gráfokéhoz, de azoktól eltérően sűrű gráfokkal is foglalkozik. Ha egy gráfcsalád klikkszélessége korlátos, akkor vagy a faszélessége is korlátos, vagy minden teljes páros gráf a család valamely tagjának részgráfja. A faszélesség és a klikkszélesség az élgráfokon keresztül is összekapcsolódik: egy gráfcsalád pontosan akkor korlátos faszélességű, ha élgráfjaiknak klikkszélessége korlátos.

Fordítás

• Ez a szócikk részben vagy egészben a Clique-width című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

• Brandstädt, A.; Dragan, F.F. & Le, H.-O. et al. (2005), "New graph classes of bounded clique-width", Theory of Computing Systems 38: 623–645, DOI 10.1007/s00224-004-1154-6.
• Brandstädt, A.; Engelfriet, J. & Le, H.-O. et al. (2006), "Clique-width for 4-vertex forbidden subgraphs", Theory of Computing Systems 39: 561–590, DOI 10.1007/s00224-005-1199-1.
• Brandstädt, Andreas & Hundt, Christian (2008), "Ptolemaic graphs and interval graphs are leaf powers", LATIN 2008: Theoretical informatics, vol. 4957, Lecture Notes in Comput. Sci., Springer, Berlin, pp. 479–491, DOI 10.1007/978-3-540-78773-0_42.
• Brandstädt, A. & Lozin, V.V. (2003), "On the linear structure and clique-width of bipartite permutation graphs", Ars Combinatoria 67: 273–281.
• Chlebíková, J. (1992), "On the tree-width of a graph", Acta Mathematica Universitatis Comenianae, New Series 61 (2): 225–236.
• Cogis, O. & Thierry, E. (2005), "Computing maximum stable sets for distance-hereditary graphs", Discrete Optimization 2 (2): 185–188, DOI 10.1016/j.disopt.2005.03.004.
• Corneil, Derek G.; Habib, Michel & Lanlignel, Jean-Marc et al. (2012), "Polynomial-time recognition of clique-width ≤ 3 graphs", Discrete Applied Mathematics 160 (6): 834–865, DOI 10.1016/j.dam.2011.03.020.
• Corneil, Derek G. & Rotics, Udi (2005), "On the relationship between clique-width and treewidth", SIAM Journal on Computing 34 (4): 825–847, DOI 10.1137/S0097539701385351.
• Courcelle, Bruno; Engelfriet, Joost & Rozenberg, Grzegorz (1993), "Handle-rewriting hypergraph grammars", Journal of Computer and System Sciences 46 (2): 218–270, DOI 10.1016/0022-0000(93)90004-G. Presented in preliminary form in Graph grammars and their application to computer science (Bremen, 1990), MR1431281.
• Courcelle, B. (1993), "Monadic second-order logic and hypergraph orientation", Proceedings of Eighth Annual IEEE Symposium on Logic in Computer Science (LICS '93), pp. 179–190, DOI 10.1109/LICS.1993.287589.
• Courcelle, B.; Makowsky, J. A. & Rotics, U. (2000), "Linear time solvable optimization problems on graphs on bounded clique width", Theory of Computing Systems 33 (2): 125–150, DOI 10.1007/s002249910009.
• Courcelle, B. & Olariu, S. (2000), "Upper bounds to the clique width of graphs", Discrete Applied Mathematics 101 (1–3): 77–144, DOI 10.1016/S0166-218X(99)00184-5.
• Dvořák, Zdeněk & Král', Daniel (2012), "Classes of graphs with small rank decompositions are χ-bounded", Electronic Journal of Combinatorics 33 (4): 679–683, DOI 10.1016/j.ejc.2011.12.005
• Fellows, Michael R.; Rosamond, Frances A. & Rotics, Udi et al. (2009), "Clique-width is NP-complete", SIAM Journal on Discrete Mathematics 23 (2): 909–939, DOI 10.1137/070687256.
• Fomin, Fedor V.; Golovach, Petr A. & Lokshtanov, Daniel et al. (2010), "Intractability of clique-width parameterizations", SIAM Journal on Computing 39 (5): 1941–1956, DOI 10.1137/080742270.
• Golumbic, Martin Charles & Rotics, Udi (2000), "On the clique-width of some perfect graph classes", International Journal of Foundations of Computer Science 11 (3): 423–443, DOI 10.1142/S0129054100000260.
• Gurski, Frank & Wanke, Egon (2000), "The tree-width of clique-width bounded graphs without K_n,n", in Brandes, Ulrik & Wagner, Dorothea, Graph-Theoretic Concepts in Computer Science: 26th International Workshop, WG 2000, Konstanz, Germany, June 15–17, 2000, Proceedings, vol. 1928, Lecture Notes in Computer Science, Berlin: Springer, pp. 196–205, DOI 10.1007/3-540-40064-8_19.
• Gurski, Frank & Wanke, Egon (2007), "Line graphs of bounded clique-width", Discrete Mathematics 307 (22): 2734–2754, DOI 10.1016/j.disc.2007.01.020.
• Gurski, Frank & Wanke, Egon (2009), "The NLC-width and clique-width for powers of graphs of bounded tree-width", Discrete Applied Mathematics 157 (4): 583–595, DOI 10.1016/j.dam.2008.08.031.
• Hliněný, Petr & Oum, Sang-il (2008), "Finding branch-decompositions and rank-decompositions", SIAM Journal on Computing 38 (3): 1012–1032, DOI 10.1137/070685920.
• Oum, Sang-il & Seymour, Paul (2006), "Approximating clique-width and branch-width", Journal of Combinatorial Theory, Series B 96 (4): 514–528, DOI 10.1016/j.jctb.2005.10.006.
• Oum, Sang-il (2009), "Approximating rank-width and clique-width quickly", ACM Transactions on Algorithms 5 (1): Art. 10, 20, DOI 10.1007/11604686_5.
• Todinca, Ioan (2003), "Coloring powers of graphs of bounded clique-width", Graph-theoretic concepts in computer science, vol. 2880, Lecture Notes in Comput. Sci., Springer, Berlin, pp. 370–382, DOI 10.1007/978-3-540-39890-5_32.
• Wanke, Egon (1994), "k-NLC graphs and polynomial algorithms", Discrete Applied Mathematics 54 (2-3): 251–266, DOI 10.1016/0166-218X(94)90026-4.