„Palacsintagráf” változatai közötti eltérés
| [ellenőrzött változat] | [ellenőrzött változat] |
Syp (vitalap | szerkesztései) Nincs szerkesztési összefoglaló |
Syp (vitalap | szerkesztései) Nincs szerkesztési összefoglaló Címke: HTML-sortörés |
||
| 17. sor: | 17. sor: | ||
| jelölés = <math>P_n</math> |
| jelölés = <math>P_n</math> |
||
}} |
}} |
||
A [[matematika]], azon belül a [[gráfelmélet]] területén egy ''P''<sub>n</sub> '''palacsintagráf''', avagy '''''n''-palacsintagráf''' olyan egyszerű, irányítatlan, hurokmentes [[gráf]], melynek csúcshalmaza az 1,2,...,n számok [[permutáció]]inak (sorbaállításainak) halmaza. Két permutáció között akkor húzódik él, ha az egyik tranzitív módon átvihető a másikba egy kezdőszeletének megfordításával ''(prefix reversal)''. A '''[[palacsintarendezés]] |
A [[matematika]], azon belül a [[gráfelmélet]] területén egy ''P''<sub>n</sub> '''palacsintagráf''', avagy '''''n''-palacsintagráf''' olyan egyszerű, irányítatlan, hurokmentes [[gráf]], melynek csúcshalmaza az 1,2,...,n számok [[permutáció]]inak (sorbaállításainak) halmaza. Két permutáció között akkor húzódik él, ha az egyik tranzitív módon átvihető a másikba egy kezdőszeletének megfordításával ''(prefix reversal)''. |
||
A '''[[palacsintarendezés]]''' ''(pancake sorting)'' az a matematikai probléma, melynek során különböző méretű [[Palacsinta|palacsintákból]] álló oszlopot nagyság szerinti sorba rendeznek oly módon, hogy az oszlopba bárhol beszúrható egy fordítólapát, és az összes fölötte lévő palacsinta megfordítható vele. A palacsintarendezési probléma és a palacsintagráf [[átmérő (gráfelmélet)|átmérőjének]] meghatározása egymással ekvivalens.<ref name="pancake17">{{Cite journal|last=Asai|first=Shogo|last2=Kounoike|first2=Yuusuke||last3=Shinano|first3=Yuji|last4=Kaneko|first4=Keiichi|date=2006-09-01|title=Computing the Diameter of 17-Pancake Graph Using a PC Cluster.|url=https://link.springer.com/chapter/10.1007/11823285_117 |journal=Euro-Par 2006 Parallel Processing: 12th International Euro-Par Conference|doi=10.1007/11823285_117}}</ref> |
|||
Az ''n'' méretű palacsintagráf, P<sub>n</sub> rekurzívan előállítható a P<sub>n−1</sub> palacsintagráf ''n'' kópiájából oly módon, hogy az {1, 2, …, n} halmaz más-más elemét fűzzük hozzá az egyes kópiákhoz. |
Az ''n'' méretű palacsintagráf, P<sub>n</sub> rekurzívan előállítható a P<sub>n−1</sub> palacsintagráf ''n'' kópiájából oly módon, hogy az {1, 2, …, n} halmaz más-más elemét fűzzük hozzá az egyes kópiákhoz. |
||
==Tulajdonságai== |
|||
A P<sub>n</sub> palacsintagráf [[reguláris gráf|reguláris]], csúcsainak száma ''n!'', [[fokszám (gráfelmélet)|fokszáma]] ''n−1''. [[Girthparaméter]]e: |
A P<sub>n</sub> palacsintagráf [[reguláris gráf|reguláris]], csúcsainak száma ''n!'', [[fokszám (gráfelmélet)|fokszáma]] ''n−1''. [[Girthparaméter]]e: |
||
| 29. sor: | 32. sor: | ||
<math>n!\left( \frac{n-4}{6} \right)+1 \le \gamma(P_n) \le n!\left( \frac{n-3}{4} \right)-\frac{n}{2}+1 </math> |
<math>n!\left( \frac{n-4}{6} \right)+1 \le \gamma(P_n) \le n!\left( \frac{n-3}{4} \right)-\frac{n}{2}+1 </math> |
||
==Átmérője== |
|||
A [[palacsintarendezés]]i probléma és a palacsintagráf [[átmérő (gráfelmélet)|átmérőjének]] („palacsintaszám”) meghatározása egymással ekvivalens. |
|||
{| class="wikitable" |
|||
|+ Palacsintaszámok<br />{{OEIS|A058986}} |
|||
|<math>n</math> |
|||
| 1 || 2 || 3 || 4 || 5 || 6 || 7 || 8 || style="text-align:right"| 9 || 10 || 11 || 12 || 13 || 14 || 15 || 16 || 17 |
|||
|- |
|||
|<math>P_n</math> |
|||
| 0 || 1 || 3 || 4 || 5 || 7 || 8 || 9 || 10 || 11 || 13 || 14 || 15 || 16 || 17 || 18 || 19 |
|||
|} |
|||
A palacsintaszám, tehát az {{math|''n''}} palacsintát tartalmazó oszlop rendezéséhez mindig elégséges, minimális átfordítások száma <math>\frac{15}{14}n</math> és <math>\frac{18}{11}n</math> (kb. <math>1,07n</math> és <math>1,64n</math>) között van, de a pontos érték nem ismert.<ref>{{Cite book|author=Fertin, G. and Labarre, A. and Rusu, I. and Tannier, E. and Vialette, S. |title=Combinatorics of Genome Rearrangements|publisher= The MIT Press|year= 2009|isbn=9780262062824}}</ref> |
|||
1979-ben [[Bill Gates]] és [[Christos Papadimitriou]]<ref name=Gates1979>{{cite journal |url=http://www.cs.berkeley.edu/~christos/papers/Bounds%20For%20Sorting%20By%20Prefix%20Reversal.pdf |title=Bounds for Sorting by Prefix Reversal |journal=[[Discrete Mathematics (journal)|Discrete Mathematics]] |volume=27 |pages=47–57 |year=1979 |doi=10.1016/0012-365X(79)90068-2 |last=Gates |first=W. |last2=Papadimitriou |first2=C. |authorlink1 = Bill Gates |authorlink2 = Christos Papadimitriou}}</ref> <math>\frac{5}{3}n</math> felső korlátot igazolt. Ezt 30 évvel később <math>\frac{18}{11}n</math>-re javította a [[University of Texas at Dallas]] egyetem [[Hal Sudborough]] által vezetett kutatócsoportja.<ref name="Sudborough">{{cite web|title=Team Bests Young Bill Gates With Improved Answer to So-Called Pancake Problem in Mathematics|publisher=University of Texas at Dallas News Center|date=September 17, 2008|url=http://www.utdallas.edu/news/2008/09/17-002.php?WT.mc_id=NewsEmails&WT.mc_ev=EmailOpen|accessdate=November 10, 2008|quote=A team of UT Dallas computer science students and their faculty adviser have improved upon a longstanding solution to a mathematical conundrum known as the pancake problem. The previous best solution, which stood for almost 30 years, was devised by Bill Gates and one of his Harvard instructors, Christos Papadimitriou, several years before Microsoft was established.}}</ref> (Chitturi et al., 2009<ref>{{Cite journal|last=Chitturi|first=B.|last2=Fahle|first2=W.|last3=Meng|first3=Z.|last4=Morales|first4=L.|last5=Shields|first5=C. O.|last6=Sudborough|first6=I. H.|last7=Voit|first7=W.|date=2009-08-31|title=An (18/11)n upper bound for sorting by prefix reversals|url=http://www.sciencedirect.com/science/article/pii/S0304397508003575|journal=Theoretical Computer Science|series=Graphs, Games and Computation: Dedicated to Professor Burkhard Monien on the Occasion of his 65th Birthday|volume=410|issue=36|pages=3372–3390|doi=10.1016/j.tcs.2008.04.045}}</ref>). |
|||
2011-ben Laurent Bulteau, Guillaume Fertin és Irena Rusu<ref>{{Cite journal|journal=Journal of Computer and System Sciences|doi=10.1016/j.jcss.2015.02.003|title=Pancake Flipping Is Hard|last1=Bulteau|first1=Laurent|last2=Fertin|first2=Guillaume|last3=Rusu|first3=Irena|volume=81|number=8|pages=1556–1574|arxiv=1111.0434v1}}</ref> bebizonyították, hogy egy adott palacsintaoszlop rendezéséhez szükséges legrövidebb átfordítás-sorozat megtalálása [[NP-nehéz]] feladat. |
|||
==Égetett palacsintagráf== |
|||
Az '''égetett palacsinta-problémaként''' ''(burnt pancake problem)'' ismert változatban a palacsinták alja megégett, és a rendezés végén minden palacsintának az égett oldalával alul kell elhelyezkednie. Az '''égetett palacsinta-gráf''' ennek a problémának a gráf-reprezentációja: az ''előjeles permutációban'' ha az ''i'' palacsinta égett oldalával felfelé van, akkor a permutációban az ''i'' helyén az ''i`'' negatív elem szerepel. Erre a változatra David S. Cohen ([[David X. Cohen]]) és [[Manuel Blum]] 1995-ben a következő állítást igazolták: <math>3n/2\leq P'_n\leq 2n-2</math> (ahol a felső korlát csak <math>n>9</math>-től válik igazzá).<ref>David S. Cohen, Manuel Blum: ''On the problem of sorting burnt pancakes.'' In: ''Discrete Applied Mathematics.'' 61, Nr. 2, 1995, S. 105–120. [[DOI:10.1016/0166-218X(94)00009-3]].</ref> |
|||
{| class="wikitable" |
|||
|+ Égetett palacsinta-számok<br />{{OEIS|A078941}} |
|||
|<math>n</math> |
|||
| 1 || 2 || 3 || 4 || style="text-align:right" | 5 || style="text-align:right" | 6 || style="text-align:right" | 7 || style="text-align:right" | 8 || style="text-align:right" | 9 || 10 || 11 || 12 |
|||
|- |
|||
|<math>P'_n</math> |
|||
| 1 || 4 || 6 || 8 || 10 || 12 || 14 || 15 || 17 || 18 || 19 || 21 |
|||
|} |
|||
==Alkalmazásai== |
|||
A palacsintagráfok számos érdekes tulajdonsággal rendelkeznek – szimmetrikus és rekurzív szerkezetük ([[Cayley-gráf]]ok, ezért [[csúcstranzitív gráf|csúcstranzitívek]]), szublogaritmikus fokszámmal és átmérővel rendelkeznek és relatíve [[sűrű gráf|ritkák]] (pl. a [[hiperkockagráf]]okhoz képest), ezért a [[permutáló csillaggráf]]ok mellett a párhuzamos számítógépek hálózati összeköttetéseinek modelljeként komoly érdeklődés tárgyát képezik.<ref name="ongenus"/><ref>{{Cite journal|last=Akl|first=S.G.|last2=Qiu|first2=K.|last3=Stojmenović|first3=I.|date=1993|title=Fundamental algorithms for the star and pancake interconnection networks with applications to computational geometry.|url=http://onlinelibrary.wiley.com/doi/10.1002/net.3230230403|journal=Networks|volume=23|issue=4|pages=215–225|doi=10.1002/net.3230230403}}</ref><ref>{{Cite journal|last=Bass|first=D.W.|last2=Sudborough|first2=I.H.|date=2003-03|title=Pancake problems with restricted prefix reversals and some corresponding Cayley networks.|url=http://dx.doi.org/10.1016/S0743-7315(03)00033-9|journal=Journal of Parallel and Distributed Computing |volume=63|issue=3|pages=327–336|doi=10.1016/S0743-7315(03)00033-9}}</ref><ref>{{Cite journal|last=Berthomé|first=P.|last2=Ferreira|first2=A.|last3=Perennes|first3=S.|date=1996-12|title=Optimal information dissemination in star and pancake networks.|url=http://ieeexplore.ieee.org/document/553290/|journal=IEEE Transactions on Parallel and Distributed Systems|volume=7|issue=12|pages=1292–1300|doi=10.1109/71.553290}}</ref> Hálózati összeköttetések modelljeként tekintve a palacsintagráfokra, a gráf átmérője a kommunikációs késleltetést reprezentálja<ref>Kumar, V., Grama, A., Gupta, A., Karypis, G.: Introduction to Parallel Computing: Design and Analysis of Algorithms. Benjamin/Cummings (1994) </ref><ref>Quinn, M.J.: Parallel Computing: Theory and Practice, second edition. McGrawHill (1994)</ref>. |
A palacsintagráfok számos érdekes tulajdonsággal rendelkeznek – szimmetrikus és rekurzív szerkezetük ([[Cayley-gráf]]ok, ezért [[csúcstranzitív gráf|csúcstranzitívek]]), szublogaritmikus fokszámmal és átmérővel rendelkeznek és relatíve [[sűrű gráf|ritkák]] (pl. a [[hiperkockagráf]]okhoz képest), ezért a [[permutáló csillaggráf]]ok mellett a párhuzamos számítógépek hálózati összeköttetéseinek modelljeként komoly érdeklődés tárgyát képezik.<ref name="ongenus"/><ref>{{Cite journal|last=Akl|first=S.G.|last2=Qiu|first2=K.|last3=Stojmenović|first3=I.|date=1993|title=Fundamental algorithms for the star and pancake interconnection networks with applications to computational geometry.|url=http://onlinelibrary.wiley.com/doi/10.1002/net.3230230403|journal=Networks|volume=23|issue=4|pages=215–225|doi=10.1002/net.3230230403}}</ref><ref>{{Cite journal|last=Bass|first=D.W.|last2=Sudborough|first2=I.H.|date=2003-03|title=Pancake problems with restricted prefix reversals and some corresponding Cayley networks.|url=http://dx.doi.org/10.1016/S0743-7315(03)00033-9|journal=Journal of Parallel and Distributed Computing |volume=63|issue=3|pages=327–336|doi=10.1016/S0743-7315(03)00033-9}}</ref><ref>{{Cite journal|last=Berthomé|first=P.|last2=Ferreira|first2=A.|last3=Perennes|first3=S.|date=1996-12|title=Optimal information dissemination in star and pancake networks.|url=http://ieeexplore.ieee.org/document/553290/|journal=IEEE Transactions on Parallel and Distributed Systems|volume=7|issue=12|pages=1292–1300|doi=10.1109/71.553290}}</ref> Hálózati összeköttetések modelljeként tekintve a palacsintagráfokra, a gráf átmérője a kommunikációs késleltetést reprezentálja<ref>Kumar, V., Grama, A., Gupta, A., Karypis, G.: Introduction to Parallel Computing: Design and Analysis of Algorithms. Benjamin/Cummings (1994) </ref><ref>Quinn, M.J.: Parallel Computing: Theory and Practice, second edition. McGrawHill (1994)</ref>. |
||
A lap 2017. augusztus 3., 13:20-kori változata
| Palacsintagráf | |
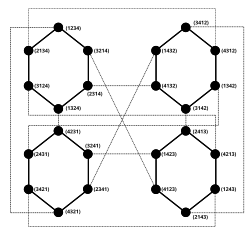 | |
| A P4 palacsintagráf rekurzívan előállítható a P3 4 kópiájából úgy, hogy az {1, 2, 3, 4} halmaz más-más elemét fűzzük hozzá az egyes kópiákhoz. | |
| Csúcsok száma | n! |
| Élek száma | n(n−1) |
| Átmérő | lásd a cikkben |
| Derékbőség | 6, ha n>2 |
| Kromatikus szám | lásd a cikkben |
| Génusz | lásd a cikkben |
| Egyéb | reguláris, Cayley-gráf, csúcstranzitív, nem éltranzitív, nem távolságtranzitív |
| Jelölés | |
A matematika, azon belül a gráfelmélet területén egy Pn palacsintagráf, avagy n-palacsintagráf olyan egyszerű, irányítatlan, hurokmentes gráf, melynek csúcshalmaza az 1,2,...,n számok permutációinak (sorbaállításainak) halmaza. Két permutáció között akkor húzódik él, ha az egyik tranzitív módon átvihető a másikba egy kezdőszeletének megfordításával (prefix reversal).
A palacsintarendezés (pancake sorting) az a matematikai probléma, melynek során különböző méretű palacsintákból álló oszlopot nagyság szerinti sorba rendeznek oly módon, hogy az oszlopba bárhol beszúrható egy fordítólapát, és az összes fölötte lévő palacsinta megfordítható vele. A palacsintarendezési probléma és a palacsintagráf átmérőjének meghatározása egymással ekvivalens.[1]
Az n méretű palacsintagráf, Pn rekurzívan előállítható a Pn−1 palacsintagráf n kópiájából oly módon, hogy az {1, 2, …, n} halmaz más-más elemét fűzzük hozzá az egyes kópiákhoz.
Tulajdonságai
A Pn palacsintagráf reguláris, csúcsainak száma n!, fokszáma n−1. Girthparamétere:
.
A Pn palacsintagráf γ(Pn) génuszáról elmondható, hogy[2]:
Átmérője
A palacsintarendezési probléma és a palacsintagráf átmérőjének („palacsintaszám”) meghatározása egymással ekvivalens.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| 0 | 1 | 3 | 4 | 5 | 7 | 8 | 9 | 10 | 11 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
A palacsintaszám, tehát az n palacsintát tartalmazó oszlop rendezéséhez mindig elégséges, minimális átfordítások száma és (kb. és ) között van, de a pontos érték nem ismert.[3]
1979-ben Bill Gates és Christos Papadimitriou[4] felső korlátot igazolt. Ezt 30 évvel később -re javította a University of Texas at Dallas egyetem Hal Sudborough által vezetett kutatócsoportja.[5] (Chitturi et al., 2009[6]).
2011-ben Laurent Bulteau, Guillaume Fertin és Irena Rusu[7] bebizonyították, hogy egy adott palacsintaoszlop rendezéséhez szükséges legrövidebb átfordítás-sorozat megtalálása NP-nehéz feladat.
Égetett palacsintagráf
Az égetett palacsinta-problémaként (burnt pancake problem) ismert változatban a palacsinták alja megégett, és a rendezés végén minden palacsintának az égett oldalával alul kell elhelyezkednie. Az égetett palacsinta-gráf ennek a problémának a gráf-reprezentációja: az előjeles permutációban ha az i palacsinta égett oldalával felfelé van, akkor a permutációban az i helyén az i` negatív elem szerepel. Erre a változatra David S. Cohen (David X. Cohen) és Manuel Blum 1995-ben a következő állítást igazolták: (ahol a felső korlát csak -től válik igazzá).[8]
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 4 | 6 | 8 | 10 | 12 | 14 | 15 | 17 | 18 | 19 | 21 |
Alkalmazásai
A palacsintagráfok számos érdekes tulajdonsággal rendelkeznek – szimmetrikus és rekurzív szerkezetük (Cayley-gráfok, ezért csúcstranzitívek), szublogaritmikus fokszámmal és átmérővel rendelkeznek és relatíve ritkák (pl. a hiperkockagráfokhoz képest), ezért a permutáló csillaggráfok mellett a párhuzamos számítógépek hálózati összeköttetéseinek modelljeként komoly érdeklődés tárgyát képezik.[2][9][10][11] Hálózati összeköttetések modelljeként tekintve a palacsintagráfokra, a gráf átmérője a kommunikációs késleltetést reprezentálja[12][13].
További információk
Jegyzetek
- ↑ Asai, Shogo (2006. szeptember 1.). „Computing the Diameter of 17-Pancake Graph Using a PC Cluster.”. Euro-Par 2006 Parallel Processing: 12th International Euro-Par Conference. DOI:10.1007/11823285_117.
- ↑ a b Nguyen, Quan (2009. november 5.). „On the Genus of Pancake Network.”. The International Arab Journal of Information Technology 8 (3), 289–292. o.
- ↑ Fertin, G. and Labarre, A. and Rusu, I. and Tannier, E. and Vialette, S.. Combinatorics of Genome Rearrangements. The MIT Press (2009). ISBN 9780262062824
- ↑ Gates, W. (1979). „Bounds for Sorting by Prefix Reversal”. Discrete Mathematics 27, 47–57. o. DOI:10.1016/0012-365X(79)90068-2.
- ↑ Team Bests Young Bill Gates With Improved Answer to So-Called Pancake Problem in Mathematics. University of Texas at Dallas News Center, 2008. szeptember 17. (Hozzáférés: 2008. november 10.) „A team of UT Dallas computer science students and their faculty adviser have improved upon a longstanding solution to a mathematical conundrum known as the pancake problem. The previous best solution, which stood for almost 30 years, was devised by Bill Gates and one of his Harvard instructors, Christos Papadimitriou, several years before Microsoft was established.”
- ↑ Chitturi, B. (2009. augusztus 31.). „An (18/11)n upper bound for sorting by prefix reversals”. Theoretical Computer Science 410 (36), 3372–3390. o. DOI:10.1016/j.tcs.2008.04.045.
- ↑ „Pancake Flipping Is Hard”. Journal of Computer and System Sciences 81, 1556–1574. o. DOI:10.1016/j.jcss.2015.02.003.
- ↑ David S. Cohen, Manuel Blum: On the problem of sorting burnt pancakes. In: Discrete Applied Mathematics. 61, Nr. 2, 1995, S. 105–120. DOI:10.1016/0166-218X(94)00009-3.
- ↑ Akl, S.G. (1993. május 20.). „Fundamental algorithms for the star and pancake interconnection networks with applications to computational geometry.”. Networks 23 (4), 215–225. o. DOI:10.1002/net.3230230403.
- ↑ Bass, D.W. (2003. március 1.). „Pancake problems with restricted prefix reversals and some corresponding Cayley networks.”. Journal of Parallel and Distributed Computing 63 (3), 327–336. o. DOI:10.1016/S0743-7315(03)00033-9.
- ↑ Berthomé, P. (1996. december 1.). „Optimal information dissemination in star and pancake networks.”. IEEE Transactions on Parallel and Distributed Systems 7 (12), 1292–1300. o. DOI:10.1109/71.553290.
- ↑ Kumar, V., Grama, A., Gupta, A., Karypis, G.: Introduction to Parallel Computing: Design and Analysis of Algorithms. Benjamin/Cummings (1994)
- ↑ Quinn, M.J.: Parallel Computing: Theory and Practice, second edition. McGrawHill (1994)












