Radardiagram
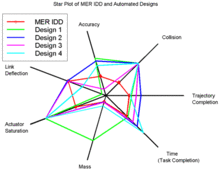
A radardiagram többváltozós adathalmazok kétdimenziós ábrázolására alkalmas. A külalakja miatt szokás pókháló-diagramnak is nevezni. Az ábrázolás során egy közös pontból egymáshoz képest azonos szögben hajló tengelyeket veszünk fel, majd a kvantitatív (számszerűen mérhető) mennyiségeket ezeken vesszük fel. A tengelyeket a rajtuk felvett értékek közötti kapcsolat alapján irányítjuk, azaz az egymással erősebben kapcsolt értékek egymáshoz közelebbi tengelyekre kerülnek. A pontok így egy síkidomot határoznak meg, ami a vizsgált jelenség vagy tulajdonság súlypontját is meghatározza.[1]
A diagramot ismerik még csillagdiagram,[2] pókdiagram és Kiviat diagram[3][4] néven is. A diagram egyenértékű a párhuzamos koordinátákkal, csak itt a tengelyek sugárirányúak.
Áttekintés[szerkesztés]
A radardiagramot egy közös pontból kiágazó, egyenlő hajlásszögű küllők, sugarak alkotják. A sugarak hossza arányos az adatérték és a maximális érték hányadosával. Ilyen módon a diagramnak nevet is adó csillagszerű síkidomot kapunk. Ez még inkább látványossá válik, amikor a pontokat egyenes vonalakkal összekötjük. Egy ilyen módon felvett sokszög alapján az alábbi kérdésekre adunk választ:[5]
- Mely megfigyelések hasonlóak?
- Vannak-e megfigyelési klaszterek, azaz közös részei a megfigyeléseknek?[5]
- Vannak-e kívülállók?
A radardiagramot általában sokváltozós megfigyelések ábrázolására használjuk, tetszőlegesen sok változó figyelembe vételével. Egy-egy diagramon általában sok csillagot veszünk fel, minden egyes csillag egy-egy megfigyelést jelképez.[5] Ilyen ábrát először Georg von Mayr használt 1877-ben.[6][7] A radardiagram annyiban különbözik a glifa diagramtól, hogy minden változót felhasználunk, és nem különböztetjük meg a fő és mellékváltozókat. Különösen jól használhatóak, ha a küllőket valamilyen szempont szerint csoportosítjuk.[8]
Alkalmazások[szerkesztés]
Gyakran a minőségfejlődés mérésére alkalmazzák a minőségirányításban.[9]
A sportolók esetén a játékosok erősségeit és gyengeségeit ábrázolják ilyen módon. [10]
Korlátai[szerkesztés]
A radardiagramoknak kifejezetten szerepe van a közös területek és a kiugróság mérésében, valamint alkalmazhatóak az ordinális mérésekben, amikor a változók bizonyos szempontból "jobbak", mint mások, és egyforma skálázással bírnak.
A radardiagramok fő problémája, hogy nem alkalmasak kompromisszumos megállapodások meghozására, amikor egy diagram nagyobb értékű a többinél valamely változóban, de a többiben nem.[11]
A diagramokat nehéz vizuálisan értelmezni, mivel a sugárirányú távolságokat a szem nehezebben becsüli. Erre a problémára megoldás lehet a koncentrikus körök van összekötő egyenesek alkalmazása, amik miatt a pókháló diagram megnevezést is kapta.[12]
A diagram torzítja az adatokat is a kitöltött síkidom révén, ugyanis így a terület az adatok második hatványával arányos. Például vegyünk egy öt változós mérést, amikor a változók értéke 1-100-ig terjed. Ha egy mérésben minden érték 90, egy másikban pedig 82, az első síkidom területe több, mint 20%-kal nagyobb a másodikénál, holott a változók aránya alatta van a 10%-nak.
Felépítés[szerkesztés]
A radardiagramok az adatokat gyakran mesterséges rendszerbe sorolják, amik a diagram értelmezését megváltoztathatják.
- Szomszédsági viszonyok: Ezek nem mindig jelentenek kapcsolatot az egyes sugarak adatai között, viszont könnyen sugalmazhatnak ilyet.
- Körkörös szerkezet: Az első és utolsó adattípus egymás mellé kerül.
- Hosszúság: Az adatok rendszerint rendezettek, de a fokozatok mesterségesek.
- Területi torzítás: A kiugró adatok túlreprezentáltak lesznek, mivel a terület a lineáris méretek második hatványával arányos. A (2;2) négyzet területe az (1;1) négyzetének négyszerese, holott az adatok csak kétszeres viszonyt mutatnak. Ez a becslés torzulását okozza.[13]
Például a (9; 1; 9; 1; 9; 1) adatsor egy csillagszerű alakzat a radardiagramot, azonban ha sorba rendezzük ezeket, akkor a kapott (9; 9; 9; 1; 1; 1) adatsor diagramja már csak két különböző sugarú szeletet fog jelenteni. A kettő között a döntés nem mindig kézenfekvő, és esetleg az értelmezés mesterséges irányítását lehetővé teszi.
Egyes esetekben azonban a radardiagram teljesen természetesen használható. Ilyen például a ciklikus adatok ábrázolása, például a naponta, óránkénti rendszerességű adatfelvétel. Ekkor a sugaraknak is van természetes rendszere, a ciklikusság miatt pedig a körkörös szerkezet nem hiba, hanem a természetes viselkedés.[12][14][15]
Mikor érdemes radardiagramot alkalmaznunk?[15]
- Ha értelmezhetőek a területek közös skálázás nélkül is.
- Ha az adathalmaz valóban ciklikus, nem lineáris.
- Legalább két összehasonlítandó adatsor van, és az egyik lényegesen kisebb a másiknál.
Adathalmaz mértéke[szerkesztés]
A radardiagram segíti a sokváltozós kicsi és közepes adatok elemzését. A fő gyengeségét is pont ez jelenti: ha pár száz pontnál többet kell ábrázolni, a diagram áttekinthetetlenné válik. [5]
Példa[szerkesztés]

Jobbra néhány autómárka radardiagramja[5] látható. Az egyes tengelyek tartalma:
- Ár
- Futásteljesítmény
- Szervízelés 1978
- Szervízelés 1977
- Belmagasság
- Hátsó üléstér
- Csomagtartó
- Tömeg
- Hossz
A diagramokat tekinthetjük egyénenként és egy-egy csoport hasonló autó összehasonlításakor is. Például nézzük a Cadillac Sevilla márka diagramját (Az utolsó ábra a jobb oldali képen)! Eszerint az autó a legdrágábbak egyike, a futásteljesítménye átlag alatti, a szervizelése átlagos és az átlagosnál kicsit jobb a belső tere.
Ha a Cadillac autóit (utolsó három ábra) az AMC gyártóéival (első három diagram) hasonlítjuk össze, akkor egészen más következtetésekre juthatunk. AZ AMC gyártmányú járművek olcsók, viszont átlag alatti a futásteljesítményük és minden tekintetben kicsik. A Cadillacek drágák, rossz a futásteljesítményük, viszont tágas tér és nagy tömeg jellemzi őket.[5]
Alternatívák[szerkesztés]
Főleg idődiagramok esetén inkább használjunk egyszerű vonaldiagramot.
Kétdimenziós összehasonlításokra sokkal alkalmasabbak a Harvey labdák.[16] Ezeket jelentősen segíti, hogy algoritmikusan lehet sorrendet kialakítani.[17]
A főkomponens-analízis egy nagyszerű módszer a többváltozós adatstruktúrák elemzésekor.
A törött vonal helyett használhatunk kis oszlopokat az egyes tengelyek mentén.[17]
Habár a poláris diagramok és a radardiagramok sokszor egyként vannak tekintve,[4] a kettő között lényegi különbség van, ugyanis a radardiagram az adatokat nem polárkoordinátákban ábrázolja.[18]
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Radar chart című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek[szerkesztés]
- ↑ (2018. április 25.) „Multidimensional mechanics: Performance mapping of natural biological systems using permutated radar charts”. PLOS ONE 13 (9), e0204309. o. DOI:10.1371/journal.pone.0204309. PMID 30265707.
- ↑ Nancy R. Tague (2005) The quality toolbox. page 437.
- ↑ (1973. április 25.) „The Software Empiricist”. ACM SIGMETRICS Performance Evaluation Review 2 (2), 31–36. o. DOI:10.1145/1113644.1113647. „Dr. Philip J. Kiviat azt ajánlotta legutóbbi NBS/ACM megbeszélésen, hogy a körkörös grafikon sugárirányú változótengelyekkel hasznos alak lenne. [...] Javaslom ezek "Kiviat ábra" vagy "Kiviat grafikon" névvel illetését, hogy a javaslata fontosságát kihangsúlyozzuk.”
- ↑ a b Find Content Gaps Using Radar Charts. Content Strategy Workshops, 2015. március 3. [2020. augusztus 6-i dátummal az eredetiből archiválva]. (Hozzáférés: 2015. december 17.)
- ↑ a b c d e f NIST/SEMATECH (2003). Star Plot in: e-Handbook of Statistical Methods. 6/01/2003 (Date created)
- ↑ Mayr, Georg von (1877), Die Gesetzmäßigkeit im Gesellschaftsleben, Munich: Oldenbourg, p.78. Linien-Diagramme im Kreise: Line charts in circles.
- ↑ Michael Friendly (2008). "Milestones in the history of thematic cartography, statistical graphics, and data visualization" Archiválva 2018. szeptember 26-i dátummal a Wayback Machine-ben.
- ↑ Michael Friendly (1991). "Statistical Graphics for Multivariate Data". Paper presented at the SAS SUGI 16 Conference, Apr, 1991.
- ↑ Ron Basu (2004). Implementing Quality: A Practical Guide to Tools and Techniques. p.131.
- ↑ Spider Graphs: Charting Basketball Statistics
- ↑ You are NOT spider man, so why do you use radar charts?, by Chandoo, September 18th, 2008
- ↑ a b Peltier, Jon: Rock Around The Clock - Peltier Tech Blog. Peltiertech.com, 2008. augusztus 14. (Hozzáférés: 2013. szeptember 11.)
- ↑ (Cleveland 1984), summarized at http://processtrends.com/toc_data_visualization.htm Archiválva 2010. március 25-i dátummal a Wayback Machine-ben.
- ↑ Charting around the clock The Excel Charts Blog. Excelcharts.com, 2008. augusztus 15. (Hozzáférés: 2013. szeptember 11.)
- ↑ a b Clock This
- ↑ Qualitative Comparison. Support Analytics Blog , 2007. december 11. [2012. április 8-i dátummal az eredetiből archiválva].
- ↑ a b Information Ocean: Reorderable tables II: Bertin versus the Spiders. I-ocean.blogspot.com, 2008. szeptember 24. (Hozzáférés: 2013. szeptember 11.)
- ↑ Polar Charts (Report Builder and SSRS). Microsoft Developer Network. (Hozzáférés: 2015. december 17.)
