Kivonás

"5 ‒ 2 = 3" (ötből kettő egyenlő három)

A kivonás a számtani alapműveletek egyike. Az összeadás megfordítása. Ez azt jelenti, hogy ha az a számhoz hozzáadjuk a b számot, majd az összegből kivonjuk a b számot, akkor visszakapjuk az a számot. A kivonás jele a - mínusz jel.

A c − b = a kivonásban c a kisebbítendő, b a kivonandó, és a a különbség.

A matematikában gyakran hasznos a kivonást egyfajta összeadásnak tekinteni, és az összeadással együtt összevonásról beszélni. A kivonás ugyanis felfogható az ellentett hozzáadásaként. Így alkalmazhatók az összeadás tulajdonságai.

Hagyományos tárgyalásban a kivonás

• nem kommutatív, hanem antikommutatív
• nem asszociatív

A szorzás disztributív a kivonásra. Az osztás jobbról disztributív a kivonásra.

A kivonás többféleképpen is bevezethető:

1. Tárgyak egy halmazából elveszünk egy adott számú elemet. Például 5 barackból elveszünk 2 barackot, marad 3 barack (természetes számok).

2. Egy adott mértékű halmazból elveszünk egy adott mennyiséget ugyanabban a mértékegységben mérve. Például kimérünk 200 grammot, és elveszünk belőle 10 grammot, akkor marad 190 gramm (pozitív számok).

3. Két mennyiség összehasonlítása. Például 800 Ft és 600 Ft különbsége 800 Ft − 600 Ft = 200 Ft (valós számok).

A kivonás és az egész számok bevezetése

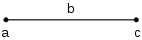
Vegyünk egy szakaszt, aminek kiindulópontja a, és hossza b. Jelöljük a szakasz másik végpontját c-vel. Az a pontból kiindulva b lépéssel érünk c-be:

a + b = c.

A c pontból b lépést kell visszamenni, hogy a-ba jussunk:

c − b = a.

A természetes számok nem zártak a kivonásra: ha egy kisebb számból akarunk kivonni egy nagyobbat, akkor nem kapunk eredményt a természetes számok halmazán. Ahhoz, hogy bármely kivonást el lehessen végezni, a számkört bővíteni kell a negatív számokkal, és ha a pozitív egészeket vettük a természetes számoknak, akkor a 0 számot is hozzá kell venni az eddigi számkörhöz. Ezzel az egész számokhoz jutunk.

Tekintsük az egész számok számegyenesét:

(…, ‒3, ‒2, ‒1, 0, 1, 2, 3, …)

Innen a 3-ból 4-et lépve vissza a -1-hez jutunk:

3 ‒ 4 = ‒1.

Algoritmusok

Többféle kivonási algoritmus létezik. Többféle módszert alkalmaznak a kézi számításokhoz.

Egy elterjedt módszer szerint az a_j a_j‒1 … a₀ kisebbítendőből így vonják ki a b_k b_k‒1 … b₀ kivonandót:

Minden egyes i-re az a_i jegyből kivonják a megfelelő b_i-t. Ha a_i kisebb, mint b_i, akkor a_i-t megnövelik tízzel, és a következő nagyobb helyiértékű jegyet: az amerikai módszer szerint a kisebbítendő jegyét csökkentik eggyel, az európai módszer szerint a kivonandó jegyét növelik eggyel.

Példa

A 704 − 512 kivonásban 704 a kisebbítendő, és 512 a kivonandó. A kisebbítendő jegyei a₂=7, a₁=0, a₀=4. A kivonandó jegyei b₂=5, b₁=1, b₀=2. Az egyesektől kezdve 4 nem kisebb 2-nél, ezért 4-2=2 lesz a különbség utolsó jegye. A tízesek helyén 0 kisebb, mint 1, ezért a 0 jegyhez hozzáadunk 10-et; így 10-1=9 lesz a különbség tízes helyiértékű jegye.

Az amerikai módszer eggyel csökkenti a kisebbítendő következő jegyét, tehát áthúzza a 7-et, és 6-ot ír. A kivonás a százas helyiértéken folytatódik. A 6 nem kisebb, mint 5, ezért 6-5=1 lesz a különbség százas helyi értékű jegye. A kisebbítendőnek nincs több jegye, ezért a kivonás véget ér. A különbség eszerint 192.

Az Európában is alkalmazott ausztrál módszer egyet ad hozzá a kivonandó következő jegyéhez. Ezt a jegyet meg is jelöli egy kis jellel. A kivonás következő lépésében az a kérdés, hogy melyik számhoz kell hozzáadni 5-öt és még egyet, hogy 7-et kapjunk. A válasz 1, és ez lesz a különbség száz helyi értékű jegye.

Számítógépek

Egész számok között nincs igazi különbség az összeadás és a kivonás között, mivel általában a számítógépek kettes komplemensben ábrázolják a negatív számokat, így a kivonás gyakorlatilag túlcsordulásos összeadás.

Lebegőpontos számokon a számítógép kivonási módszere az ellentett hozzáadásán alapul. A lebegőpontos számokkal pontosan elvégzi a műveletet, majd a különbséghez hozzárendeli a legközelebbi lebegőpontos számot.

Az azonos előjelű számok kivonásának speciális hibája a vészes kiegyszerűsödés. Ennek az az oka, hogy a keretből kicsúszott jegyeket azonnal elfelejti. Az értékes számjegyek eltűnnek; ezzel döntő információ veszhet el. Ez a hiba leginkább akkor jelentkezik, ha a különbség kicsi. A számítógép akár egy egész nagyságrendet is tévedhet. A vészes kiegyszerűsödés miatt a kivonás nagyon rosszul kondicionált, inkorrekt művelet.

A vészes kiegyszerűsödés ellen tartalék számjegyekkel lehet védekezni.

Források

• Browell, W. A. (1939). Learning as reorganization: An experimental study in third-grade arithmetic, Duke University Press.
• Subtraction in the United States: An Historical Perspective, Susan Ross, Mary Pratt-Cotter, The Mathematics Educator, Vol. 8, No. 1 (original publication) and Vol. 10, No. 1 (reprint.) https://web.archive.org/web/20170811133911/http://math.coe.uga.edu/tme/issues/v10n2/5ross.pdf

Külső hivatkozások

Printable Worksheets: One Digit Subtraction, Two Digit Subtraction, and Four Digit Subtraction

• Subtraction Game at cut-the-knot
• Subtraction on a Japanese abacus selected from Abacus: Mystery of the Bead