Bináris kupac

Bináris kupac
Típus	Fa
Komplexitás (O jelöléssel)
Tárigény	O(n)
Beszúrás	Θ(log n)
Törlés	Θ(log n)

A bináris kupac egy kupac adatszerkezet, mely a d-kupac egy speciális esete, ahol d=2 - azaz egy olyan kupac, ami egy bináris fa, amelyre teljesül két újabb megkötés:

• Teljesség: A bináris kupac egy teljes bináris fa, azaz a fa minden szintje, kivéve esetleg az utolsó szintet, fel van töltve adatokkal, és amennyiben az utolsó szint nem teljes, az balról jobbra van részben feltöltve.
• Kupactulajdonság: A bináris kupacban A csúcs és annak B leszármazottja között fennáll, hogy (maximum kupac esetén) kulcs(A) ≥ kulcs(B), vagy (minimum kupac esetén) kulcs(B) ≥ kulcs(A).
  

Műveletek

A bináris kupacban a kupac alapvető műveleteit értelmezzük. A bináris kupac egyes műveleteinek leírásához C példakódot is megadtunk, amely a következő struktúrát használja:

typedef struct Kupac {
    int *tomb;
    int meret;
    int kapacitas;
} Kupac;

A példákban a bináris kupacot tömb formájában implementáljuk, ezt bővebben az Implementáció szakaszban fejtjük ki. A struktúrán felül szükségünk van egy tömböt bővítő függvényre, amely a tömböt átméretezi, ha az betelik, valamint egy cserélő függvényre, amely két elemet megcserél.

void bovit(Kupac *kupac)
{
    int *tomb = malloc(2 * kupac->kapacitas * sizeof(int));
    for (int i = 0; i < kupac->kapacitas; i++) {
        tomb[i] = kupac->tomb[i];
    }
    free(kupac->tomb);
    kupac->tomb = tomb;
    kupac->kapacitas *= 2;
}

void cserel(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

A továbbiakban minden művelet leírása egy bináris max-kupacra vonatkozik. Min-kupac esetén a relációk megfordulnak.

Beszúrás

A kupacba való beszúráskor az elemet először a következő helyre rakjuk (azaz amennyiben a fa legalsó szintje nem teljes, akkor a szinten balról jobbra haladva a következő szabad helyre, ha pedig teljes, akkor a következő szint bal szélső elemeként szúrjuk be). Ezután megvizsgáljuk, hogy az új elem nagyobb-e, mint a közvetlen felmenője. Ha igen, megcseréljük. Ezt addig ismételjük, amíg az új felmenő nagyobb nem lesz, mint az elem, vagy az új elem a gyökérelem helyére kerül. Ezt a folyamatot up-heap-nek, azaz felfelé kupacosításnak hívjuk. A legrosszabb esetben az új elem a gyökérelem, azaz egy összehasonlításra és cserére van szükségünk minden szinten, tehát a beszúrás lépésszáma O(log n). Azonban, mivel az elemek 50%-a levélelem, és átlagosan 75%-uk a legalsó két szinten helyezkedik el, a beszúrás átlagos lépésszáma O(1). A lépésszámok nem veszik figyelembe a tömb átméretezésének költségét, azonban a tömb hatékony kezelése esetén azt mondhatjuk, hogy a beszúrás amortizált lépésszáma O(log n).

A beszúrásra kódrészlet:

void felfele_kupacosit(Kupac *kupac)
{
    int i = kupac->meret - 1;
    int j = (i - 1) / 2; // szülő
    while (i > 0 && kupac->data[i] > kupac->data[j]) {
        cserel(&kupac->data[i], &kupac->data[j]);
        i = j;
        j = (i - 1) / 2;
    }
}

void beszur(Kupac *kupac, int ertek)
{
    if (kupac->meret == kupac->kapacitas) {
        bovit(kupac); // ha a tömb betelik
    }
    kupac->tomb[kupac->meret++] = ertek;
    felfele_kupacosit(kupac);
}

Törlés

Max-kupacból való törlés alatt a max-törlés műveletet értjük, azaz a maximum elem eltávolítását a kupacból. A törlés során először megcseréljük a gyökérelemet (azaz a maximum elemet) a kupac utolsó elemével (azaz a legalsó szint jobb szélső elemével), majd az így kapott levelet eltávolítjuk. A fa új gyökéreleme ekkor lehetséges, hogy nem a legnagyobb elem a fában, így a down-heap azaz lefelé kupacosítás műveletét alkalmazzuk: Ha ez az elem kisebb, mint valamely leszármazottja, megcseréljük az elemet a nagyobbik leszármazottjával, és ezt addig folytatjuk ezzel az elemmel, amíg mindkét leszármazottja kisebb nem lesz nála. Mivel mindig a nagyobbik leszármazottjával cseréltük meg, a kupactulajdonság nem sérülhetett, hiszen a helyére mindig nagyobb elem került. Így a kupac helyreáll. Legrosszabb esetben ezt az elemet a legalsó szintig le kell süllyeszteni, tehát összesen O(log n) a törlés lépésszáma.

Példakód törlésre:

void lefele_kupacosit(Kupac *kupac)
{
    int i = 0;
    for (;;) {
        int bal = 2 * i + 1, jobb = 2 * i + 2; // bal és jobb gyerek
        int max = (jobb < kupac->meret && kupac->tomb[jobb] > kupac->tomb[bal]) ? jobb : bal;
        if (bal >= kupac->meret || kupac->tomb[i] > kupac->tomb[max])
            break;
        cserel(&kupac->tomb[i], &kupac->tomb[max]);
        i = max;
    }
}

int maximum_torol(Kupac *kupac)
{
    cserel(&kupac->tomb[0], &kupac->tomb[--kupac->meret]);
    lefele_kupacosit(kupac);
    return kupac->tomb[kupac->meret];
}

Implementáció

Bináris fa tömbben

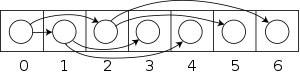
A bináris kupacok implementálása gyakran tömbökkel történik a más, bináris fa szerkezetű adatszerkezetek helyett. Ennek magyarázata az, hogy mivel a bináris kupac teljes bináris fa, tömbben kevesebb helyet foglal, mivel nincs szükség mutatók tárolására. A bináris kupac tömbös implementációja egy implicit adatszerkezet - azaz nincs szükségünk O(1)-nél több adat tárolására, mint maguk az adatszerkezet elemei. Tömbbel való implementációkor kétféleképpen határozhatjuk meg a gyökérelem helyét:

• Ha a gyökérelem a 0. indexre helyezzük, akkor felesleges helyfoglalást nem végzünk, de bonyolultabb a hozzátartozók meghatározása: egy adott i indexű elem leszármazottai 2i+1 és 2i+2, felmenője pedig (i-1)/2 alsó egészrésze. Ezt a tárolási módot alkalmaztuk a fenti példakódokban is.
• Ha a gyökérelem az 1. indexű, akkor a 0. indexen egyéb hasznos adatot tárolhatunk (pl. tömb mérete). A hozzátartozók meghatározása is egyszerűbb: i leszármazottai 2i és 2i+1, felmenője pedig i/2 alsó egészrésze.

A bináris kupacokat implementálhatjuk a szokásos bináris faszerkezetként is, de ekkor bonyolultabb a szomszédos elemek meghatározása.

Kapcsolódó szócikkek

• Bináris fa