Vékonyréteg
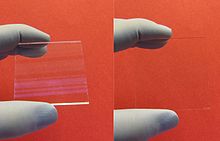
A fizikában és kémiában vékonyrétegnek nevezik az anyag kis vastagságú tartományait, melyek az atomi méretektől a néhány mikrométerig terjedő méretűek. Leggyakoribb alkalmazásaik az optikai bevonatok és a félvezetőiparban alkalmazott elektromos vékonyrétegek.
Közismert, hétköznapokban is gyakori alkalmazásuk a tükör, mely egy üveg hordozóból és a rá felvitt fém (gyakran ezüst) vékonyrétegből áll. Igen vékony bevonattal féligáteresztő tükör is készíthető.
A vékonyrétegek fizikai jellemzése a szilárdtestfizika, ezen belül a felületfizika tárgykörébe tartozik. Egyes vékonyrétegek (főleg melyek vastagsága közel esik az atomi méretekhez) bizonyos alkalmazások esetén kvázi kétdimenziós szerkezetként viselkednek, melyet kvantumbezárási effektusok okoznak.
Előállítása
Vékonyréteg-leválasztásnak[m 1] azt a folyamatot nevezik, amikor fizikai vagy kémiai reakció segítségével egy anyag (hordozó) felületén, mikro- vagy nanotechnológiai eljárással vékonyréteg épülését idézik elő. A réteg épülése tipikusan néhányszor tíz-száz nanométeres mérettartományon kontrollálható, de például molekulasugaras epitaxiával atomi rétegek is leválaszthatók.
A rétegleválasztási eljárások két alapvető kategóriába sorolhatók. A vékonyréteg létrejöttét meghatározó folyamat szerint megkülönböztetnek kémiai és fizikai elvű rétegleválasztásokat.[1]
Rétegnövekedési módok

A rétegek növekedését megszabják a felületi energiaviszonyok, azaz hogy a hordozó felülete és a kapcsolódó új atomok (adatom) között milyen a kölcsönhatás, illetve miként hatnak kölcsön egymással a leválasztott réteg atomjai. Eszerint három jellemző alapesetet különböztetnek meg:[2]


- Frank–van der Merwe-folyamat,[3][4][5] azaz rétegenkénti növekedés. Ebben az esetben az adatom-felület kölcsönhatás és az adatom-adatom kölcsönhatás kiegyensúlyozza egymást. Szükséges hozzá a rácsilleszkedés, melyen ideális rétegnövekedés lehetséges.
- Stranski–Krastanov-folyamat,[6] azaz összenövő szigetekben növekedés. Ez akkor jellemző növekedési mód, ha az adatom-felület kölcsönhatások dominálnak.
- Volmer–Weber-folyamat,[7] azaz izolált szigetek növekedése. Ekkor a réteg atomjai közötti kölcsönhatások dominálnak, így az atomok "cseppekbe", "szigetekbe" rendeződnek.
Epitaxia
Egy anyag egy rétegének a ránövése egy másik anyag egyetlen kristályára úgy, hogy a kristályszerkezet a rétegben azonos a szubsztrátéval. Félvezető eszközök készítésénél alkalmazzák.[8]
Alkalmazások
Források
- M. Birkholz, with contributions by P.F. Fewster and C. Genzel. Thin Film Analysis by X-Ray Scattering. Weinheim: Wiley-VCH (2005). ISBN 978-3-527-31052-4 Table of contents
- M. Ohring. Materials Science of Thin Films, 2nd, Boston: Academic Press (2001). ISBN 9780125249751
- K. Seshan, ed.. Handbook of Thin Film Deposition, 3rd, Amsterdam: Elsevier (2012). ISBN 978-1-4377-7873-1
- D.M. Mattox. The Foundations of Vacuum Coating Technology. Norwich: Noyes / William Andrew Publishing (2003). ISBN 0-8155-1495-6
- Giber János és szerzőtársai: Szilárdtestek felületfizikája. Budapest: Műszaki Könyvkiadó. 1987. ISBN 9789631071115
Fordítás
Ez a szócikk részben vagy egészben a Thin film című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Megjegyzések
- ↑ A magyar rétegleválasztás szakkifejezés gyakran félreértésre ad okot: a leválasztás itt a mintadarab felületére történik, azaz a réteg épülésével jár, nem pedig onnan egy réteg eltávolításával.
Hivatkozások
- ↑ Functional Polymer Films Eds.
- ↑ Grabow, M. H., & Gilmer, G. H. (1988). Thin film growth modes, wetting and cluster nucleation. Surface science, 194(3), 333-346.
- ↑ Frank, F. C. (1949. november 5.). „One-Dimensional Dislocations. I. Static Theory”. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 198 (1053), 205–216. o. DOI:10.1098/rspa.1949.0095. JSTOR 98165.
- ↑ Frank, F. C. (1949. november 5.). „One-Dimensional Dislocations. II. Misfitting Monolayers and Oriented Overgrowth”. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 198 (1053), 216–225. o. DOI:10.1098/rspa.1949.0096. JSTOR 98166.
- ↑ Frank, F. C. (1949. november 5.). „One-Dimensional Dislocations. III. Influence of the Second Harmonic Term in the Potential Representation, on the Properties of the Model”. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 200 (1060), 125–134. o. DOI:10.1098/rspa.1949.0163. JSTOR 98394.
- ↑ Stranski, I. N. (1938. november 5.). „Zur Theorie der orientierten Ausscheidung von Ionenkristallen aufeinander”. Sitzungsber. Akad. Wiss. Wien. Math.-Naturwiss. 146, 797–810.. o.
- ↑ Volmer, M. (1926. november 5.). „Keimbildung in übersättigten Gebilden”. Z. Phys. Chem 119, 277–301. o.
- ↑ Kémiai kislexikon, Typotex, 2007, epitaxia
