Maximális áramlási probléma

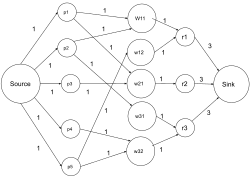
Az optimalizálási elméletben a maximális áramlási problémák magukban foglalják egy megvalósítható áramlás megtalálását olyan áramlási hálózaton keresztül, amely a lehető legnagyobb áramlási sebességet érheti el.

A maximális áramlási problémát a bonyolultabb hálózati áramlási problémák, például a forgalmi probléma különleges esetének tekinthetjük. Egy s-t folyam maximális értéke (azaz az áramlás az s forrástól a t süllyedésig) megegyezik az s-t vágás (azaz az s-t a t-től elválasztó vágás) minimális kapacitása értékével a hálózatban, ahogyan az a Maximális folyam – minimális vágás tétel állítja.

Történet[szerkesztés]

A maximális áramlási problémát T. E. Harris és F. S. Ross 1954-ben fogalmazta meg először a szovjet vasúti forgalom egyszerűsített modelljeként.^[1]^[2]^[3]

1955-ben Lester R. Ford, Jr. és Delbert R. Fulkerson elkészítette az első ismert algoritmust, a Ford–Fulkerson-algoritmust.^[4]^[5] 1955-ben írt cikkükben Ford és Fulkerson írta, hogy Harris és Ross problémáját a következőképpen fogalmazzák meg (lásd:^[1] 5. o.):

Vegyünk egy vasúthálózatot, amely összeköt két várost több közbülső város útján, ahol a hálózat mindegyik összeköttetése egy számmal rendelkezik, amely a kapacitását jelöli. Állandó állapot feltételezve keresse meg a maximális áramlást az adott városból a másikba.

A Flows in Network című könyvében^[5] 1962-ben a Ford és Fulkerson írta:

A szerzőknek 1955 tavaszán terjesztette elő, TE Harris, aki az FS Ross tábornokkal együtt kidolgozta a vasúti forgalom egyszerűsített modelljét, és ezt a problémát a központi javaslat szerint jelölte meg. modell [11].

ahol [11] utal a Harris és Ross által a vasúti hálózati kapacitások értékelési módszerének alapjaira vonatkozó 1955-es titkos jelentésre^[3] (lásd ^[1] 5. o.).

Az évek során különféle továbbfejlesztett megoldásokat fedeztek fel a maximális áramlási problémára, nevezetesen Edmonds és Karp, valamint önállóan Dinitz legrövidebb kiterjesztési útjának algoritmusát; Dinitz blokkoló áramlási algoritmusa; Goldberg és Tarjan push-relabel algoritmusa; valamint Goldberg és Rao bináris blokkoló áramlási algoritmusa. Az algoritmusok Sherman^[6] és Kelner, Lee, Orecchia és Sidford,^[7]^[8] keressen egy megközelítőleg optimális maximális áramlást, de csak irányítatlan grafikonokban dolgozzon.

2013-ban James B. Orlin kiadott egy, a $O(|V||E|)$ algoritmus minden értékére $|V|$ és $|E|$ .^[9]

Meghatározás[szerkesztés]

Áramlási hálózat, forrásokkal és végpontokkal. Az él melletti számok a kapacitások

Létrehozza $N=(V,E)$ hálózatot az $s,t\in V$ a forrás és végpontok $N$ -et illetőleg.

Egy él kapacitásának leképezése

c:E\to \mathbb {R} ^{+}

, jelölve

c_{uv}

vagy

c(u,v)

. Ez az áramlás maximális mennyiségét jelöli, amely áthaladhat az élen.

Az áramlás egy leképezés

f:E\to \mathbb {R} ^{+}

, jelölve

f_{uv}

vagy

f(u,v)

, a következő két korlátozással:

$f_{uv}\leq c_{uv}$ , az egyes $(u,v)\in E$ (kapacitáskorlátozás: egy él áramlása nem haladhatja meg a kapacitását);
$\sum _{u:(u,v)\in E}f_{uv}=\sum _{u:(v,u)\in E}f_{vu}$ , az egyes $v\in V\setminus \{s,t\}$ (áramlások megőrzése: a csomópontba belépő áramlások összegének meg kell egyeznie a csomópontból kilépő áramlások összegével, kivéve a forrást és a végpontok csomópontjait).

Az áramlás a ferde szimmetriát is megfigyeli

f_{uv}=-f_{vu}

, az egyes

(u,v)\in E

Az áramlás értékét az alábbiak határozzák meg:

|f|=\sum _{v:(s,v)\in E}f_{sv}

, ahol

s

a forrása

N

. A forrástól a végponthoz vezető áramlás mennyiségét jelzi.

A maximális áramlási probléma a maximalizálás $|f|$ , azaz a lehető legnagyobb mennyiségű áramlást kell átirányítani $s$ -nek a $t$ -re.

Megoldások[szerkesztés]

Az alábbi táblázat algoritmusokat sorol fel a maximális áramlási probléma megoldására.

Eljárás	Bonyolultság	Leírás
Lineáris programozás		A legal flow meghatározása által megadott korlátozások. Lásd a lineáris programot itt.
Ford – Fulkerson algoritmus	$O (E max\| f \|)$	Mindaddig, amíg a maradék gráfon keresztül nyitott az út, elküldi a maradék kapacitások minimumát. Az algoritmus csak akkor záródik le, ha minden súly racionális. Egyébként előfordulhat, hogy az algoritmus nem konvergál a maximális értékre. Ha azonban az algoritmus lezárul, akkor garantáltan megtalálja a maximális értéket.
Edmonds – Karp algoritmus	$O (VE 2)$	A Ford – Fulkerson specializációja, kiterjesztő utak megtalálása breadth-first kereséssel.
Dinic's blokkoló áramlási algoritmusa	$O (V 2 E)$	Az algoritmusok mindegyik fázisban réteges gráfot építnek fel, a breadth-first keresésével a maradék gráfra. A réteges gráfban a maximális áramlás $O (VE)$ időben kiszámítható, a fázisok maximális száma $V -1$ . Az egységkapacitással rendelkező hálózatokban a Dinic's algoritmusa befejeződik $O(\min\{V^{2/3},E^{1/2}\}E)$ idő.
MPM (Malhotra, Pramodh-Kumar és Maheshwari) algoritmus^[10]	$O (V 3)$	Csak aciklikus hálózatokon működik. Lásd az Original Paper.
Dinic's algoritmusa	$O (VE log(V))$	A dinamikus fák adatszerkezete felgyorsítja a rétegezett grafikon maximális áramlási számítását $O (V E log(V))$ .
General push-relabel maximális áramlási algoritmus	$O (V 2 E)$	A push relabel algoritmus fenntart egy preflow-t, azaz egy flow-függvényt a csúcsok feleslegének lehetőségével. Az algoritmus akkor fut, ha van egy csúcs, ahol pozitív többlet van, azaz aktív csúcs a grafikonon. A push művelet növeli az áramlást egy maradék szélen, és a csúcsok magasságfüggvénye szabályozza, hogy melyik maradék élek lehetnek tolhatók. A magasság funkciót egy relabel művelettel kell megváltoztatni. Ezeknek a műveleteknek a megfelelő meghatározása garantálja, hogy a kapott áramlási funkció maximális áramlást eredményez.
Push-relabel algoritmus <i id="mwtA">FIFO</i> csúcsválasztási szabályokkal	$O (V 3)$	Push-relabel algoritmusvariáns, amely mindig kiválasztja a legutóbb aktív csúcsot, és addig végez push műveleteket, amíg a többlet pozitív vagy a megengedett maradék élek nem jelennek meg ebből a csúcsból.
Push-relabel algoritmus dinamikus fákkal	$O\left(VE\log {\frac {V^{2}}{E}}\right)$	Az algoritmus korlátozott méretű fákat épít a maradék gráfra a magasság függvényében. Ezek a fák többszintű push műveleteket biztosítanak.
KRT (King, Rao, Tarjan) algoritmusa^[11]	$O(EV\log _{\frac {E}{V\log V}}V)$
Bináris blokkoló áramlási algoritmus^[12]	$O\left(E\cdot \min(V^{\frac {2}{3}},{\sqrt {E}})\cdot \log {\frac {V^{2}}{E}}\log {U}\right)$	Az U érték megfelel a hálózat maximális kapacitásának.
James B Orlin + KRT (King, Rao, Tarjan) algoritmusa^[9]	$O(VE)$	Orlin algoritmusa a maximális áramlást $O (VE)$ időben oldja meg $E\leq O(V^{{16 \over 15}-\epsilon })$ míg a KRT $O (VE)$ oldja meg $E>V^{1+\epsilon }$ .

A részletesebb listát lásd:^[13]

Integrált áramlási tétel[szerkesztés]

Az integrált áramlási tétel ezt állítja

Ha az áramlási hálózat minden széle integrált kapacitással rendelkezik, akkor létezik egy integrált maximális áramlás.

Alkalmazás[szerkesztés]

Több forrású, több végpontú maximális áramlási problémája[szerkesztés]

Adott hálózat $N=(V,E)$ egy sor forrással $S=\{s_{1},\ldots ,s_{n}\}$ és egy végpont készlet $T=\{t_{1},\ldots ,t_{m}\}$ csak egy forrás és egy végpont helyett meg kell találnunk a maximális átfolyást $N$ . A több forrású többszörös süllyedési problémát maximális áramlási problémává alakíthatjuk, ha minden egyes csúcshoz csatlakoztatott összevont forrást adunk hozzá $S$ és az egyes csúcsokkal összekötött összevont végpont $T$ (más néven szuperforrás és szupersink) mindkét éle végtelen kapacitással rendelkezik (lásd a 4.1.1. ábrát).

Minimális út fedés az irányított aciklikus gráfban[szerkesztés]

Adott aciklikus gráfot kapunk $G=(V,E)$ , meg kell találnunk az egyes csúcsok lefedéséhez szükséges csúcspontok minimális számát $V$ . Összeállíthatunk kétoldalú gráfot $G'=(V_{out}\cup V_{in},E')$ tól től $G$ , ahol

$V_{out}=\{v\in V:v{\text{ has positive out-degree}}\}$ .
$V_{in}=\{v\in V:v{\text{ has positive in-degree}}\}$ .
$E'=\{(u,v)\in V_{out}\times V_{in}:(u,v)\in E\}$ .

Akkor ezt Kőnig's tételével meg lehet mutatni $G'$ méretének megfelelő $m$ csak akkor, ha léteznek $n-m$ csúcs-diszjunkt útvonalak, amelyek az egyes csúcsokat lefedik $G$ , ahol $n$ a csúcsok száma $G$ . Ezért a problémát úgy lehet megoldani, hogy megtaláljuk a maximális kardinális illesztést $G'$ helyett.

Maximális kardinalitás kétoldalú egyeztetés[szerkesztés]

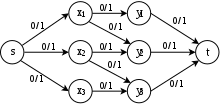
Kétoldalú gráfot kapunk $G=(X\cup Y,E)$ , meg kell találnunk a maximális kardinalitás illesztését $G$ , azaz egyezés, amely a lehető legtöbb élt tartalmazza. Ez a probléma egy hálózat kiépítésével átalakítható maximális áramlási problémává $N=(X\cup Y\cup \{s,t\},E')$ , ahol

$E'$ tartalmazza a széleket $G$ irányítva $X$ nak nek $Y$ .
$(s,x)\in E'$ az egyes $x\in X$ és $(y,t)\in E'$ az egyes $y\in Y$ .
$c(e)=1$ az egyes $e\in E'$ (Lásd a 4.3.1 ábrát).

Ekkor a maximális áramlás értéke $N$ megegyezik a maximális illesztés méretével $G$ .

Maximális áramlás csúcskapacitásokkal[szerkesztés]

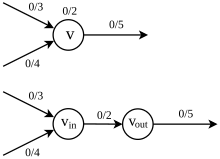
Adott hálózat $N=(V,E)$ , amelyben minden csomóponton van kapacitás az élkapacitáson kívül, azaz egy leképezés $c:V\mapsto \mathbb {R} ^{+}$ , jelölve $c(v)$ , úgy, hogy az áramlás $f$ nemcsak a kapacitáskorlátozásra és az áramlások megőrzésére van szükség, hanem a csúcskapacitási korlátozásra is

\sum _{i\in V}f_{iv}\leq c(v)\qquad \forall v\in V\backslash \{s,t\}

.

Más szavakkal: egy csúcson áthaladó áramlás mennyisége nem haladhatja meg a kapacitását. A maximális átfolyás megtalálása $N$ , kibővítéssel átalakíthatjuk a problémát az eredeti értelemben vett maximális áramlási problémává $N$ . Először is, mindegyik $v\in V$ helyébe a $v_{\text{in}}$ és $v_{\text{out}}$ , ahol $v_{\text{in}}$ össze vannak kötve élekkel $v$ és $v_{\text{out}}$ csatlakozik az élekből származó élekkel $v$ , majd rendeljen kapacitást $c(v)$ az összekötő szélhez $v_{\text{in}}$ és $v_{\text{out}}$ (lásd a 4.4.1. ábrát). Ebben a kibővített hálózatban a csúcskapacitás korlátozása megszűnik, ezért a problémát az eredeti maximális áramlási problémaként lehet kezelni.

Az utak maximális száma s-től t-ig[szerkesztés]

Adott irányított grafikon $G=(V,E)$ és két csúcs $s$ és $t$ , meg kell találnunk a maximális elérési utat $s$ és $t$ -nek. Ennek a problémának több változata van:

1. Az utaknak szélektől elkülönülteknek kell lenniük. Ez a probléma egy hálózat kiépítésével átalakítható maximális áramlási problémává $N=(V,E)$ -től $G$ ,-vel $s$ és $t$ a forrás és a végpont $N$ , és mindegyik élhez kapacitást rendelünk $1$ . Ebben a hálózatban a maximális áramlás $k$ ha vannak $k$ élelválasztó utak.

2. Az útvonalaknak függetleneknek kell lenniük, a csúcsoktól (kivéve: $s$ és $t$ ). Felépíthetünk egy hálózatot $N=(V,E)$ -től $G$ csúcskapacitásokkal, ahol az összes csúcs és az élek kapacitása megegyezik $1$ . Akkor a maximális áramlás értéke megegyezik a független útvonalak maximális számával $s$ nak nek $t$ .

3. Amellett, hogy az útvonalak szélekkel és / vagy csúcsokkal diszjunktívak, az útvonalaknak hossza is korlátozott: csak azokat az útvonalakat vesszük figyelembe, amelyeknek a hossza pontosan megfelel $k$ , de legfeljebb $k$ . A probléma legtöbb változata NP-teljes, kivéve a kis értékű $k$ .^[14]

Bezárási probléma[szerkesztés]

Egy irányított gráf bezárása csúcsok halmaza, kimeneti élek nélkül. Ez azt jelenti, hogy a grafikonnak nem lehetnek olyan szélei, amelyek a bezáráson belül kezdődnek és a bezáráson kívül végződnek. A bezárási probléma az a feladat, hogy megkeressük a maximális vagy minimális tömegű bezárást egy csúcsra súlyozott irányított gráfban. Meg lehet oldani polinomiális időben, a maximális áramlási probléma csökkentésével.

Valós alkalmazások[szerkesztés]

Baseball megszüntetése[szerkesztés]

A baseball kiküszöbölésekor n csapat versenyez egy bajnokságban. Egy bizonyos szakaszában a bajnoki szezonban, w _i a győzelem száma és r _i a játékok száma, i és r _ij a játékban lévő csapatok száma és j a csapat ellen maradt játékok száma. A csapatot kizárják, ha nincs esélye a szezon befejezésére. A baseball kiküszöbölésének problémája annak meghatározása, hogy mely csapatokat távolítsák el a szezon minden pontján. Schwartz^[15] olyan módszert javasolt, amely ezt a problémát a maximális hálózati áramlásig csökkenti. Ebben a módszerben hálózatot hoznak létre annak meghatározására, hogy kiküszöbölésre kerül-e a k csapat.

Legyen G = (V, E) olyan hálózat, ahol s, t ∈ V a forrás és a végpont. Az egyik hozzáad egy játékot csomóponthoz {i, j} ahol i '<j-V,' és összeköti mindegyik S egy él kapacitása r _ij - ami a darabok a két csapat. Minden csoporthoz hozzáadunk egy csomópontot, és minden { i, j } játékcsomópontot összekapcsolunk két i és j csapatcsomóponttal, hogy egyikük nyerjen. Nem szükséges korlátozni az áramlási értéket ezeken a széleken. Végül az i csapat csomópontjától a t süllyedő csomópontig éleket készítünk, és a w _k + r _k - w _i kapacitását úgy állítjuk be, hogy megakadályozzuk az i csapatot abban, hogy w _k + r _k- nál többet nyerjen. Legyen S az összes csapat tagja a bajnokságban, és hagyja $\scriptstyle r(S-\{k\})=\sum _{i,j\in \{S-\{k\}\},i<j}r_{ij}$ . Ebben a módszerben azt állítják, hogy a k csoport nem kerül kiküszöbölésre, ha és csak akkor, ha az r méretű S (S - { k }) áramlási érték létezik a G hálózatban. Az említett cikkben bebizonyosodott, hogy ez az áramlási érték a maximális áramlási érték s- től t-ig.

Légitársaság ütemezése[szerkesztés]

A légiközlekedésben jelentős problémát jelent a repülési személyzet ütemezése. A légitársaságok ütemezési problémáját a kiterjesztett maximális hálózati áramlás alkalmazásának lehet tekinteni. A probléma alapja az F repülések, amelyek információkat tartalmaznak arról, hogy hol és mikor indul és érkezik a repülő. A légitársaságok ütemezésének egyik változatában a cél egy megvalósítható menetrend elkészítése, legfeljebb k legénységgel.

Ennek a problémának a megoldása érdekében a forgalmi probléma egy korlátozott cirkulációnak nevezett változatát alkalmazzák, amely a hálózati áramlási problémák általánosítása, azzal a megkötéssel, hogy az alsó határ a szélső áramlásokon van.

Legyen G = (V, E) olyan hálózat, amelynek s, t ∈ V a forrása és a végpont csomópontjai. Minden i repülés forrásához és rendeltetési helyéhez két csomópontot adunk hozzá V-hez, s _i csomópontot forrásként és d _i csomópontot mint i repülés célcsomópontját. Az egyik a következő éleket egészíti ki az E-vel:

Egy él kapacitása [0, 1] között s és az egyes s _i.
Egy él, amelynek kapacitása [0, 1] az egyes d _i és t között.
Egy él, amelynek kapacitása [1, 1] az s _i és d _i pár között.
Egy él, amelynek kapacitása [0, 1] az egyes d _i és s _{j között}, ha a forrás s _j észszerű idővel és költséggel elérhető az i repülés rendeltetési helyétől.
Egy él, amelynek kapacitása [0, ∞ ] s és t között.

Az említett módszerben azt állítják és bebizonyítják, hogy k áramlási értékének megállapítása G-ben s és t között megegyezik az F repülési készlet megvalósítható ütemtervével, legfeljebb k legénységgel.^[16]

A légitársaságok menetrendjének másik változata a legkevesebb legénység megtalálása az összes járat végrehajtásához. Annak érdekében, hogy megtalálja a választ erre a problémára, egy páros gráf $G' = (A \cup B, E)$ jön létre, ahol minden egyes járat egy példánya másolja A és B értéket. Ha ugyanaz a sík képes végrehajtani a j repülést az i repülés után, akkor i ∈ A csatlakozik a j ∈ B-hez. A $G'$ egyezés indukálja az F ütemtervét, és ebben a grafikonban egyértelműen a maximális kétoldalú egyezés hozza létre a légitársaságok menetrendjét minimális létszámmal.^[16] Amint azt a cikk Alkalmazási részében említik, a kétoldalú maximális kardinális illesztés a maximális áramlási probléma alkalmazása.

Forgalmi és keresleti probléma[szerkesztés]

Vannak olyan gyárak, amelyek árut állítanak elő, és vannak falvak, ahol az árukat át kell szállítani. Ezeket egy úthálózat köti össze, az egyes utak $c$ kapacitással bírnak a rajzon átfolyó maximális áruk számára. A probléma az, hogy kiderüljön, van-e forgalom, amely kielégíti a keresletet. Ez a probléma átalakítható maximális áramlású problémává.

Addott a forrás csomópont $s$ hozzá élek, hogy minden gyárban csomópont $f i$ kapacitása $p i$ ahol $p i$ a termelés mértéke gyári $f i$
Adjunk hozzá egy $t$ süllyedési csomópontot, és adjunk hozzá $v i$ – $t$ összes falutól széleket $d i$ kapacitással, ahol $d i$ a $v i$ falu $v i$ .

Legyen G = (V, E) ez az új hálózat. Létezik egy olyan forgalom, amely csak akkor teljesíti a keresletet:

Maximum flow value(G)

=\sum _{i\in v}d_{i}

.

Ha létezik forgalom, a maximális áramlási megoldás megválaszolása megadja a választ, hogy mennyi árut kell küldeni egy adott úton az igények kielégítéséhez.

A problémát úgy lehet kibővíteni, hogy néhány szélnél az alsó korlátot hozzáfűzzük az áramláshoz.^[17]

Kép szegmentálása[szerkesztés]

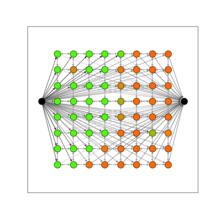
Kleinberg és Tardos^[19] könyvükben algoritmust mutatnak be a kép szegmentálására. Bemutatnak egy algoritmust a kép hátterének és előterének megtalálásához. Pontosabban: az algoritmus bitképként, bemeneti formátumként az alábbiak szerint modellezve: a _i ≥ 0 annak valószínűsége, hogy az i pixel az előtérbe tartozik, b _i ≥ 0 abban a valószínűségben, hogy i pixel a háttérhez tartozik, és p _ij az elágazás, ha két szomszédos i és j képpont az egyik az előtérben, a másik a háttérben helyezkedik el. A cél az, hogy megtalálja a pixelek halmazát (A, B), amely maximalizálja a következő mennyiséget

$q(A,B)=\sum _{i\in A}a_{i}+\sum _{i\in B}b_{i}-\sum _{i,j{\text{adjacent with }}|A\cap \{i,j\}|=1}p_{ij}$ ,

Valóban, minden A pixelben (előtérnek tekintve), a _{i-t kapunk,} minden B pixelben (háttérnek tekintve) b _{i-t kapunk}. A határon, két szomszédos i és j képpont között, p _{ij-t veszít}. Ez megegyezik a mennyiség minimalizálásával

$q'(A,B)=\sum _{i\in A}b_{i}+\sum _{i\in B}a_{i}+\sum _{i,j{\text{adjacent with }}|A\cap \{i,j\}|=1}p_{ij}$

mivel $q(A,B)=\sum _{i}a_{i}+\sum _{i}b_{i}-q'(A,B)$ .

Most azt a hálózatot építjük fel, amelynek csomópontjai a pixel, valamint egy forrás és egy végpont, lásd a jobb oldali ábrát. Mi csatlakozni a forrás pixel i egy él súlya a _i. Az i pixelt és a végpontot b _i tömeg szélével kötik össze. Az i pixelt és a j i pixelt összekötjük p _ij tömeggel. Most meg kell számolnia egy minimális vágást ebben a hálózatban (vagy ezzel egyenértékűen a maximális áramlást). Az utolsó ábra a minimális vágást mutatja.

Bővítmények[szerkesztés]

1. A mimimum-cost flow problémájánál az egyes éleknek (u, v) kapacitásukon felül egy _uv költség-együttható is van. Ha a szélén átfolyó áram f _uv, akkor a teljes költség _uv f _uv. Meg kell találni egy adott d méretű áramlást a legkisebb költséggel. A legtöbb változatban a költség-együtthatók pozitív vagy negatív lehetnek. Különböző polinomiális idő algoritmusok léteznek erre a problémára.

2. A maximális áramlási problémát diszjunktív korlátozásokkal egészíthetjük ki: egy negatív diszjunktív kényszer azt mondja, hogy egy bizonyos élpárnak nem lehet egyszerre nem nulla áramlása; egy pozitív diszjunktív kényszer azt mondja, hogy egy bizonyos élpárban legalább egyiknek nem lehet nulla áramlással rendelkeznie. Negatív korlátozások esetén a probléma az egyszerű hálózatoknál is strongly NP-hard-á válik. Pozitív korlátozások esetén a probléma polinomiális, ha frakcionált áramlások megengedettek, de strongly NP-hard lehet, ha az áramlásoknak integráltaknak kell lenniük.^[20]

Jegyzetek[szerkesztés]

↑ ^a ^b ^c Schrijver (2002). „On the history of the transportation and maximum flow problems”. Mathematical Programming 91 (3), 437–445. o. DOI:10.1007/s101070100259.
↑ Gass, Saul I.. Mathematical, algorithmic and professional developments of operations research from 1951 to 1956, An Annotated Timeline of Operations Research, International Series in Operations Research & Management Science, 79–110. o.. DOI: 10.1007/0-387-25837-X_5 (2005). ISBN 978-1-4020-8116-3
↑ ^a ^b Harris (1955). „Fundamentals of a Method for Evaluating Rail Net Capacities”. Research Memorandum. [2017. február 17-i dátummal az eredetiből archiválva]. (Hozzáférés: 2020. május 20.)
↑ Ford (1956). „Maximal flow through a network”. Canadian Journal of Mathematics 8, 399–404. o. DOI:10.4153/CJM-1956-045-5.
↑ ^a ^b Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
↑ Sherman, Jonah. Nearly Maximum Flows in Nearly Linear Time, Proceedings of the 54th Annual IEEE Symposium on Foundations of Computer Science, 263–269. o.. DOI: 10.1109/FOCS.2013.36 (2013). ISBN 978-0-7695-5135-7
↑ Kelner, J. A.. An Almost-Linear-Time Algorithm for Approximate Max Flow in Undirected Graphs, and its Multicommodity Generalizations, Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, 217. o.. DOI: 10.1137/1.9781611973402.16 (2014). ISBN 978-1-61197-338-9
↑ Knight: New algorithm can dramatically streamline solutions to the 'max flow' problem. MIT News, 2014. január 7. [2014. február 26-i dátummal az eredetiből archiválva]. (Hozzáférés: 2014. január 8.)
↑ ^a ^b Orlin, James B.. Max flows in O(nm) time, or better, 765–774. o.. DOI: 10.1145/2488608.2488705 (2013). ISBN 9781450320290
↑ Malhotra (1978). „An $O(|V|^{3})$ algorithm for finding maximum flows in networks”. Information Processing Letters 7 (6), 277–278. o. DOI:10.1016/0020-0190(78)90016-9.
↑ King (1994). „A Faster Deterministic Maximum Flow Algorithm”. Journal of Algorithms 17 (3), 447–474. o. DOI:10.1006/jagm.1994.1044.
↑ Goldberg (1998). „Beyond the flow decomposition barrier”. Journal of the ACM 45 (5), 783. o. DOI:10.1145/290179.290181.
↑ Goldberg (1988). „A new approach to the maximum-flow problem”. Journal of the ACM 35 (4), 921. o. DOI:10.1145/48014.61051.
↑ Itai (1982. április 25.). „The complexity of finding maximum disjoint paths with length constraints” (angol nyelven). Networks 12 (3), 277–286. o. DOI:10.1002/net.3230120306. ISSN 1097-0037.
↑ Schwartz (1966). „Possible Winners in Partially Completed Tournaments”. SIAM Review 8 (3), 302–308. o. DOI:10.1137/1008062.
↑ ^a ^b Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. 26. Maximum Flow, Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 643–668. o. (2001). ISBN 978-0-262-03293-3
↑ Carl Kingsford: Max-flow extensions: circulations with demands
↑ Project imagesegmentationwithmaxflow, that contains the source code to produce these illustrations. (angol nyelven). GitLab. (Hozzáférés: 2019. december 22.)
↑ Algorithm Design (angol nyelven). www.pearson.com. (Hozzáférés: 2019. december 21.)
↑ Schauer (2013. július 1.). „The maximum flow problem with disjunctive constraints” (angol nyelven). Journal of Combinatorial Optimization 26 (1), 109–119. o. DOI:10.1007/s10878-011-9438-7. ISSN 1382-6905.

Fordítás[szerkesztés]

Ez a szócikk részben vagy egészben a Maximum flow problem című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

További információk[szerkesztés]

Joseph Cheriyan and Kurt Mehlhorn (1999). „An analysis of the highest-level selection rule in the preflow-push max-flow algorithm”. Information Processing Letters 69 (5), 239–242. o. DOI:10.1016/S0020-0190(99)00019-8.
Daniel D. Sleator and Robert E. Tarjan (1983). „A data structure for dynamic trees”. Journal of Computer and System Sciences 26 (3), 362–391. o. DOI:10.1016/0022-0000(83)90006-5. ISSN 0022-0000.
Eugene Lawler. 4. Network Flows, Combinatorial Optimization: Networks and Matroids. Dover, 109–177. o. (2001). ISBN 978-0-486-41453-9

[:0-1] Schrijver (2002). „On the history of the transportation and maximum flow problems”. Mathematical Programming 91 (3), 437–445. o. DOI:10.1007/s101070100259.

[2] Gass, Saul I.. Mathematical, algorithmic and professional developments of operations research from 1951 to 1956, An Annotated Timeline of Operations Research, International Series in Operations Research & Management Science, 79–110. o.. DOI: 10.1007/0-387-25837-X_5 (2005). ISBN 978-1-4020-8116-3

[:2-3] Harris (1955). „Fundamentals of a Method for Evaluating Rail Net Capacities”. Research Memorandum. [2017. február 17-i dátummal az eredetiből archiválva]. (Hozzáférés: 2020. május 20.)

[:1-4] Ford (1956). „Maximal flow through a network”. Canadian Journal of Mathematics 8, 399–404. o. DOI:10.4153/CJM-1956-045-5.

[:3-5] Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).

[6] Sherman, Jonah. Nearly Maximum Flows in Nearly Linear Time, Proceedings of the 54th Annual IEEE Symposium on Foundations of Computer Science, 263–269. o.. DOI: 10.1109/FOCS.2013.36 (2013). ISBN 978-0-7695-5135-7

[7] Kelner, J. A.. An Almost-Linear-Time Algorithm for Approximate Max Flow in Undirected Graphs, and its Multicommodity Generalizations, Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, 217. o.. DOI: 10.1137/1.9781611973402.16 (2014). ISBN 978-1-61197-338-9

[8] Knight: New algorithm can dramatically streamline solutions to the 'max flow' problem. MIT News, 2014. január 7. [2014. február 26-i dátummal az eredetiből archiválva]. (Hozzáférés: 2014. január 8.)

[orlin-9] Orlin, James B.. Max flows in O(nm) time, or better, 765–774. o.. DOI: 10.1145/2488608.2488705 (2013). ISBN 9781450320290

[10] Malhotra (1978). „An $O(|V|^{3})$ algorithm for finding maximum flows in networks”. Information Processing Letters 7 (6), 277–278. o. DOI:10.1016/0020-0190(78)90016-9.

[11] King (1994). „A Faster Deterministic Maximum Flow Algorithm”. Journal of Algorithms 17 (3), 447–474. o. DOI:10.1006/jagm.1994.1044.

[12] Goldberg (1998). „Beyond the flow decomposition barrier”. Journal of the ACM 45 (5), 783. o. DOI:10.1145/290179.290181.

[13] Goldberg (1988). „A new approach to the maximum-flow problem”. Journal of the ACM 35 (4), 921. o. DOI:10.1145/48014.61051.

[14] Itai (1982. április 25.). „The complexity of finding maximum disjoint paths with length constraints” (angol nyelven). Networks 12 (3), 277–286. o. DOI:10.1002/net.3230120306. ISSN 1097-0037.

[15] Schwartz (1966). „Possible Winners in Partially Completed Tournaments”. SIAM Review 8 (3), 302–308. o. DOI:10.1137/1008062.

[ITA-16] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. 26. Maximum Flow, Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 643–668. o. (2001). ISBN 978-0-262-03293-3

[17] Carl Kingsford: Max-flow extensions: circulations with demands

[18] Project imagesegmentationwithmaxflow, that contains the source code to produce these illustrations. (angol nyelven). GitLab. (Hozzáférés: 2019. december 22.)

[19] Algorithm Design (angol nyelven). www.pearson.com. (Hozzáférés: 2019. december 21.)

[20] Schauer (2013. július 1.). „The maximum flow problem with disjunctive constraints” (angol nyelven). Journal of Combinatorial Optimization 26 (1), 109–119. o. DOI:10.1007/s10878-011-9438-7. ISSN 1382-6905.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]