Andrásfai-gráf

Andrásfai-gráf
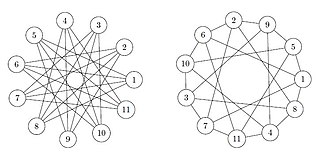n=4-re (kétféle rajzolatban)
Névadó	Andrásfai Béla
Csúcsok száma	3n-1
Élek száma	n(3n-1)/2
Átmérő	2
Kromatikus szám	n
Egyéb	reguláris
Jelölés	$And(n)$

Az Andrásfai-gráf olyan 3n-1 csúcsú gráf, amely nem tartalmaz sem háromszöget, sem n+1 független csúcsot. Nevét onnan kapta, hogy Andrásfai Béla írta le először.

Értelmezése és tulajdonságai

Az Andrásfai-gráf minden tetszőleges $n\geq 1$ természetes számra olyan $3n-1$ csúcsú gráf, amelyben az $i$ csúcsot $(1\leq i\leq 3n-1)$ él köti össze az $(i+j-1)\!\!\!\mod (3n-1)+1$ csúcsokkal, minden $j=n,n+1,...,2n-1$ értékre. Az ilyen gráf jelölése: $And(n)$.

A gráf jellemzője, hogy nem tartalmaz sem háromszöget (azaz $K_{3}$-at), sem $n+1$ független csúcsot (azaz a komplementere nem tartalmaz $K_{n+1}$-et). Ebből következik, hogy az $R(3,n)$ Ramsey-számra fennáll, hogy $R(3,n)\geq 3(n-1).$ Egyenlőség csak $n=3$ és $n=4$ értékekre áll fenn.

A gráfot úgy is lehet értelmezni, hogy a csúcsokat egyenlően elosztjuk egy képzeletbeli körön, minden csúcsból kiindulva berajzoljuk képzeletben a szabályos körbeírható háromszöget, majd az illető csúcsot összekötjük a háromszög szemben levő oldalához tartozó köríven levő csúcsokkal. (lásd az ábra első rajzolatát). Gyakorlatilag ez azt jelenti, hogy egy adott csúcstól balra és jobbra kihagyunk $n-1$ csúcsot, majd a többivel összekötjük.

Az Andrásfai-gráfokat később általánosították két irányba is.

Az első hat Andrásfai-gráf

LaTeX program Andrásfai-gráf rajzolására:

\documentclass{article}
\usepackage{tikz}
\textwidth=15cm

\newcommand{\Andr}[3]{
 % #1 n
 % #2 elfordítási szög fokban
 % #3 \draw vagy \fill (a csúcs kis kör vagy korong)
 \begin{tikzpicture}[rotate=#2,scale=2]
  \pgfmathsetmacro{\n}{3*#1 - 1};     % \n értéke 3n-1
  \pgfmathsetmacro{\m}{2*#1 - 1};     % \m értéke 2n-1
  \foreach \i in {1,...,\n}
  {
    \path (360/\n*\i:1cm) node (X\i) { }; % csúcsok egyenletes elosztása a körön
    #3 (X\i) circle (2pt);                % csúcsok rajzolása
  }
   \foreach \i in {1,...,\n}
  {
   \foreach \j in {#1,...,\m}
    {   \pgfmathtruncatemacro{\p}{1+ mod(\i+\j-1,\n)}; % i-vel összekötendő csúcs kiszámítása
        \draw (X\i) -- (X\p);                          % élek rajzolása
    }
  }
 \end{tikzpicture}
}

\begin{document}
\centering
   \Andr{1}{0}{\fill}\quad
   \Andr{2}{90}{\fill}\quad
   \Andr{3}{0}{\draw[fill=blue]}
      
\bigskip
\hspace*{2cm} n=1 \hfill n=2 \hfill n=3 \hspace*{2cm}
   
\bigskip
   \Andr{4}{0}{\draw[fill=blue]}\quad
   \Andr{5}{0}{\draw[fill=red]}\quad
   \Andr{6}{0}{\draw[red]}

\bigskip
\hspace*{2cm} n=4 \hfill n=5 \hfill n=6 \hspace*{2cm}

\bigskip
   \Andr{7}{0}{\draw[fill=green]}\quad
   \Andr{8}{0}{\draw[magenta]}\quad
   \Andr{9}{0}{\draw[fill=gray]}

\bigskip
\hspace*{2cm} n=7 \hfill n=8 \hfill n=9 \hspace*{2cm}

\end{document}

Források

• Godsil, C., Royle, G.: Algebraic Graph Theory, Springer-Verlag, New York, pp. 118-123, 2001. (§6.10-6.12: The Andrásfai Graphs, Colouring Andrásfai Graphs, A Characterization)
• Andrásfai Béla: Ismerkedés a gráfelmélettel, Tankönyvkiadó, Budapest, 1971. pp. 132-135.
• Weisstein, Eric W.: Andrásfai Graph (angol nyelven). Wolfram MathWorld

Kapcsolódó szócikkek

• Ramsey-tétel
• Petersen-gráf
• Cayley-gráf