Norton-tétel
Norton-tétel szerint bármely, generátorokból és ellenállásokból álló kétpólus[1] helyettesíthető egy áramgenerátorral, és a vele párhuzamosan kapcsolt belső ellenállással. A tétel nemcsak ellenállásokra, hanem egyetlen frekvenciát tartalmazó váltakozó áramú rendszerek esetén impedanciákra is alkalmazható. A Norton helyettesítő áramkör bármely, lineáris forrásokból és impedanciákból álló hálózatot leír, valamely adott frekvencián. Az áramkör egy ideális áramgenerátorból és a vele párhuzamosan kapcsolt ideális impedanciából (vagy nem reaktív áramkörök esetén ellenállásból) áll.
Norton tétele a Thévenin-tétel kiegészítése, melyet 1926-ban egymástól függetlenül ketten is leírtak, a Hause-Siemens kutatója, Hans Ferdinand Mayer és a Bell Laboratories mérnöke, Edward Lawry Norton. Valójában Mayer volt az, aki kettőjük közül a tételt publikálta, de Norton a Bell Laboratories belső műszaki értesítőjén keresztül ismertette a tételt.

A Norton helyettesítő kapcsolás számítása[szerkesztés]
A Norton helyettesítő áramkör egy INo áramgenerátorból és a vele párhuzamosan kapcsolt RNo ellenállásból áll. A helyettesítő kapcsolás kiszámításához
- Határozzuk meg az INo Norton-áramot. Számítsuk ki az IAB kimeneti áramot abban az esetben, ha a terhelést rövidzárral helyettesítjük (vagyis A és B közötti ellenállás 0). Ez az áram: INo.
- Határozzuk meg az RNo Norton-ellenállást. Abban az esetben, ha nincsenek egymástól függő források (vagyis az összes feszültséggenerátor és áramgenerátor független), az RNo Norton-impedancia a következőképpen határozható meg:
- Számítsuk ki a VAB kimeneti feszültséget nyitott áramkör esetében (vagyis mikor az áramkör terhelő ellenállása végtelen). Ekkor RNo megegyezik VAB és INo hányadosával.
- vagy
- Helyettesítsük a független feszültséggenerátorokat rövidzárakkal és a független áramgenerátorokat szakadással. A kimeneti kapcsokon mérhető teljes ellenállás az RNo Norton-impedancia.
- Ha azonban az áramkörben nemcsak független források vannak, akkor az általánosabb módszert kell alkalmazni.
- Kapcsoljunk egy 1 A-es állandó áramot adó áramgenerátort az áramkör kimeneti kapcsaira, és számítsuk ki a kapcsain létrejövő feszültséget. Ennek a feszültségnek és az 1 A-es áramnak a hányadosa lesz az RNo Norton-impedancia. Ezt a módszert kell alkalmazni, ha az áramkör nem független forrásokat is tartalmaz, de akkor is használható a módszer, ha az áramkörben csak független források vannak.
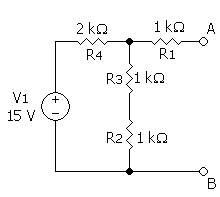
Példa a Norton helyettesítő áramkörre[szerkesztés]
 |
 |
 |

A példában az Iteljes teljes áramot a következő képlet adja meg:
A terhelésen átfolyó áram, az áramosztás szabálya szerint:
A kívülről látható helyettesítő ellenállás:
Így a helyettesítő áramkör egy 3,75 mA-es áramgenerátor egy 2 kΩ-os ellenállással párhuzamosan kötve.
Átalakítás Thévenin-féle helyettesítő áramkörré[szerkesztés]
A Norton helyettesítő áramkörnek a Thévenin helyettesítő áramkörrel való kapcsolatát a következő egyenletek írják le:
Lásd még[szerkesztés]
Források[szerkesztés]
- BME: Thévenin- és Norton-tételek[halott link]
- Origins of the equivalent circuit concept
- Norton's theorem at allaboutcircuits.com
Jegyzetek[szerkesztés]
- ↑ Olyan áramkör, amelynek két kivezetése, csatlakozási pontja van.







