Lejtő
A lejtő egy teher felemeléshez szükséges erő csökkentésére szolgáló egyszerű gép. A lejtő a vízszintessel kis szöget bezáró sík, melyre sokkal könnyebb felvontatni egy nehéz tárgyat, mint függőlegesen felemelni. A kisebb erőszükséglet „ára”, hogy a vontatás hossza arányosan megnő, így fizikai értelemben munkát megtakarítani segítségével nem lehet, viszont a kisebb erőszükséglet miatt könnyebb végrehajtani. A lejtő elvére vezethető vissza az ék és a csavar is.
Súrlódás nélküli eset[szerkesztés]

Az idealizált, súrlódás nélküli esetre egy lejtőn a testre ható erők egyensúlyát a mellékelt ábra mutatja. A test súlya két összetevőre bontható: a lejtővel párhuzamos erőre és a lejtőre merőleges erőre. Ezekre a következő összefüggések írhatók fel:
Ebben az esetben az áttétel (erőnyereség):
- ,
vagyis ennyiszer kisebb erő szükséges a lejtőn való felvontatásához (ha a vontató erő párhuzamos a lejtővel), mint a teher súlya.
Amennyiben nincs vontatóerő, a súly lejtő irányú komponense gyorsulással fogja gyorsítani az tömegű testet, és írható:
és innen a lejtő menti gyorsulás:
Súrlódásos eset[szerkesztés]
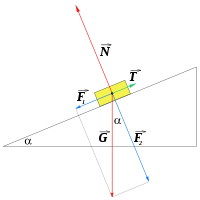
Súrlódás esetén az erők hasonlóak. Itt azonban két esetet kell megkülönböztetni. Ha a teher nyugalomban van, a súlyerő lejtő irányú komponense éppen egyenlő a súrlódással. A súrlódási erő legnagyobb értéke súrlódási tényező esetén
Innen
vagyis annak feltétele, hogy egy lejtőn ne csússzon le egy test, az a feltétele, hogy a súrlódási tényezőnél kisebb legyen a lejtő hajlásszögének tangense. Ha bevezetjük a súrlódás kúpszögét:
akkor az egyensúly feltétele így is írható:
Ha az egyensúly nem áll fenn, és a súrlódás kisebb, mint a lejtő hajlásszögének tangense, akkor a test egyenletes gyorsulással elindul a lejtőn lefelé. A gyorsulás értékének meghatározásához ismét az erőkomponenseket kell megvizsgálni. A súrlódási erő mindig a mozgással ellentétes irányú, így a lejtő irányába ható erők egyensúlya:
Ebből az gyorsulás értéke:
Története[szerkesztés]
A lejtő az emberiség által legrégebben használt gépek egyike, feltalálása messze a történelem előtti időkbe nyúlik vissza. A megalitok felállításánál kellett, hogy használják, de a piramisok építésénél is felhasználták.
A 17. században Galilei használta a lejtőn legurított golyók vizsgálatára, ennek alapján fogalmazta meg híres tételét, hogy a szabadon eső testek mozgása nem függ a test tömegétől. Ez ellentmondott az akkoriban általánosan elismert arisztotelészi véleménnyel, hogy egy test annál gyorsabban esik, minél súlyosabb. Lejtős kísérletei vezettek annak felismerésére, hogy az egyenletesen gyorsuló mozgás során megtett út az eltelt idő négyzetével arányos.




















