Konfliktusvezérelt klóztanulás

Az informatikában a konfliktusvezérelt klóztanulás (CDCL) a logikai kielégítési probléma (SAT) megoldására szolgáló algoritmus. Adott egy logikai képlet, a SAT-probléma változók hozzárendelését kéri, hogy a teljes képlet igaz legyen. A CDCL SAT megoldók belső működését a DPLL megoldók ihlették. A fő különbség a CDCL és a DPLL között az, hogy a CDCL visszaugrása nem kronologikus.

A konfliktusvezérelt klózok tanulását Marques-Silva és Sakallah (1996, 1999), valamint Bayardo és Schrag (1997) javasolta.

Háttér

Logikai kielégítési probléma

A kielégítési probléma abban áll, hogy egy adott képlethez megfelelő hozzárendelést találunk konjunktív normál formában (CNF).

( ( nem A ) vagy ( nem C ) ) és ( B vagy C ),

vagy egy általános jelöléssel:

$(\lnot A\lor \lnot C)\land (B\lor C)$

ahol A, B, C logikai változók, $\lnot A$, $\lnot C$, $B$, és $C$ litárlok, és $\lnot A\lor \lnot C$ és $B\lor C$ klózok.

$A=\mathrm {False} ,B=\mathrm {False} ,C=\mathrm {True}$

mivel igazzá teszi az első klózt (hiszen $\lnot A$ igaz), valamint a másodikat (mivel $C$ igaz).

Ez a példa három változót használ ( A, B, C ), és mindegyikhez két lehetséges hozzárendelés (igaz és hamis) van. Tehát az egyiknek van $2^{3}=8$ lehetősége. Ebben a kis példában a brute-force keresést használhatjuk az összes lehetséges hozzárendelés kipróbálásához, és ellenőrizhetjük, hogy megfelelnek-e a képletnek.

De realisztikus alkalmazásokban, amelyekben milliónyi változó és klóz található, a brute force keresés nem praktikus. A SAT-megoldó feladata, hogy hatékonyan és gyorsan megtalálja a kielégítő feladatot összetett CNF-képletek különböző heurisztikáinak alkalmazásával.

Unit klóz szabály (unit propagáció vagy egységterjesztés)

Ha egy nem kielégítő klóznak egy kivételével minden literálja vagy változója Hamis értékkel van kiértékelve, akkor a szabad literálnak igaznak kell lennie ahhoz, hogy a klóz igaz legyen. Például, ha az alábbi nem kielégítő klózt a következővel értékeljük ki $A=\mathrm {Hamis}$ és $B=\mathrm {Hamis}$ nekünk kell hogy legyen $C=\mathrm {Igaz}$ a klóz érdekében $(A\lor B\lor C)$ hogy igaz legyen.

A unit klóz szabály iterált alkalmazását unit propagációnak vagy Boole-kényszer-propagációnak (BCP) nevezik.

Rezolúció

Vegyünk két kitételt $(A\lor B\lor C)$ és $(\neg C\lor D\lor \neg E)$. A klóz $(A\lor B\lor D\lor \neg E)$, amelyet a két klóz egyesítésével és mindkettő eltávolításával kapunk $\neg C$ és $C$, a két klóz oldójának nevezzük.

Algoritmus

A konfliktus-vezérelt klózok tanulása a következőképpen működik.

1. Válasszon ki egy változót, és rendelje hozzá az igaz vagy hamis értéket. Ezt döntési állapotnak nevezik. Emlékezzen a feladatra.
2. Alkalmazza a logikai kényszer propagációt (unit propagáció).
3. Építsd meg az implikációs gráfot.
4. Ha bármilyen konfliktus van
   1. Keresse meg az implikációs grafikonon azt a vágást, amely az ütközéshez vezetett
   2. Hozz létre egy új klózt, amely a konfliktushoz vezető hozzárendelések tagadása
   3. Nem kronologikusan visszalépni ("visszaugrás") a megfelelő döntési szintre, ahol az elsőként hozzárendelt, a konfliktusban érintett változót hozzárendelték
5. Ellenkező esetben folytassa az 1. lépéstől, amíg az összes változóértéket hozzá nem rendeli.

Példa

A CDCL algoritmus vizuális példája:

• 
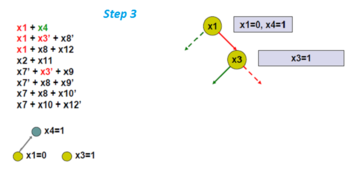
  Első elágazó változónál válasszuk az x1-et. A sárga kör tetszőleges döntést jelent.
• 
  Most alkalmazza a unit propagációt, ami azt eredményezi, hogy x4-nek 1-nek kell lennie (azaz igaznak). A szürke kör a unit propagáció során kényszerített változó hozzárendelést jelent. Az így kapott gráfot implikációs gráfnak nevezzük.
• 
  Tetszőlegesen válasszon másik elágazó változót, az x3-at.
• 
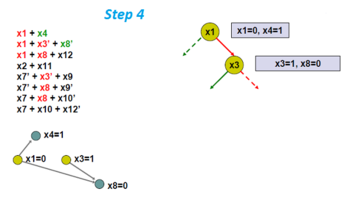
  Alkalmazza a unit propagációt, és keresse meg az új implikációs gráfot.
• 
  Itt az x8 és x12 változók 0-ra, illetve 1-re vannak kényszerítve.
• 
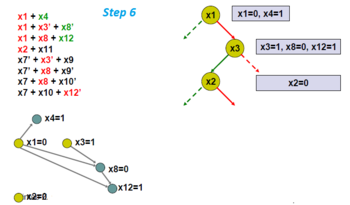
  Válasszon egy másik elágazó változót, x2.
• 
  Keresse meg az implikációs gráfot.
• 
  Válasszon egy másik elágazási változót, az x7-et.
• 
  Keresse meg az implikációs gráfot.
• 
  Talált konfliktust!
• 
  Keresse meg azt a vágást, amely ehhez a konfliktushoz vezetett. A vágásból keressen egy ellentétes állapotot.
• 
  Vegyük ennek a feltételnek a tagadását, és tegyük klózzá.
• 
  Konfliktus klóz hozzáadása a problémához.
• 
  Nem időrendi backtrack a megfelelő döntési szintre, amely ebben az esetben a tanult klóz literáljainak második legmagasabb döntési szintje.
• 
  Visszaugrás és változó értékek beállítása ennek megfelelően.

Teljesség

A DPLL egy megbízható és teljes algoritmus a SAT számára. A CDCL SAT megoldói megvalósítják a DPLL-t, de megtanulhatnak új klózokat, és nem kronologikusan léphetnek vissza. A konfliktuselemzéssel végzett klóztanulás nem befolyásolja sem a megalapozottságot, sem a teljességet. Az új klózokat feloldási művelettel azonosítja az ütközéselemzés. ezért minden egyes tanult klóz kikövetkeztethető az eredeti klózból és a többi tanult klózból a feloldási szekvencia sorozatával. Ha cN az új tanult klóz, akkor ϕ akkor és csak akkor teljesíthető, ha ϕ ∪ {cN} is kielégíthető. Ezen túlmenően a módosított backtrack lépés sem befolyásolja a megbízhatóságot vagy a teljességet, mivel a visszalépési információkat minden új tanult klózból kapjuk.

Alkalmazások

A CDCL algoritmus fő alkalmazása a különböző SAT-megoldókban található, beleértve:

• MiniSAT
• Zchaff SAT
• Z3
• Glükóz
• ManySAT stb.

A CDCL algoritmus annyira erőssé tette a SAT-megoldókat, hogy számos alkalmazási területen alkalmazzák hatékonyan a gyakorlatban, mint például a mesterséges intelligencia tervezése, bioinformatika, szoftverteszt-minta generálása, szoftvercsomag-függőségek, hardver- és szoftvermodell-ellenőrzés és kriptográfia.

Kapcsolódó algoritmusok

A CDCL-hez kapcsolódó algoritmusok a Davis–Putnam-algoritmus és a DPLL algoritmus. A DP algoritmus rezolúció cáfolatokat használ, és lehetséges memóriaelérési problémája van. Míg a DPLL algoritmus megfelelő a véletlenszerűen generált példányokhoz, rossz a gyakorlati alkalmazásokban generált példányokhoz. A CDCL hatékonyabb megoldás az ilyen problémák megoldására, mivel a CDCL alkalmazása kevesebb állapottér-keresést biztosít a DPLL-hez képest.

• 
  DPLL: nincs tanulás és időrendi visszalépés (backtrack).
• 
  CDCL: konfliktus-vezérelt záradéktanulás és nem – kronologikus visszalépés.

Fordítás

Ez a szócikk részben vagy egészben a Conflict-driven clause learning című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Források

• Martin Davis (1960). „A Computing Procedure for Quantification Theory”. J. ACM 7, 201–215. o. DOI:10.1145/321033.321034.  
• Martin Davis (1962. július 1.). „A machine program for theorem-proving”. Communications of the ACM 5, 394–397. o. DOI:10.1145/368273.368557.  
• Matthew W. Moskewicz. Chaff: engineering an efficient SAT solver, Proc. 38th Ann. Design Automation Conference (DAC), 530–535. o. (2001) 
• Lintao Zhang. Efficient conflict driven learning in a boolean satisfiability solver, Proc. IEEE/ACM Int. Conf. on Computer-aided design (ICCAD), 279–285. o. (2001) 
• Presentation – "SAT-Solving: From Davis-Putnam to Zchaff and Beyond" by Lintao Zhang. (Several pictures are taken from his presentation)