Klaszteranalízis
A klaszteranalízis egy olyan dimenziócsökkentő eljárás, amellyel adattömböket tudunk homogén csoportokba sorolni, klasszifikálni. Ezeket a csoportokat nevezzük klasztereknek. Az egyes klasztereken belüli adatok valamilyen dimenzió szerint hasonlítanak egymáshoz, és e dimenzió mentén különböznek a többi klaszter elemeitől. A csoportok minél homogénebbek (azaz nagyobb az elemeik hasonlósága), és minél nagyobb közöttük a különbség, annál pontosabbnak mondható a klaszteranalízis maga. A csoportosítás alapját különböző távolság- vagy hasonlóságmértékek képezik.
Mivel az adatok értelmes szétválasztása, csoportba sorolása fontos célja számos tudomány-, üzleti- és informatikai területnek, azért a klaszteranalízis gyakran használt megoldása az adatbányászatnak, a minta felismerésnek, a képelemzésnek, az információ előhívásnak, a bioinformatikának, az adattömörítésnek és a számítógépes grafikának.
A klaszteranalízis nem egy bizonyos konkrét eljárás, hanem egy csoportosító megoldás ami az eredeti adatokat értelmes vagy hasznos csoportokra (klaszterekre) bontja – a kívánt végcéltől függően. (Fülöp, 2006) Ennek megfelelően a klaszterek kialakítására számos különböző, a klaszter fogalmát egymástól jelentősen eltérően definiáló eljárás használható. A népszerű klaszterelképzelések közé tartoznak az egymástól kis távolságra levő csoporttagokat tartalmazó klaszterek, a sűrűbben elhelyezkedő adatok halmazait bekerítő területek, szakaszok vagy bizonyos meghatározott statisztikai eloszlások. Így a klaszterezés többcélú optimizálási problémává tud válni. Az, hogy mi a megfelelő klaszterezési algoritmus és hogy milyen paramétereket javasolt használni (ide értve például a távolság funkciót, a sűrűségi határértéket, vagy azt, hogy mi az elvárt klaszter szám), attól függ, hogy mi az elérni kívánt szándék a klaszterezési eljárással. A klaszteranalízis nem egy automatizált feladat, hanem ismétlődő tudás kinyerésére irányuló vagy próbákat és kudarcokat is tartalmazó, interaktív optimalizáció folyamat. Az alkalmazása alatt gyakran szükséges, hogy módosítva legyenek az adatok és a modell paraméterek egészen addig, amíg az eredmény a kívánt tulajdonságokat tükrözi. A lentebbi ábrán látható, az adatok egy tipikus halmaza – ezek különböző klaszterezési eljárásokkal különböző klaszterekbe sorolhatól, az eljárás előtt így fontos definiálni, hogy mi a célunk, mi a klaszter pontos fogalma számunkra.
A klaszterezés kifejezésen kívül még gyakran használt kifejezés erre az eljárásra az automatizált osztályozás, numerikus taxonómia és tipológiai analízis.
A klaszteranalízis megszületése Driver és Kroeber (1932) nevéhez köthető, míg pszichológiában ismertté Cattel (1943) tette a vonáselméleti klasszifikáció alkalmazása során.
Fogalom[szerkesztés]
Azért is van annyi féle klaszterezési algoritmus, mivel a klaszter fogalmát nehéz precízen definiálni, azonban mindegyikben megtalálható egy közös nevező: az adatcsoportosítási cél csak az adatok tulajdonságai alapján. Az, hogy megértsük a különböző klasztermodellek alapelvét, elengedhetetlen ahhoz, hogy megértsük a különböző klaszterező algoritmusok közötti különbségeket.
Tipikus modellek közé tartoznak például (Fülöp, 2006 nyomán) :
- Kapcsolódási (jól elkülönítő) modellek: távolsági kapcsolatokon alapuló modellek, amikben minden pont közelebb van minden, a pont klaszterében található ponthoz, mint bármely más klaszterben található más ponthoz
- Centroid (középpont alapú) modellek: minden klaszter egy átlagvektor alapján reprezentált; ezeknél a klasztereknél a klaszter prototípusa folytonos adatoknál a klaszter összes pontjának átlaga, míg kategorikus tulajdonságokkal is jellemző pontoknál azok mediodja, azaz legjellemzőbb pontja (jellemző algoritmus: megpróbálja megkeresni a felhasználó által megadott számú (K) klasztert, amelyeket a középpontjaik képviselnek)
- Gráf (szomszédság alapú) modellek: minden pont közelebb van legalább egy, a pont klaszterében található ponthoz, mint bármely más klaszterben található más ponthoz; ez a klaszterdefiníció akkor hasznos, amikor zajosak az adatok, összefonódók a klaszterek. (Jellemző algoritmus: hierarchikus klaszterezés: kezdetben minden elem egy külön klaszterbe tartozik, és ezután minden lépésben a két legközelebbi klaszter kerül összevonásra egészen addig, amíg már csak egyetlen, minden elemet magába foglaló klaszter nem marad)
- Disztribúciós modellek: a klaszterek statisztikai eloszlásokat modelleznek (például többváltozós normál eloszlás)
- Sűrűségen alapuló modellek: itt a klaszterek olyan sűrű tartományai az adathalmaznak, amit egy kevésbé sűrű terület vesz körül (jellemző algoritmus: DBSCAN felosztó klaszterezést hajt végre, a klaszterek számát az algoritmus automatikusan határozza meg. Az alacsony sűrűségű tartományokba eső pontokat az eljárás zajként osztályozza és kihagyja, így nem generál teljes klaszterezést)
A klaszterezés szintén megkülönböztethető az alapján, hogy mennyire éles a klaszterek közötti választóvonal:
- Kemény klaszterezés: minden elem egy bizonyos klaszterbe tartozik vagy nem tartozik bele
- Puha (fuzzy) klaszterezés: minden elem része valamilyen mértékben egy klaszternek; minden elem kap egy tagsági súlyt, melynek értéke 0 (egyáltalán nem tartozik bele a klaszterbe) és 1 (teljesen beletartozik) közé esik.
Léteznek ennél még finomabb különbségek:
- Szigorú felosztó klaszterezés: minden elem pontosan egy klaszterbe tartozik
- Szigorú felosztó klaszterezés outlierekkel: vannak olyan elemek, amik egyetlen klaszterbe sem tartoznak és ezek az outlierek
- Átfedő klaszterezés: az elemek több, mint egy klaszterbe tartozhatnak (nem kizáró klaszterezésnek is hívják)
- Hierachikus klaszterezés: azok az elemek, amik egy részei egy halmaznak, részei az azt a halmazt tartalmazó halmaznak is; ennél módszernél megengedjük, hogy a klasztereknek klasztereik lehessenek, de ha egy pontján elvágjuk a klaszterezési fát, akkor szintén szigorúan felosztó klaszterezéshez jutunk
Távolságmértékek[szerkesztés]
Láthattuk, hogy a különböző modellek szubjektíven értelmezik a hasonlóság fogalmát. A hasonlóság gyakran van kis távolságként definiálva, ilyenkor szükséges az, hogy meghatározzuk a távolság mértékét.
A klaszteranalízis során használt távolságmérték kiválasztása kritikusan fontos lépés, mert ez alapján fogja a klaszterelemzés meghatározni, hogy két elem mennyire hasonló egymáshoz. Így a kiválasztott távolságmérték befolyásolja az eredményül kapott klaszterek alakját is.
Gyakori távolságmértékek[szerkesztés]
- euklideszi távolság – leggyakrabban használt távolságfüggvény, intervallum és arány skálán mért metrikus adatoknál használható
- négyzetes euklideszi távolság
- Manhattan-távolság vagy abszolút eltérés
- Mahalanobis-távolság – általánosítja a standardizációs eljárást, figyelembe veszi a nem független változóknál a korreláció mértékét
- Hamming-féle távolság (a behelyettesítések minimális száma, amivel az egyik tag átváltható a másikba)
- Pearson-távolság – nem összemérhető változóknál, standardizálással számolva
Fontos szempont lehet a klaszterelemzés során, hogy szimmetrikus vagy aszimmetrikus távolságokat használunk-e. Az euklideszi távolság például szimmetrikus („A” távolsága „B”-től ugyanakkora, mint „B” távolsága „A”-tól). Más esetekben a távolság nem szimmetrikus (lásd például Prinzie & Van den Poel (2006)).
A klaszterelemzés fajtái[szerkesztés]
A klaszterelemzés algoritmusa lehet hierarchikus vagy nem hierarchikus. A hierarchikus algoritmus az új klasztereket az előzőleg kialakított klaszterek alapján keresi meg, míg a nem hierarchikus algoritmus egyszerre határozza meg az összes klasztert.
Hierarchikus klaszterelemzés[szerkesztés]
A hierarchikus klaszterezés lehet összevonó (Agglomerative) és felosztó (Divisive). Az összevonáson alapuló algoritmus először minden egyes elemet külön klaszternek tekint és összekapcsolja őket egyre nagyobb klaszterekbe, míg a végén egyetlen, az összes elemet tartalmazó klasztert kapunk. A felosztáson alapuló algoritmus ezzel ellentétben először az egész adattömböt egyetlen klaszternek tekinti és egyre kisebb klaszterekre osztja, míg a végén minden elem külön klasztert képez. Az eredményt általában egy fa (dendrogram) formájában szokták ábrázolni, ahol az egyik végén az egyes elemek találhatóak, a másik végén pedig egyetlen klaszter, ami az összes elemet tartalmazza. Az összevonáson alapuló algoritmus a fa tetején kezdi az elemzést, a felosztáson alapuló pedig a gyökereknél. Ha elvágjuk a fát egy bizonyos magasságban, akkor azon az adott ponton megpróbálhatjuk értelmezni a klaszterezés eredményét.
Példa az összevonáson alapuló hierarchikus klaszterezésre[szerkesztés]
Nézzük például az alábbi adatokat, melyeket csoportosítani szeretnénk:

Az alábbi dendrogramon látható, hogy ez a módszer úgy építi fel a hierarchiát az egyes elemekből, hogy egyre jobban összeolvasztja a klasztereket. Ebben a példában hat elem van: {a}, {b}, {c}, {d}, {e} és {f}. Az ábráról láthatjuk, hogy az algoritmus először összekapcsolta a két legközelebbi elemeket, a {b}-t és a {c}-t, valamint a {d}-t és az {e}-t. Ekkor a következő klasztereink vannak: {a}, {b, c}, {d, e} és {f}. Ezután a {d, e} klasztert a legközelebbi, leginkább hasonló elemmel, az {f}-fel kapcsolja össze. Ezen a szinten már csak három klaszterünk van: {a}, {b, c} és {d, e, f}.
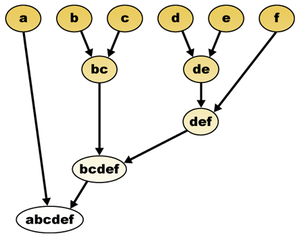
A következő lépésben a {b, c} és a {d, e, f} klaszterek esnek a legközelebb egymáshoz, ezért ezekből jön létre egy új, nagy klaszter. Most már csak két klaszterünk van, az {a} és a {b, c, d, e, f}. Az összevonáson alapuló eljárás végeredményeként pedig egyetlen nagy klaszter jön létre, mely tartalmazza az összes elemet: {a, b, c, d, e, f}.
Korlátok[szerkesztés]
A hierarchikus klaszterelemzésnek megvannak a saját korlátai. A legfontosabbak közé tartozik, hogy két klaszter egyesítése nem visszafordítható, azaz utólag már nem módosítható. Ezenkívül a hierarchikus klaszterelemzés zaj és kiugró értékek iránti érzékenysége nagy, valamint nehezen kezeli a konvex alakú és a jelentősen eltérő méretű klasztereket, és a nagy klasztereket hajlamos feldarabolni (Dr. Obádovics Csilla, 2009 alapján). Végül, a hierarchikus klaszterelemzés csak folytonos, metrikus változókon alkalmazható (Venables and Ripley, 2002.)
Az összevonáson alapuló (agglomeratív) klaszterelemzés fajtái[szerkesztés]
Az összevonáson alapuló klaszterelemzésen belül különböző csoportosítási módszereket különböztetünk meg: a lánc-, a variancia- és a centroidmódszert.
- ’’’Egyszerű láncmódszer’’’ (Single linkage clustering): A legközelebbi szomszéd (en: Nearest neighbor) elvén alapuló eljárás. Két klaszter közötti távolságot a két legközelebbi elem távolsága alapján számolja ki.
- ’’’Teljes láncmódszer’’’ (Complete linkage clustering): A legtávolabbi szomszéd (en: Furthest neighbor) elvén alapuló eljárás. Két klaszter közötti távolságot a két legtávolabbi elem távolsága alapján határozza meg.
- ’’’Átlagos láncmódszer’’’ (Average linkage clustering): Két klaszter távolságát az összes elem páronkénti távolságának átlaga alapján határozza meg, ahol a pár egyik eleme az egyik klaszterbe, a másik eleme pedig a másik klaszterbe tartozik. Mivel ez az eljárás nem csak a legkisebb és legnagyobb távolságot használja fel, ezért általában előnyben részesítik a másik két láncmódszerrel szemben.
- ’’’Varianciamódszer’’’: A Ward-féle eljárás az egyik leggyakrabban alkalmazott módszer, mely azokat a klasztereket vonja össze, melyeknél az összevonás során a legkisebb lesz a belső szórásnégyzet növekedése.
- ’’’Centroidmódszer’’’: Két klaszter közötti távolságot a klaszterek centroidja alapján határozza meg. A klaszterek centroidját a klaszterben benne foglalt összes pont aritmetikai átlaga adja. Ezt a módszert is gyakran használják a klaszterelemzés során.
Nem hierarchikus klaszterelemzés[szerkesztés]
K-közép klaszterelemzés[szerkesztés]
A nem hierarchikus klaszterelemzési módszerek közül a K-közép (en: K-means) algoritmus a legnépszerűbb. A K-közép algoritmus minden egyes elemet ahhoz a klaszterhez sorol, amelyiknek a középpontja a legközelebb esik az adott elemhez.
Az algoritmus lépései a következőek (MacQueen, 1967):
- Kiválasztja a klaszterek számát (k).
- Véletlenszerűen létrehoz k számú klasztert, és meghatározza minden klaszter közepét, vagy azonnal létrehoz k véletlenszerű klaszter középpontot.
- Minden egyes pontot abba a klaszterbe sorol, amelynek középpontjához a legközelebb helyezkedik el.
- Kiszámolja az új klaszter középpontokat.
- Addig ismétli az előző két lépést (iterál), amíg valamilyen konvergencia kritérium nem teljesül (általában az, hogy a besorolás nem változik).
Az algoritmus legnagyobb előnye az egyszerűsége és a sebessége, ami lehetővé teszi az alkalmazását nagy adattömbön is. Hátránya viszont, hogy nem ugyanazt az eredményt adja különböző futtatások után, mert a klaszterezés eredményét befolyásolja a kezdeti random besorolás. Minimálisra csökkenti a klasztereken belüli varianciát, de nem eredményezi összességében a legkisebb varianciát.
Hierarchikus vagy nem hierarchikus klaszterezést használjunk? (Sajtos és Mitev (2007) alapján)[szerkesztés]
A nem hierarchikus módszereket akkor érdemes használni, ha sok adatunk van és a kapott eredmények kevésbé függnek a kiugró adatoktól és a kiválasztott távolságmértéktől. Ha azonban nem hierarchikus módszert választunk, előre meg kell adni a klaszterek számát és a klaszterközéppontokat. A hierarchikus módszerek végrehajtása nagy adatbázis esetében hosszadalmas lehet, és e módszerek érzékenyebbek a kiugró értékekre. Előnye azonban, hogy lehetővé teszi a klaszterek grafikus megjelenítését dendrogram formájában, ami jelentős segítséget nyújt a klaszterek számánál kiválasztásánál és az eredmények értelmezésénél. Ajánlott a hierarchikus és a nem hierarchikus módszereket egyszerre alkalmazni. Például először egy hierarchikus algoritmussal meghatározzuk a klaszterek számát, a klaszterközéppontokat, kiszűrjük a kiugró adatokat, majd a nem hierarchikus eljárással újracsoportosítjuk az adatokat.
Döntés a klaszterek számáról és az elemzés megbízhatóságáról[szerkesztés]
A klaszterek számának megválasztása döntési probléma, nincs rá egyetlen elfogadott eljárás. Az egymást követő lépéseknél adódó klaszterek közötti távolság jó irányadó lehet. Akkor célszerű megállni, amikor pl. a távolságérték túllép egy bizonyos értéken, vagyis amikor a soron következő távolság jóval nagyobb az előzőeknél, hirtelen ugrás következik. (Obádovics, (2009) alapján)
A klaszterelemzés eredményeképpen kapott csoportok jóságát, validitását többféleképpen lehet értékelni, de ez gyakran éppoly nehéz feladat, mint a klaszterezés maga. A népszerű megközelítések közé tartozik a “belső” (internal) értékelés, amikoris a klaszterezés összesítve lesz egyetlen kvalitás értékbe, és a “külső” (external) értékelés, amikor a klaszterezés egy már létező, “alapvető igazság” osztályozáshoz van hasonlítva, a “kézi” (manuális) értékelése egy emberi szakértőnek, és az “indirekt” értékelés, amikor a klaszterek a későbbi alkalmazáskor tanúsított hasznosságuk alapján kerülnek értékelésére.
Mind a belső, mind a külső értékelésű mérőeszközöknek számos korlátja van. Előbbi nem mutat arra rá, hogy mennyire hasznos maga klaszterezés, míg utóbbi gyakran nem létező, vagy nem biztos, hogy a létező lehető legjobb címkékhez méri a klaszterezést, ami által az eredmény nem jelenti azt, hogy nem létezik egy másfajta, éppenséggel jobb klaszterezés.
Így a klaszterezés minőségét az emberi, erősen szubjektív értékelés tudja csak megmondani. Ez utóbbi megtartása mellett, a különböző értékelések hasznosak lehetnek a rossz klaszterezések azonosítására.
A klaszterelemzés alkalmazási területei[szerkesztés]
Biológia[szerkesztés]
A klaszterelemzés rendkívül népszerű eljárás, melyet gyakran használnak például az ökológiában növény- és állatközösségek csoportosítására heterogén környezetben, növényrendszertanban egyedek csoportjainak meghatározására faj, család stb. szintjén. A bioinformatikán belül például a hasonló expressziós mintázatot létrehozó gének klaszterezésénál alkalmazzák.
Ökológia[szerkesztés]
A klaszteranalízis térbeli és időbeli összehasonlítására szolgálhat heterogén környezetben élő szervezetek közösségeire. Szintén használt növényi rendszertanban mesterséges törzsfejlődés képzésére vagy organizmusok faji, nemzetségi vagy fentebbi szintű, azonos tulajdonságokban osztozó klaszterekbe csoportosítására.
Transzkriptomiksz[szerkesztés]
Klaszterezés használható különbözően kifejeződő gének csoportjainak megalkotására.
Emberi genetikai klaszterezés[szerkesztés]
A genetikus adatok hasonlóságágból klaszterezéssel következtethetünk a populáció struktúrájára.
Orvoslás[szerkesztés]
Orvosi képalkotás[szerkesztés]
PET képeknél a klaszteranalízis használható a különböző típusú szövetek megkülönböztetésére háromdimenziós képeknél.
Antimikrobális tevékenység elemzése[szerkesztés]
Klaszteranalízis használható az antibiotikus rezisztencia mintázatok elemzésére, vagyis osztályozni az antimikrobális vegyületeket a hatás-mechanizmusuk alapján, illetve osztályozni az antibiotikumokat az antibakteriális hatásuk alapján.
Bölcsészettudomány[szerkesztés]
A stilometria a különböző szövegek közötti hasonlóságok és különbségek elemzésére használja. Alkalmas lehet például ismeretlen szerzőjű szövegek szerzőjének azonosítására.
Informatika[szerkesztés]
A képfeldolgozásban a klaszterelemzés igénybevételével azonosíthatóak az élek vagy a tárgyak a képeken. A klaszterezés segítségével a weboldalak, webes keresési eredmények csoportokba rendezésénél relevánsabb szempontokat alkothatunk (szemben például a hagyományos keresőprogramokkal), vagy például internetes boltok termékeit is csoportosíthatjuk.
Üzlet és marketing[szerkesztés]
Piackutatás[szerkesztés]
A klaszteranalízis széleskörűen alkalmazott piackutatások során, többváltozós tesztadatokkal dolgozva. A piackutatók általában arra használják a klaszteranalízist, hogy a fogyasztókat piacszegmensekbe osszák, és így jobban megértsék a különböző fogyasztói csoportok közti kapcsolatokat és ez piacszegmentációra, termék pozícionálásra, új termékek kifejlesztésére és teszt piacok kiválasztására felhasználják
Eladó termékek csoportosítása[szerkesztés]
A klaszterezés arra is alkalmas, hogy az összes interneten elérhető terméket egyedi termékek csoportjaira bontsa.
Internet[szerkesztés]
Közösségi hálózat analízis[szerkesztés]
Közösségi hálózatok tanulmányozása során a klaszterezés képes lehet közösségek azonosítására nagyobb embercsoportokon belül
Keresési eredmények csoportosítása[szerkesztés]
A klaszterezés alternatívát jelenthet a hagyományos keresőmotoroknak, mivel képes arra, hogy csoportosítsa a megtalált weboldalakot és fájlokat, és ezáltal relevánsabbá tegye a keresési eredményeket (például csoportosíthatja a találatokat, amikor a keresőszó több különböző dologra is utalhat).
Társadalomtanulmányok[szerkesztés]
A piackutatásban gyakran alkalmazott módszer például a piacszegmentálás során (amikor a fogyasztókat különböző csoportokba sorolják), piacszerkezet-elemzésnél, új termék lehetőségeinek feltárásánál, tesztpiacok kiválasztásánál. A klaszterelemzés kiválóan használható szociális hálózatok elemzésénél, amikor emberek nagy csoportját szeretnénk kisebb közösségekbe sorolni.
Bűnelemzés[szerkesztés]
Klaszterelemzéssel azonosíthatók olyan területek, ahol gyakrabban fordulnak elő bizonyos típusú bűnügyek, ezáltal kialakítva úgynevezett forró pontokat, ami lehetővé teszi a bűnmegelőzési erőforrások hatékonyabb allokációját. Az igazságügyi nyelvészet a stilometriai klaszterelemzéssel képes lehet azonosítani egy szöveg szerzőjét.
Képzési célú adatbányászat
A klaszteranalízis használható arra, hogy iskolák vagy tanulók azonos tulajdonságokkal rendelkező csoportjait azonosítsuk.
Tipológiák[szerkesztés]
Közvélemény-kutatási adatokból klaszterelemzéssel kinyerhetők véleményekre, szokásokra, és demográfiára vonatkozó tipológiák, amik hasznosak lehetnek a politikában és marketingben.
Egyéb[szerkesztés]
A klaszterelemzés hasznos megoldás olyan tudományterületeknél is, mint a robotika, matematikai kémia, klímakutatás, geográfia
Irodalom[szerkesztés]
- Fülöp, A- (2006). Klaszteranalízis: Alapvető fogalmak és algoritmusok, in: Tan, P., Steinbach M., Kumar V. (2006) Bevezetés az adatbányászatba
- MacQueen, J. B. (1967). Some Methods for classification and Analysis of Multivariate Observations, Proceedings of 5-th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, University of California Press, 1:281-297
- Obádovics, Cs. (2009). Klaszteranalízis
- Prinzie, A & Van den Poel, D. (2006). Incorporating sequential information into traditional classification models by using an element/position-sensitive SAM. Decision Support Systems 42 (2): 508-526.
- Sajtos, L. & Mitev, A. (2007). SPSS kutatási és adatelemzési kézikönyv. Aliena Kiadó, Budapest.
- Székelyi, M. & Barna, I. (2002). Túlélőkészlet az SPSS-hez. Többváltozós elemzési technikákról társadalomkutatók számára. Typotex Kiadó, Budapest.
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a Cluster_analyses című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Források[szerkesztés]
- Magyar nyelvű leírás a klaszterelemzésről: https://web.archive.org/web/20140923060356/http://nti.btk.pte.hu/dogitamas/BHF_FILES/html/08Munnich/pages/p_5_1.xml
- Példa a biológiai alkalmazásra: http://www.hik.hu/tankonyvtar/site/books/b137/ch03s03s02s02.html Archiválva 2008. április 11-i dátummal a Wayback Machine-ben
- Példa közgazdaságtani alkalmazásra:
- https://web.archive.org/web/20090509150820/http://www.inf.unideb.hu/valseg/dolgozok/ispany/Multivar/main.html
- Példa a piackutatási alkalmazásra:
- http://www.lib.uni-corvinus.hu/phd/kunsagi_andrea.pdf[halott link],
- http://phd.lib.uni-corvinus.hu/253/01/harsanyi_gabor.pdf

