Kardáncsukló

A kardáncsukló két rúd (tengely) közötti olyan kapcsolat, mely lehetővé teszi azt, hogy egymáshoz képest hajlítónyomaték ébredése nélküli minden irányban elhajoljanak, de meggátolja a két rúd egymáshoz képesti elcsavarodását és így lehetőség nyílik forgatónyomaték átvitelére egyik tengelyről a másikra. Más definíció szerint a kardáncsukló négytagú csuklós gömbi mechanizmus.
A kardáncsukló központi eleme az úgynevezett kardánkereszt, mely lényegében két egymásra merőleges csap-párból áll, melyek a tengelyek végére szerelt vagy azokkal egy darabból kiképzett villákhoz csatlakoznak csapágyakon keresztül.
Története[szerkesztés]
A kardáncsukló elve a kardán-felfüggesztés használata során merült fel, ami már az ókortól ismeretes volt. Egyik alkalmazása az ókori görögök által feltalált ostromgép, ballista esetén ismert. 1545-ben Gerolamo Cardano olasz matematikus volt az első, aki a kardáncsuklót hajtásra javasolta, de kétséges, hogy kivitelezte-e valaha is. Később Christopher Polhem svéd tudós és vállalkozó ismét feltalálta, majd 1676-ban Robert Hooke készített egy működő kardáncsuklót. Európában főként kardáncsuklónak nevezik a mechanizmust, de a fentiek miatt angolszász nyelvterületen gyakran Polhem-csukló, Hooke-csukló vagy univerzális csukló a neve. Ez utóbbi először Henry Ford egyik szabadalmában jelenik meg a 19. század végén.
Mozgásegyenletei[szerkesztés]
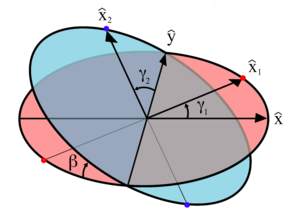
A kardáncsukló helyzetét három változóval lehet jellemezni:
- az 1. tengely szögelfordulása,
- a 2. tengely szögelfordulása,
- a tengelyek egymáshoz képesti hajlásszöge: nulla, ha a két tengely egybeesik.
Ezek a változók az ábrán láthatók. Ugyancsak látható egy rögzített koordináta-rendszer és egységvektora valamint a két tengelyre merőleges, ugyancsak rögzített sík. A két tengelyt összekapcsoló kardánkereszt és a két villa az ábrán nincs feltüntetve. Az 1. tengely a piros sík piros pontjain, a 2. tengely pedig a kék sík kék pontjain csatlakozik a kardánkereszthez. A forgó tengelyekhez rögzített x koordinátatengelyeket egységvektoraikkal ( and ) jelöltük, melyek az origótól a csatlakozási pontjuk felé mutatnak. Az ábrából látható, hogy a elfordulási szöge az x tengelytől számított kezdeti helyzetéhez képest és elfordulási szöge pedig az y tengelyhez képest. A két tengely (és a így a kék és piros sík is) egymással szöget zár be.
Az a piros síkban mozog és a szöggel így fejezhető ki:
Az a kék síkban mozog és az x tengely egységvektorának a ] Euler-szögekkel való elforgatásának eredménye:
A és tengelyekre felírható kényszer az, hogy a kardánkereszt miatt merőlegesnek kell lenniük egymásra:
Így a két szöghelyzettel kifejezett mozgásegyenlet:
A és szög egy forgó csuklónál az idő függvénye lesz. Ha a mozgásegyenletet az idő szerint deriváljuk, és magával a mozgásegyenlettel az egyik változót kiküszöböljük az és szögsebesség közötti összefüggést kapjuk:

|

|
| A hajtott tengely szögsebessége a szög függvényében | A hajtott tengely szögelfordulása a hajtó tengely szögelfordulásának függvényében |

Az ábrán látható, hogy állandó behajtó tengely szögsebesség mellett a kimenő tengelyen a szögsebesség periodikusan változik, mégpedig a behajtó tengely frekvenciájának kétszeresével. Ha a szögsebesség függvényét az idő szerint tovább deriváljuk, az és szöggyorsulás közötti összefüggéshez jutunk:
Alkalmazása[szerkesztés]
A kardáncsuklót gyakran alkalmazzák olyan helyeken, ahol egymáshoz szögben hajló tengelyeket kell összekötni. Ilyen például az olyan szelepek mozgatása, mely a kezelőhelytől nem elérhető távolságban (1–2 m) van. Ilyen és hasonló, lassú tengelymeghajtásra a kardáncsuklóval kapcsolt tengelyek teljesen megfelelnek. Más a helyzet akkor, ha a hajtásnak nagyobb fordulatszámon jelentős teljesítményt kell átvinnie, például járművek hajtáslánca esetén. Ilyenkor ugyanis a kardáncsukló káros rezgéseket gerjeszthet, mely vagy a működés szempontjából nemkívánatos, vagy a hajtás idő előtti kifáradását okozza. Az ilyen esetekben csaknem kiküszöbölhető a szögsebesség változása, ha a hajtott és hajtó tengely párhuzamosan helyezkedik el és egy harmadik tengely egy-egy kardáncsuklóval a végén kapcsolja össze velük. Ez a megoldás a legtöbb gépkocsinál, nagyon sok vasúti hajtásnál elterjedt megoldás, annál is inkább, mert lehetővé teszi, hogy a két tengely egymáshoz képest el is mozduljon (természetesen betartva a tengelyek párhuzamosságát), ezzel ugyanis a kerekek és a motor közötti rugózás egyszerűen megoldható.
A gyakorlatban sokszor nem lehet betartani pontosan a fenti geometriai követelményeket, ilyenkor a hajtás rugalmasságának fokozásával lehet csökkenteni a káros gerjesztés hatását. Az egyik ilyen jól bevált módszer a Hardy-tárcsa alkalmazása. A Hardy-tárcsa a kardáncsuklót helyettesítő tengelykapcsoló, mely a kardáncsukló helyett rugalmas elemet használ (kordszövettel erősített gumilemezeket), mely azonban nemcsak a hajlítás irányában rugalmas, hanem kisebb mértékben csavarásra is rugalmasan kitér.
Források[szerkesztés]
- Muttnyánszky Ádám: Kinematika és kinetika. Tankönyvkiadó, Budapest 1957.
- Pattantyús Gépész- és Villamosmérnökök Kézikönyve 2. kötet. Műszaki Könyvkiadó, Budapest, 1961.
Külső hivatkozások[szerkesztés]
- Kabai Sándor kardáncsukló szimulációja (The Wolfram Demonstrations Project).








![{\displaystyle {\hat {\mathbf {x} }}_{1}=[\cos \gamma _{1}\,,\,\sin \gamma _{1}\,,\,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a64cba968b7024287cf4ff0b7b5c84ebaab8bad9)
![{\displaystyle {\hat {x}}=[1,0,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bd3be5ddf79743233234f9f2af9943acc1aa0a7)

![{\displaystyle {\hat {\mathbf {x} }}_{2}=[-\cos \beta \sin \gamma _{2}\,,\,\cos \gamma _{2}\,,\,\sin \beta \sin \gamma _{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e880dc9a98c0dd932d775f23b8bee4642451847d)










