Elvágó csúcshalmaz
A matematika, azon belül a gráfelmélet területén csúcsok egy részhalmaza a nem szomszédos és csúcsok tekintetében elvágó csúcshalmaz vagy elvágó ponthalmaz (angol nyelvterületen: vertex separator, vertex cut, separating set), ha a gráfból -t eltávolítva és különböző összefüggő komponensekbe kerülnek. Általánosabb megfogalmazásban: egy gráf elvágó csúcshalmaza csúcsok olyan halmaza, melyek elhagyásával a maradék gráf szétesik.
Példák[szerkesztés]

Tekintsünk egy s sorral és o oszloppal rendelkező rácsgráfot; ekkor a csúcsok n darabszáma éppen s · o. Például az illusztrációban s = 5, o = 8 és n = 40. Ha s páratlan, egyetlen középső sor van, egyébként két a középhez egyformán közel húzódó sor található; hasonlóan, ha o páratlan, egyetlen középső oszlop van, egyébként két a középhez egyformán közel húzódó oszlop van. Ha az S-t ezen középső oszlop vagy sor csúcsaiból választjuk ki, az S gráfból való eltávolítása a gráfot két kisebb, egyenként összefüggő A és B részgráfra osztja, melyek mindegyike legfeljebb n/2 csúcsból áll. Ha s ≤ o (ahogy a példában szerepel), a középső oszlopot választva az S csúcsainak száma s ≤ √n; hasonlóan, ha o ≤ r, akkor egy középső sort választva az elvágó ponthalmaz elemeinek száma legfeljebb √n. Tehát minden rácsgráf rendelkezik legfeljebb √n csúcsból álló S elvágó ponthalmazzal, melynek eltávolítása a gráfot két, legfeljebb n/2 méretű összefüggő komponensre osztja.[1]
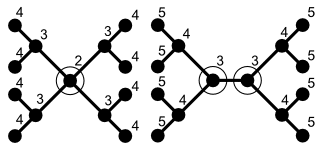
Egy más jellegű példa: minden T szabad fa rendelkezik egy olyan S elvágó csúcshalmazzal, ami egyetlen csúcsból áll, és aminek eltávolítása T-t két vagy több összefüggő, legfeljebb n/2 méretű komponensre bontja. Precízebben, minden fa esetében pontosan egy vagy pontosan két ilyen csúcs létezik, attól függően, hogy a fa egy vagy két középpontú (centered, bicentered).[2]
Az előbbi példák annyiból kivételesnek tekinthetők, hogy nem minden elvágó csúcshalmaz „kiegyensúlyozott”. de ez a tulajdonság a legtöbb számítástudományi alkalmazásban hasznosnak bizonyul, pl..
Minimális elvágó halmazok[szerkesztés]
Legyen S egy (a,b)-szeparátor, tehát a nem szomszédos a és b csúcsokat elvágó csúcshalmaz. Az S akkor minimális (a,b)-elvágó csúcshalmaz, ha S-nek egyetlen valódi részhalmaza sem elvágó csúcshalmaz a és b tekintetében. Általánosabban, S minimális elvágó csúcshalmaz, ha valamely (a,b) nem szomszédos csúcsokra nézve minimális elvágó csúcshalmaz. A κ(a, b) lokális összefüggőség az a és b csúcsokhoz tartozó minimális elvágó csúcshalmaz mérete.
A minimális elvágó csúcshalmazokat karakterizáló jól ismert eredmény a következő:[3]
Lemma. Egy G gráf S elvágó csúcshalmaza akkor és csak akkor minimális, ha az S G-ből való eltávolításával kapott gráf rendelkezik két összefüggő és komponenssel, amikre igaz, hogy minden S-beli csúcs szomszédos valamely -beli és valamely -beli csúccsal is.
A minimális elvágó csúcshalmazok algebrai struktúrát is alkotnak: adott G gráf kiválasztott a és b csúcsára nézve valamely S (a,b)-elvágó csúcshalmaz egy másik T (a,b)-elvágó csúcshalmaz elődjének tekinthető, ha minden a és b közötti út először S-t érinti, mielőtt T-t érintené. Ennél precízebben fogalmazva az előd reláció a következőképpen definiálható: legyen S és T két (a,b)-elválasztó csúcshalmaza G gráfnak. Ekkor S elődje T-nek, azaz , ha minden esetében, az x-et b-vel összekötő összes út érinti T-t. A definícióból következik, hogy az előd reláció előrendezést eredményez az (a,b)-elvágó csúcshalmazok halmazán. Továbbá (Escalante 1972) igazolta, hogy az előd reláció teljes hálót eredményez, ha G gráf minimális (a,b)-elvágó csúcshalmazaira korlátozzuk.
Kapcsolódó szócikkek[szerkesztés]
- Húrgráf, olyan gráf, melynek minden minimális elvágó csúcshalmaza klikk.
- k-szorosan összefüggő gráf
Jegyzetek[szerkesztés]
- ↑ (George 1973).
- ↑ (Jordan 1869)
- ↑ (Golumbic 1980).
- (1972) „Schnittverbände in Graphen”. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 38, 199–220. o. DOI:10.1007/BF02996932.
- George, J. Alan (1973), "Nested dissection of a regular finite element mesh", SIAM Journal on Numerical Analysis 10 (2): 345–363, DOI 10.1137/0710032.
- Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, ISBN 0-12-289260-7.
- Jordan, Camille (1869). „Sur les assemblages de lignes” (french nyelven). Journal für die reine und angewandte Mathematik 70 (2), 185–190. o.
- Graph Separators, with Applications. Springer. DOI: 10.1007/b115747 (2002)









