Labirintust létrehozó algoritmus
A labirintust létrehozó algoritmusok automatikus eljárások labirintusok létrehozására.

Gráf-elmélet módszerek[szerkesztés]
Labirintus létrehozható egy cellák előre meghatározott elrendezésével (leggyakrabban egy téglalap alakú rács, de más elrendezések is lehetséges), közöttük pedig falakkal. Ez az előre meghatározott elrendezés összefüggő gráfnak tekinthető, amelynek élei a lehetséges falhelyeket, a csomópontok pedig a cellákat képviselik. A labirintusgeneráló algoritmus célját tekinthetjük úgy, mint egy részgráf elkészítése, amelyben a kihívást az útvonal megtalálása jelenti két adott csomópont között.
Ha a részgráf nem összefüggő akkor bizonyos részei elvesznek, mert nem tartoznak a keresési területhez. Ha a gráf tartalmaz hurkokat, akkor számos út lehet a kiválasztott csomópontok között. Emiatt a labirintusgenerálást gyakran úgy közelítjük meg, hogy létrehozzunk egy random feszítőfát. A hurkok, melyek megtéveszthetik az egyszerű megoldásokat, létrehozhatóak úgy, hogy az algoritmus során véletlenszerűen éleket adunk az eredményhez.
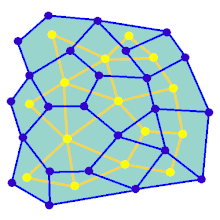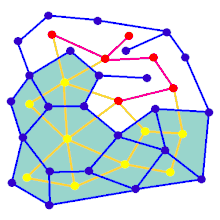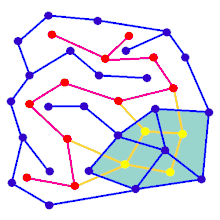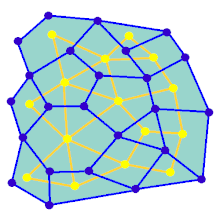
Az animáció egy gráf labirintusgenerációs lépéseit mutatja, mely nem téglalap rács. Először a számítógép egy véletlenszerű sík gráfot állít fel, amely kék színű, az ábrán a kettős gráf sárgán van jelölve. Ezután, a számítógép egy kiválasztott algoritmussal bejárja F-et, például egy mélység - keresés segítségével beszínezve pirossal az érintett utat. A bejárás során, amikor egy piros él áthalad egy kék élen, a kék élt eltávolítják. Végül, amikor az F összes csúcsát bejártuk, az F és G két éle, amik a be és kiindulásnak felelnek meg, törlésre kerülnek.
Mélységi keresés[szerkesztés]
Ez az algoritmus a mélységi keresés algoritmusnak egy véletlenszerű verziója. Ez a megközelítés, amelyet gyakran veremben valósítanak meg, az egyik legegyszerűbb módszer egy labirintus létrehozására számítógéppel. Tekintsük a labirintust egy nagy rácsnak (mint egy nagy sakktábla), ahol mindegyik cella négy fallal rendelkezik kezdetben. Egy véletlenszerű cellától kiindulva a számítógép kiválaszt egy szomszédos cellát, amelyet még nem vizsgált meg. A számítógép eltávolítja a két cella közti falat, megvizsgáltként jelöli meg ezt a cellát, és hozzáadja azt egy veremhez, a visszakeresés megkönnyítése érdekében. A számítógép folytatja ezt a bejárást egy olyan cellával, aminek nincs meg nem megvizsgált szomszédja, amit zsákutcának hívunk. A zsákutcában visszafelé halad az útvonalon, amíg egy cellához nem ér, aminek már van megvizsgált szomszédja, és folytatja az út generálását ezzel a cellával (új kereszteződés létrehozása). Ez a folyamat mindaddig folytatódik, amíg minden cellát be nem járt, aminek eredményeként a számítógép visszafelé halad a kezdő celláig. Így biztosak lehetünk abban, hogy minden cellát bejártunk.

A fentiek következtében ez az algoritmus olyan rekurziót alkalmaz, amely verem túlcsordulási problémákat okozhat egyes számítógépes architektúrákban. Az algoritmus hurokba rendezhető úgy, hogy a visszalépési információkat a labirintusban tárolja. Ez gyors megoldást kínál a megoldás megjelenítésére is, egy adott pontról indulva, és visszalépkedve a kiinduló ponthoz.

A mélységi kereséssel létrehozott labirintusok alacsony elágazási tényezővel rendelkeznek, és sok hosszú folyosót tartalmaznak, mivel az algoritmus a lehető legjobban feltárja az egyes ágakat, mielőtt visszalépne.
Ismétlődő visszalépéses keresés[szerkesztés]
A labirintusgeneráló mélységi keresés algoritmus gyakran jön létre visszalépéses kereséssel. Ezt az alábbi rekurzió szemlélteti:
- Adott egy aktuális cella paraméterként,
- Jelöljük az aktuális cellát meglátogatottként,
- Míg a jelenlegi cellának van még nem látogatott szomszédja.
- Válasszunk egyet ezek közül!
- Távolítsuk el a falat az aktuális cella és a kiválasztott cella között!
- Alkalmazzuk a folyamatot rekurzívan a kiválasztott cellára, amelyet egyszer meghívnak a terület bármely kezdeti cellájára.
Ennek a megközelítésnek a hátránya a rekurzió nagy mélysége - a legrosszabb esetben a rutinnak meg kell ismételnie a feldolgozandó terület minden celláját, amely sok környezetben meghaladhatja a maximális rekurziós verem mélységet. Megoldásként ugyanaz a visszavonási módszer valósítható meg egy explicit veremmel is, amely általában megengedi, hogy sokkal nagyobb legyen, hiba nélkül.
- Válasszuk ki a kezdő cellát, jelöljük meg meglátogatottként, és tegyük bele a verembe!
- Amíg a köteg nem üres
- Nyissunk meg egy cellát a veremből, és tegyük aktuális cellává!
- Ha az aktuális cellában van meg nem látogatott szomszédja
- Tegyük az aktuális cellát a verembe!
- Válasszunk egyet a meg nem látogatott szomszédok közül!
- Távolítsuk el a falat az aktuális cella és a kiválasztott cella között!
- Jelöljük meg a kiválasztott cellát meglátogatottként, és tegyük a verembe!
Véletlenszerű Kruskal-algoritmus[szerkesztés]
Ez az algoritmus Kruskal algoritmusának véletlenszerű változata.
- Készítsünk egy listát az összes falról, és hozzunk létre egy halmazt minden cellához, amelyek mindegyike csak azt a cellát tartalmazza!
- Minden falhoz, véletlenszerű sorrendben:
- Ha a fal által osztott cellák különálló halmazokba tartoznak:
- Távolítsuk el az aktuális falat!
- Egyesítsük a korábban osztott cellák halmazát!
- Ha a fal által osztott cellák különálló halmazokba tartoznak:
Számos adatszerkezet használható a cellakészletek modellezésére. Egy hatékony megvalósítás a diszjunkt halmaz adatszerkezet használata ami két halmazon közel constans időben tudja elvégezni az unio és keresés műveleteket, (különösen, idő; minden valószínű értékre ), így a futási idő arányos a rendelkezésre álló falak számával.
Nem számít, hogy a falak listája kezdetben véletlenszerűen van-e kiválasztva, vagy egy falat véletlenszerűen választanak meg egy nem véletlenszerű listából, mindkét esetben könnyű kódolni.
Mivel az algoritmusnak lényege egy minimális feszítőfát készítsen egy azonos él súlyokkal rendelkező gráfból, ezért általában olyan szabályos mintákat állít elő, amelyeket meglehetősen könnyű kezelni.
Véletlenszerű Prim-algoritmus[szerkesztés]
Ez az algoritmus a Prim algoritmusának véletlenszerű változata.
- Kezdjük egy falakkal teli ráccsal!
- Válasszunk egy cellát, jelöljük meg a labirintus részeként!
- Adjuk hozzá a cella falait a fallistához!
- Amíg vannak falak a listában:
- Válasszunk egy véletlenszerű falat a listából! Ha a fal által határolt két cella közül csak az egyik volt meglátogatva akkor:
- Készítsünk egy átjárót, és jelöljük meg a meg nem látogatott cellát a labirintus részeként!
- Adjuk hozzá a cella szomszédos falait a fallistához!
- Távolítsuk el a falat a listáról!
- Válasszunk egy véletlenszerű falat a listából! Ha a fal által határolt két cella közül csak az egyik volt meglátogatva akkor:
Általában viszonylag könnyű megtalálni az utat a kiindulási cellához, de nehéz megtalálni máshoz.
Vegyük figyelembe, hogy ha a klasszikus Prim-algoritmust futtatjuk véletlenszerű élsúlyú gráfon, akkor azok a labirintusok hasonlóak lesznek, mint a Kruskal alkalmazásával, mivel mindkettő egy minimális feszítőfát létrehozó algoritmus. Ehelyett ez az algoritmus stílusszerű változatokat alkalmaz, mivel a kezdőponthoz közelebb lévő éleknek kisebb a tényleges súlyuk.
Módosított változat[szerkesztés]
Noha a klasszikus Prim-algoritmus megtartja az élek listáját, labirintus létrehozáshoz ehelyett inkább csak a szomszédos cellák listáját tartjuk meg. Ha a véletlenszerűen kiválasztott cellának több éle van, amely összeköti azt a meglévő labirintussal, akkor véletlenszerűen válassza ki ezen élek egyikét. Ez általában kicsivel jobban elágazik, mint a fenti változat.
Wilson algoritmusa[szerkesztés]
A fenti algoritmusok különféle torzításokkal rendelkeznek: a mélységi keresés a hosszú folyosók felé tolódik el, míg Kruskal/Prim algoritmusai sok rövid zsákutcába juthatnak. Wilson algoritmusa[1] ezzel szemben egy, az összes labirintusból álló általános mintát generál, és hurokeltávolító sétákat használ.
Az algoritmust azzal kezdjük, hogy a labirintust egy tetszőlegesen kiválasztott cellával inicializáljuk. Ezután egy másik tetszőlegesen kiválasztott cellától indulunk ki, és véletlenszerű sétát folytatunk, amíg el érünk egy cellát, ami a labirintusban van. Azonban, ha a séta bármely ponton eléri a saját útját, hurkot képezve, töröljük a hurkot mielőtt folytatnánk az utat, aztán egy újabb hurok eltávolító sétát teszünk egy másik tetszőleges cellától indulva, addig ismételve a folyamatot, amíg minden cella ki nincs töltve.
Ez az eljárás torzítatlan marad, függetlenül attól, hogy milyen módszerrel választjuk ki a kezdőcellákat. Tehát mindig kiválaszthatjuk például az első ki nem töltött cellát (mondjuk) balról jobbra és fentről lefelé az egyszerűség kedvéért.
Rekurzív osztásmódszer[szerkesztés]
| eredeti kamra | két falra osztva | lyukak a falakban | folytassa a felosztásukat. . . | befejezték |
|---|---|---|---|---|
 |
 |
 |
 |
 |
Labirintusok létrehozhatók rekurzív osztásos algoritmussal, amely a következőképpen működik: Kezdjük egy olyan hellyel, ahol nincsenek falak. Hívjuk ezt egy kamrának. Osszuk fel a kamrát véletlenszerűen elhelyezett fallal (vagy falakkal), ahol minden fal véletlenszerűen elhelyezett átjárót tartalmaz. Ezután rekurzívan ismételjük meg a folyamatot az al-kamrán, amíg az összes kamra minimális méretű lesz. Ez a módszer olyan labirintusokat eredményez, amelyekben hosszú, egyenes falak keresztezik a helyeket, így könnyebben látható, mely területeket kell elkerülni.

Például egy téglalap alakú labirintusban véletlenszerűen készítsünk két, egymásra merőleges falat. Ez a két fal felosztja a kamrát négy kisebb, fallal elválasztott kamrára. Válasszunk véletlenszerűen a négy fal közül a hármat és nyissunk egy egy fal széles lyukat mindhármon. Folytassa ezt a módszert rekurzív módon mindaddig, amíg minden kamra egy cella szélességű nem lesz bármely két irányban.
Egyszerű algoritmusok[szerkesztés]

Léteznek más, olyan egyszerű algoritmusok, melyek csak annyi memóriát igényelnek, hogy eltárolják a 2D labirintus egy falát, vagy 3D esetben a síkot. Eller algoritmusa meggátolja a hurkok kialakulását azáltal, hogy eltárolja, az aktuális vonal mely cellái kapcsolódnak cellákhoz a korábbi vonalakkal, és sosem távolít el falakat már összekapcsolt két cella között.[2] A Sidewinder-algoritmus egy nyílt átjáróval indul az egész felső sor mentén, és a következő sorok rövidebb vízszintes szakaszokból állnak, amelyeknek egy összekapcsolása van a fenti átjáróval. A Sidewinder-algoritmus alulról felfelé megoldani triviális, mert nincs felfelé vezető zsákutca.[3] Adott kezdeti szélességgel mindkét algoritmus tökéletes labirintusokat hoz létre korlátlan magassággal.
A legtöbb labirintusgeneráló algoritmus megköveteli a kapcsolatok fenntartását a belsejében lévő cellák között annak biztosítása érdekében, hogy a végeredmény megoldható legyen. Érvényes, egyszerűen összekapcsolt labirintusok azonban generálhatók, azáltal, hogy csak az egyes cellákra külön-külön koncentrálunk. A bináris fa labirintus egy standard ortogonális labirintus, ahol minden egyes cellának mindig van egy átjárója, amely balra vagy felfelé vezet, de sosem mindkét irányba. Egy bináris fa labirintust létrehozásakor, minden egyes cellánál dobjunk fel egy pénzérmét annak eldöntésére, hogy balra vagy felfelé vezető utat adjunk e hozzá. Mindig ugyanazt az irányt válasszuk határon lévők cellák esetében, és a végeredmény egy egyszerűen összekapcsolt labirintus lesz, amely úgy néz ki, mint egy bináris fa, a bal felső sarokban egy gyökérrel. Mint a Sidewindernél, a bináris fa labirintusban nincs zsákutca az eltérítés irányában.
A pénzfeldobáshoz kapcsolódó formula egy olyan kép létrehozása, ami véletlenszerű egyvelegként használja a kétféle perjelet \ /. Ez nem hoz létre érvényes egyszerűen összekötött labirintust, inkább csak lezárt hurkokat és utakat. (A Commodore 64 kézikönyve BASIC-programot mutat be ezen algoritmus felhasználásával, de a sima grafikus megjelenés helyett PETSCII átlós vonal grafikus karaktereket használ.)
Sejtszerű automata algoritmusok[szerkesztés]
Bizonyos típusú celluláris automaták felhasználhatók labirintusok létrehozására. [4] Két jól ismert celluláris automata, a Maze és a Mazectric, B3 / S12345 és B3 / S1234 szabályokkal rendelkezik. Az előbbiben ez azt jelenti, hogy a cellák generációja túlél, ha legalább egy és legfeljebb öt szomszédjuk van . Az utóbbiban ez azt jelenti, hogy a sejtek életben maradnak, ha 1-4 szomszédjuk van. Ha egy cellának pontosan három szomszédja van, akkor létrejön. Ez hasonló a Conway életjátékhoz, annyiban, hogy ha nem létezik élő sejt 1, 4 vagy 5 más sejt mellett bármely generációban, akkor azonos módon viselkednek. A nagy minták esetében azonban nagyon eltérően viselkedik, mint az élet.
A véletlenszerű kiindulási mintázat érdekében ezek a labirintust generáló celluláris automaták komplex labirintusokká alakulnak, amelyek jól meghatározott falú folyosókat vázolnak fel. Labirintus központú, amelynek a B3 / S1234 szabálya van, hajlamos hosszabb és egyenes folyosókat generálni a Maze-hez képest, melynek B3/S12345 a szabálya.[4] Mivel ezek a celluláris automata szabályok determinisztikusak, az egyes generált labirintusokat egyedileg határozza meg véletlenszerű kezdési mintázata. Ez jelentős hátrány, mivel a labirintusok általában viszonylag kiszámíthatóak.
A fentiekben ismertetett gráfelméleti alapú módszerekhez hasonlóan, ezek a celluláris automaták általában útmutatásokat generálnak egyetlen kiindulási mintázatból; ennélfogva általában viszonylag könnyű megtalálni az utat a kiindulási cellához, de nehezebb megtalálni az utat máshol.
Irodalom[szerkesztés]
- ↑ Wilson, David Bruce (1996. május 22.). „Generating random spanning trees more quickly than the cover time”. Symposium on Theory of Computing: 296–303, Philadelphia: ACM. doi:10.1145/237814.237880.
- ↑ Jamis Buck: Maze Generation: Eller's Algorithm, 2010. december 29.
- ↑ Jamis Buck: Maze Generation: Sidewinder Algorithm, 2011. február 3.
- ↑ a b Nathaniel Johnston: Maze - LifeWiki. LifeWiki, 2010. augusztus 21. [2013. december 14-i dátummal az eredetiből archiválva]. (Hozzáférés: 2011. március 1.)
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Maze generation algorithm című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
További információk[szerkesztés]
- Gondolj a labirintusra: labirintusalgoritmusok (ezek és más labirintusgenerácló algoritmusok részletei)
- Jamis Buck: HTML 5 bemutató a labirintusgeneráló algoritmusok bemutatóival
- Labirintus generációs megjelenítés
- Prim algoritmusának Java-implementációja
- A DFS-labirintus létrehozási algoritmus megvalósítása több nyelven a Rosetta Code segítségével
- Armin Reichert: 34 labirintusalgoritmus Java 8-ban, demo alkalmazás segítségével
- CADforum: Labirintusgeneráló algoritmus a VisualLISP-ben
- Kódolási kihívás # 10.1: Labirintusgenerátor p5.js-vel - 1. rész: Labirintusgeneráló algoritmus JavaScript-ben a p5-rel
- Labirintusgenerátor: Charles Bond, COMPUTE! Magazin, 1981. december



