Kográf

A matematika, azon belül a gráfelmélet területén egy kográf (cograph), komplementer-redukálható gráf (complement-reducible graph) vagy P4-mentes gráf olyan gráf, ami a K1 egyetlen csúcsból álló gráfból kiindulva előállítható a komplementerképzés és diszjunkt unió gráfműveletek segítségével. Úgy is fogalmazhatunk, hogy a komplementer-redukálható gráfok családja a legkisebb gráfcsalád, ami tartalmazza a K1-et és a komplementerképzés, valamint a diszjunkt unió gráfműveleteire zárt.
A kográfokat az 1970-es évek során egymástól függetlenül több matematikus is leírta; a kográfokról szóló legkorábbi feljegyzések közé tartoznak: (Jung 1978), (Lerchs 1971), (Seinsche 1974) és (Sumner 1974). A szakirodalomban még a következő elnevezéseik is előfordulnak: D*-gráfok,[1] örökletes Dacey-gráfok (James C. Dacey Jr. ortomoduláris hálókon végzett kapcsolódó munkája után),[2] és 2-paritásgráfok.[3] Egyszerű, a diszjunkt unió és a komplementerképzés műveletein alapuló szerkezetük címkézett fa segítségével tömören ábrázolható, és hatékony algoritmusokkal oldhatók meg rajtuk olyan problémák (pl. a maximális klikk megkeresése), melyek általánosabb gráfosztályokon nehezebbek.
A kográfok speciális esetei közé tartoznak a teljes gráfok, a teljes páros gráfok, a klasztergráfok és a küszöbgráfok. Maguk a kográfok a távolság-örökletes gráfok, az összehasonlíthatósági gráfok és a perfekt gráfok speciális esetei.
Definíció
[szerkesztés]Rekurzív előállítása
[szerkesztés]Bármely komplementer-redukálható gráf előállítható a következő szabályok alapján:
- az egy csúcsból álló gráf kográf;
- ha kográf, akkor a komplementer gráfja, is az;
- ha és kográfok, akkor diszjunkt uniójuk, is az.
A komplementer-redukálható gráfok éppen azok a gráfok, melyek az egy csúcsból álló gráfból kiindulva, a fenti műveletek segítségével előállíthatók.[4] Alternatív megoldásként a komplementerképzés művelete helyett alkalmazható az összekapcsolás művelet, melynek során először a diszjunkt uniót képezzük, majd behúzunk minden lehetséges élt a és csúcsai között.
Egyéb karakterizációk
[szerkesztés]A komplementer-redukálható gráfok számos egyéb karakterizációja létezik. Néhány ezek közül:
- A kográfok azok a gráfok, melyek nem tartalmazzák feszített részgráfként a P4-et, azaz a 4 csúcs közötti (3 él hosszúságú) útgráfot (nincs bennük 3 él hosszú feszített út). Tehát egy gráf pontosan akkor kográf, ha bármely négy csúcsára, jelöljük őket -gyel, igaz, hogy ha és a gráf élei, akkor a és közül legalább egynek szintén élnek kell lennie.[4]
- A kográf olyan gráf, melynek feszített részgráfjaiban bármely maximális klikk bármely maximális független csúcshalmazt egyetlen csúcsban metsz.
- A kográf olyan gráf, melyben bármely nemtriviális feszített részgráf csúcsai közül legalább kettő ugyanabban a szomszédságban található.
- A kográf olyan gráf, melynek minden összefüggő feszített részgráfjának nem összefüggő a komplementere.
- A kográf olyan gráf, melynek minden összefüggő feszített részgráfjának legfeljebb 2 az átmérője.
- A kográf olyan gráf, melynek minden összefüggő komponense legfeljebb 2 átmérőjű távolság-örökletes gráf.
- A kográf olyan gráf, melynek klikkszélessége legfeljebb 2.[5]
- A kográf egy soros-párhuzamos részbenrendezés összehasonlíthatósági gráfja.[1]
- A kográf egy szétválasztható permutáció permutációgráfja.[6]
- A kográf olyan gráf, melynek minimális húrgráffá kiegészítései triviálisan perfekt gráfok.[7]
- A kográf örökletesen jól színezhető gráf, tehát olyan gráf, melynek minden feszített részgráfjának mohó színezése optimális.[8]
- A kográfok pontosan azok a gráfok, melyekben a csúcsok minden rendezése perfekt rendezés, mivel a P4 feszített részgráfok hiánya azt jelenti, hogy semmilyen sorrendben nincs akadálya a perfekt rendezésnek.
Kográf-fák
[szerkesztés]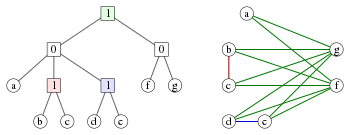
A kográfok egyedi fa-reprezentációval rendelkeznek.[9] Ez a reprezentáció a kográf-fa (cotree), ami egy olyan fa, aminek a belső csomópontjai a 0 és 1 számokkal vannak megcímkézve. Minden T kográf-fa meghatároz egy olyan G kográfot, melynek csúcsai megegyeznek a T leveleivel, és T bármely csomópontjából kiinduló részfa megfelel G-ben a csomópontból leszármazó levelek által a következő módon meghatározott feszített részgráfnak:
- Az egyetlen levélből álló részfa megfelel az egyetlen csúcsból álló feszített részgráfnak.
- A 0 címkéjű csomópont alatti részfa megfelel a csomópont gyerekei által meghatározott részgráfok uniójának.
- Az 1 címkéjű csomópont alatti részfa megfelel a csomópont gyerekei által meghatározott részgráfok összekapcsolásának (join művelet). Ezzel megegyezik, ha a részgráfoknak egyenként vesszük a komplementerét, ezek unióját képezzük, majd a végeredménynek újra a komplementerét vesszük.
A kográf-fa által meghatározott kográf leírásának egyenértékű módja a következő: két csúcs pontosan akkor van éllel összekötve, ha a nekik megfelelő levelek legközelebbi közös őse 1-gyel van címkézve. Megfordítva, minden kográf leírható ilyen módon egy kográf-fával. Ha megköveteljük, hogy bármely gyökér és levél közötti úton a címkék 0 és 1 között váltakozzanak, a reprezentáció egyértelmű.[4]
Példa
[szerkesztés]A következő példa bemutatja a kográf előállítását a hozzá tartozó kográf-fával együtt:
| Kográf | A kográf ábrázolása | A kográf-fa illusztrációja | Kográf-fa |
|---|---|---|---|
 |
|||
 |
 |
||
 |
 |
||
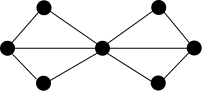 |
 |
Számítási jellemzőik
[szerkesztés]A kográfok lineáris időben felismerhetők, és létrehozható a kográf-fa reprezentáció, a következő módszerekkel: moduláris dekompozíció,[9] partíció finomítása, [10] lexikografikus szélességi bejárás (LexBFS) [11] vagy split dekompozíció.[12] Ha egyszer a kográf-fa reprezentáció elkészült, számos gráfprobléma megoldható a kográf-fán alulról fölfelé végzett egyszerű műveletek segítségével.
Például egy kográf maximális elemszámú klikkjének megkereséséhez alulról fölfelé ki kell számolni minden a kográf-fa minden részfájának megfelelő részgráf maximális elemszámú klikkjét. A 0-val címkézett csomópontok esetében a maximális elemszámú klikk megegyezik a gyermek csomópontok maximális klikkjével. Az 1-gyel címkézett csomópontok maximális elemszámú klikkje a gyermek csomópontok klikkjeinek uniója, mérete pedig a gyermekek klikkméreteinek összegével egyezik meg. Tehát a kográf-fa csomópontjaiban tárolt értékek váltakozva maximálásával és összegzésével kiszámítható a maximális elemszámú klikk mérete, a maximalizálás és unióképzés műveleteinek váltogatásával pedig meg is konstruálható a maximális elemszámú klikk. Hasonló alulról fölfelé történő számításokkal meghatározható a maximális elemszámú független csúcshalmaz, kromatikus szám, maximális klikkfedés[13] és a Hamilton-kör létezése, melyek a kográf-fa segítségével mind csak lineáris idejűek.[4] Mivel a kográfok klikkszélessége korlátos, a Courcelle-tétel felhasználásával a monadikus másodrendű gráflogika (MSO1) bármely tulajdonsága lineáris időben tesztelhető.[14]
Annak problémája, hogy adott gráf k csúcs és/vagyt él távolságon belül van-e egy kográftól, rögzített paraméter mellett kezelhető (fixed-parameter tractable).[15] Annak eldöntése, hogy egy gráf k él törlésével átalakítható-e kográffá O*(2,415k) időben,[16] hogy k él szerkesztésével átalakítható-e kográffá, O*(4,612k) időben eldönthető.[17] Ha egy gráf legnagyobb feszített részgráf-kográfja előállítható k csúcs törlésével, akkor O*(3,30k) időben meg is található.[16]
Két kográf pontosan akkor izomorf, ha kográf-fáik (kanonikus alakjukban, amikor szomszédos csúcsok nem kaphatják ugyanazt a címkét) izomorfak. Emiatt az ekvivalencia miatt lineáris időben eldönthető, hogy két kográf izomorf-e, csak meg kell konstruálni a kográf-fáikat és a címkézett fákra lineáris idejű izomorfizmus-tesztet futtatni.[4]
Ha H egy G kográf feszített részgráfja, akkor H maga is kográf; H kográf-fája előállítható a G kográf-fájából néhány levél eltávolításával, majd az egyetlen gyerekkel rendelkező csomópontok elnyomásával. A Kruskal-tételből következik, hogy a feszített részgráfnak levés relációja a kográfokon „jó előrendezés” (well-quasi-ordering).[18] Tehát ha a kográfok egy alosztálya (például a síkbarajzolható kográfok) zárt a feszített részgráf műveletre, akkor véges számú tiltott feszített részgráfja lehet. Számításilag ez azt jelenti, hogy az alosztályba tartozás adott esetben lineárisan tesztelhető, a gráf kográf-fáján a tiltott feszített részgráfok alulról fölfelé történő keresésével. Ha azonban mindkét kográf mérete variábilis, akkor annak vizsgálata, hogy az egyik a másiknak feszített részgráfja-e, NP-teljes probléma.[19]
A kográfok fontos szerepet játszanak a read-once függvényeket felismerő algoritmusokban.[20]
Leszámlálásuk
[szerkesztés]Az n csúcsú, összefüggő kográfok száma, n = 1, 2, 3-ra:
Az n > 1 esetekben ugyanennyi nem összefüggő kográf létezik, mivel mindegyiküknek pontosan egy komplementere összefüggő.
Kapcsolódó gráfcsaládok
[szerkesztés]Alosztályaik
[szerkesztés]Minden Kn teljes gráf kográf, melynek kográf-fája egy 1-címkéjű csomópontból és n levélből áll. Hasonlóan, minden Ka,b teljes páros gráf is kográf, melynek kográf-fája gyökerében 1-címkéjű csomópont van, két 0-címkéjű gyermekkel, melyek közül az egyik alatt a, a másik alatt b levél található. A Turán-gráf előállítható azonos méretű független csúcshalmazokon végzett összekapcsolás művelettel; ezért szintén kográf, melynek kográf-fája gyökerében 1-címkéjű csomópont van, mely alatt minden független csúcshalmazhoz egy-egy 0-címkéjű csomópont található.
A küszöbgráfok szintén kográfok. A küszöbgráf megkapható 1-1 olyan csúcs hozzáadásával, mely vagy az összes addigi csúcshoz kapcsolódik, vagy egyikhez sem; ezen műveletek mindegyike diszjunkt unió vagy összekapcsolás, melyekkel a kográf-fa előállítható. [21]
Bővebb halmazok
[szerkesztés]A kográfok azon karakterizációja, miszerint minden klikkjüknek és maximális független csúcshalmazuknak a metszete nem üres, az erősen perfekt gráf definíciójának erősebb változata; az erősen perfekt gráfokban elegendő, ha minden feszített részgráf tartalmaz olyan független csúcshalmazt, ami metszi a maximális klikkeket. A kográfokban az összes maximális független csúcshalmaz metszi az összes maximális klikket, ezért minden kográf erősen perfekt.[22]
Mivel a kográfok P4-mentesek, ezért perfekt rendezhetőek. Valójában a kográfok csúcsainak minden rendezése perfekt rendezés, amiből következik, hogy a maximális klikkeket és a minimális színezéseket lineáris időben lehet bennük keresni mohó algoritmussal, kográf-fára felbontás nélkül is.
Minden kográf egyben távolság-örökletes gráf, ami azt jelenti, hogy a kográf minden feszített útja egy legrövidebb út. A kográfok egyik karakterizációja szerint azok a távolság-örökletes gráfok, melyek minden komponensének legfeljebb kettő az átmérője. Minden kográf egyben egy soros-párhuzamos részbenrendezés hasonlítási gráfja is, ami úgy kapható meg, hogy a kográfot előállító diszjunkt unió és összekapcsolás műveletek helyett a részben rendezésen diszjunkt unió és lexikografikus összeg műveletet alkalmazunk. Mivel az erősen perfekt gráfok, perfekt rendezhető gráfok, távolság-örökletes gráfok és a hasonlítási gráfok mind perfektek, ezért a kográfok is mind perfekt gráfok.[21]
Jegyzetek
[szerkesztés]- ↑ a b Jung (1978).
- ↑ Sumner (1974).
- ↑ Burlet & Uhry (1984).
- ↑ a b c d e Corneil, Lerchs & Stewart Burlingham (1981).
- ↑ Courcelle & Olariu (2000).
- ↑ Bose, Buss & Lubiw (1998).
- ↑ Parra & Scheffler (1997).
- ↑ Christen & Selkow (1979).
- ↑ a b Corneil, Perl & Stewart (1985).
- ↑ Habib & Paul (2005).
- ↑ Bretscher et al. (2008).
- ↑ Gioan & Paul (2012).
- ↑ The maximum clique cover of a graph G = (V, E) is a set V' ⊆ V with the property that each maximum clique of G contains some vertex in the cover. – doi:10.1186/1471-2105-13-S10-S5
- ↑ Courcelle, Makowsky & Rotics (2000).
- ↑ Cai (1996).
- ↑ a b Nastos & Gao (2010).
- ↑ Liu et al. (2012).
- ↑ Damaschke (1990).
- ↑ Damaschke (1991).
- ↑ Golumbic & Gurvich (2011).
- ↑ a b Brandstädt, Le & Spinrad (1999).
- ↑ Berge & Duchet (1984).
Források
[szerkesztés]- Berge, C. & Duchet, P. (1984), "Strongly perfect graphs", Topics on Perfect Graphs, vol. 88, North-Holland Mathematics Studies, Amsterdam: North-Holland, pp. 57–61, DOI 10.1016/S0304-0208(08)72922-0.
- Bose, Prosenjit; Buss, Jonathan & Lubiw, Anna (1998), "Pattern matching for permutations", Information Processing Letters 65: 277–283, DOI 10.1016/S0020-0190(97)00209-3.
- Brandstädt, Andreas; Le, Van Bang & Spinrad, Jeremy P. (1999), Graph Classes: A Survey, SIAM Monographs on Discrete Mathematics and Applications, ISBN 978-0-89871-432-6.
- Burlet, M. & Uhry, J. P. (1984), "Parity Graphs", Topics on Perfect Graphs, vol. 21, Annals of Discrete Mathematics, pp. 253–277.
- Bretscher, A.; Corneil, D. G. & Habib, M. et al. (2008), "A simple Linear Time LexBFS Cograph Recognition Algorithm", SIAM Journal on Discrete Mathematics 22 (4): 1277–1296, DOI 10.1137/060664690.
- Cai, L. (1996), "Fixed-parameter tractability of graph modification problems for hereditary properties", Information Processing Letters 58 (4): 171–176, DOI 10.1016/0020-0190(96)00050-6.
- Christen, Claude A. & Selkow, Stanley M. (1979), "Some perfect coloring properties of graphs", Journal of Combinatorial Theory, Series B 27 (1): 49–59, DOI 10.1016/0095-8956(79)90067-4.
- Corneil, D. G.; Lerchs, H. & Stewart Burlingham, L. (1981), "Complement reducible graphs", Discrete Applied Mathematics 3 (3): 163–174, DOI 10.1016/0166-218X(81)90013-5.
- Corneil, D. G.; Perl, Y. & Stewart, L. K. (1985), "A linear recognition algorithm for cographs", SIAM Journal on Computing 14 (4): 926–934, DOI 10.1137/0214065.
- Courcelle, B.; Makowsky, J. A. & Rotics, U. (2000), "Linear time solvable optimization problems on graphs of bounded clique-width", Theory of Computing Systems 33 (2): 125–150, DOI 10.1007/s002249910009.
- Courcelle, B. & Olariu, S. (2000), "Upper bounds to the clique width of graphs", Discrete Applied Mathematics 101 (1–3): 77–144, DOI 10.1016/S0166-218X(99)00184-5.
- Damaschke, Peter (1990), "Induced subgraphs and well-quasi-ordering", Journal of Graph Theory 14 (4): 427–435, DOI 10.1002/jgt.3190140406.
- Damaschke, Peter (1991), "Induced subraph isomorphism for cographs is NP-complete", in Möhring, Rolf H., Graph-Theoretic Concepts in Computer Science: 16th International Workshop WG '90 Berlin, Germany, June 20–22, 1990, Proceedings, vol. 484, Lecture Notes in Computer Science, Springer-Verlag, pp. 72–78, DOI 10.1007/3-540-53832-1_32.
- Gioan, Emeric & Paul, Christophe (2012), "Split decomposition and graph-labelled trees: characterizations and fully dynamic algorithms for totally decomposable graphs", Discrete Applied Mathematics 160 (6): 708–733, DOI 10.1016/j.dam.2011.05.007.
- Golumbic, Martin C. & Gurvich, Vladimir (2011), "Read-once functions", in Crama, Yves & Hammer, Peter L., Boolean functions, vol. 142, Encyclopedia of Mathematics and its Applications, Cambridge University Press, Cambridge, pp. 519–560, ISBN 978-0-521-84751-3, doi:10.1017/CBO9780511852008.
- Habib, Michel & Paul, Christophe (2005), "A simple linear time algorithm for cograph recognition", Discrete Applied Mathematics 145 (2): 183–197, doi:10.1016/j.dam.2004.01.011, <http://www.lirmm.fr/~paul/Biblio/Postscript/DAM-cographs.pdf>.
- Jung, H. A. (1978), "On a class of posets and the corresponding comparability graphs", Journal of Combinatorial Theory, Series B 24 (2): 125–133, DOI 10.1016/0095-8956(78)90013-8.
- Lerchs, H. (1971), On cliques and kernels, Tech. Report, Dept. of Comp. Sci., Univ. of Toronto.
- Liu, Yunlong Liu; Wang, Jianxin & Guo, Jiong et al. (2012), "Complexity and parameterized algorithms for Cograph Editing", Theoretical Computer Science 461: 45–54, DOI 10.1016/j.tcs.2011.11.040.
- Nastos, James & Gao, Yong (2010), "A Novel Branching Strategy for Parameterized Graph Modification Problems", Lecture Notes in Computer Science 6509: 332–346.
- Parra, Andreas & Scheffler, Petra (1997), "Characterizations and algorithmic applications of chordal graph embeddings", Discrete Applied Mathematics 79 (1-3): 171–188, DOI 10.1016/S0166-218X(97)00041-3.
- Seinsche, D. (1974), "On a property of the class of n-colorable graphs", Journal of Combinatorial Theory, Series B 16 (2): 191–193, DOI 10.1016/0095-8956(74)90063-X.
- Sumner, D. P. (1974), "Dacey graphs", Journal of the Australian Mathematical Society 18 (4): 492–502, DOI 10.1017/S1446788700029232.




















