Bizonyíthatósági logika

A bizonyíthatósági logika a modális logika egyik fejezete, amelyben egy modális kijelentés olyan módon igaz, hogy bizonyítható egy formális rendszerben, pl. egy (intuicionista) logikában, Peano-aritmetikában, halmazelméletben. A bizonyíthatósági logika célja tehát egy adott formális rendszerben a bizonyíthatóság-fogalom megragadása. A bizonyíthatóságot e nyelvben egy $\scriptstyle {\Box }$ jellel szokás jelölni, és leggyakrabban „boksz”-nak szokás mondani.

A bizonyíthatósági logika megjelenését Kurt Gödel egy 1933-as cikkéhez szokás kapcsolni, melyben egy modális logika és az intuicionista logika kapcsolatával foglalkozik. A bizonyíthatósági logika leghíresebb eredményét, mely arról szólt, hogy a Peano-aritmetika bizonyíthatóság-fogalma pontosan megragadható egy modális logikával, Robert Martin Solovay publikálta 1976-ban.

Példák[szerkesztés]

Mikor egy formális rendszerben a bizonyíthatóság fogalmát egy modális logikával szándékozzuk megragadni, szükség van egy szótárra, ami a két nyelv formuláit valamilyen módon megfelelteti egymásnak. Fordításnak nevezzük és keretes zárójelekkel jelöljük majd azt a függvényt, amely a két nyelv formulái közt a kapcsolatot megteremti.

Az alábbiakban szerepel a két leghíresebb, fenti bevezetőben is említett fordításokkal egy-egy példa. Az első példában modális logikára, a másodikban modális logikából való fordításra szerepel példa, azonban mindkét fordítás fordított irányba is tökéletesen működik (ezen megállapítások bizonyításai számítanak a terület fő eredményeinek.)

Intuicionista logika[szerkesztés]

Az intuicionista logikánál az egyik alkalmas fordítás szerint, amely az ún. S4 modális logikába fordít, minden atomi mondat és negációjel elé egy $\scriptstyle {\Box }$ -ot kell írni, így pl. egy, a kizárt harmadik elvét képviselő formula a következő alakot ölti:

\scriptstyle {p\vee \lnot p\quad \rightsquigarrow \quad \Box p\vee \Box \lnot \Box p}

Szóban mondva a kapott modális formulát „ $\scriptstyle p$ állításnak rendelkezünk a bizonyításával, vagy a bizonyíthatóságának cáfolatával”.

A modális logikából ismert lehetséges világok szemantikája alapján S4-re a következő szemantika áll a rendelkezésünkre: A lehetséges világok különböző tudásállapotoknak felelnek meg, melyek egymással olyan módon kapcsolódnak össze, hogy az egyik tudásállapot információi kibővíthetők-e a másik tudásállapot információivá. Ez alapján ez az ún. alternatívareláció egy előrendezésnek felel meg, azaz

reflexív, azaz minden tudásállapot (triviális) bővítése a saját információinak
tranzitív, azaz ha egy $\scriptstyle {w_{1}}$ tudásállapot kibővíthető egy $\scriptstyle {w_{2}}$ -vé, ami pedig egy $\scriptstyle {w_{3}}$ -má, akkor $\scriptstyle {w_{1}}$ is kibővíthető $\scriptstyle {w_{3}}$ -má.

A bizonyíthatóság ide pedig úgy kapcsolódik, hogy, ha valamit bebizonyítottunk, akkor azt mindörökké tudni fogjuk; minden későbbi tudásállapotban ott lesz. Eszerint $\scriptstyle {\Box A}$ egy $\scriptstyle {w}$ tudásállapotban akkor és csak akkor szerepel, vagy más szóval igaz, ha minden későbbi, ebből kibővítve kapott tudásállapotban is igaz.

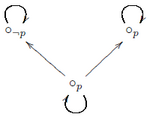
A fenti formula azonban a következő ábra (modális logikai modell) miatt hamis is lehet, így a kizárt harmadik törvényét képviselő formula nem logikai igazság – ami az intuicionista logikából valóban levezethetetlen. Ugyanis ha az alsó tudásállapotban helyezkedik el a $\scriptstyle \Box p\vee \Box \lnot \Box p$ formula, akkor ez valóban hamis lesz, mivel egyrészt $\scriptstyle \Box p$ valóban nem igaz, hiszen a bal oldali tudásállapotban hamis a $\scriptstyle {p}$ , másrészt pedig $\scriptstyle \Box \lnot \Box p$ sem igaz, mivel a jobb oldali világnak minden rákövetkezőjében (azaz önmagában) igaz a $\scriptstyle p$ .

A szemantika szemszögéből tehát azt mondhatjuk, hogy az S4 kalkulusnak két (adekvát) szemantikája is lehetséges, az egyik a Kripke-szemantika, a másik pedig a nulladrendű intuicionista logika.

Peano-aritmetika[szerkesztés]

A Peano-aritmetika egy fordítása úgy néz ki, hogy a Peano-aritmetikában szereplő azon $\scriptstyle {Bew}$ predikátumot, mely a levezethetőséget kódolja, írjuk át $\scriptstyle \Box$ -ra. Mivel $\scriptstyle {Bew}$ a Peano-aritmetikában lévő levezethetőségnek felel meg, így $\scriptstyle \Box$ rajta keresztül a bizonyíthatóságot ragadja majd meg.

A Peano-aritmetikára illeszkedő (Gödel és Löb után) GL modális logikában nézzük a következő formulát:

\scriptstyle {\Box \lnot \Box \bot \quad \rightsquigarrow \quad Lev(\ulcorner \lnot Lev(\ulcorner 0=1\urcorner )\urcorner )}

Ez a formula, ha a fordítás tényleg jó, nem lehet tétel. Azt fejezi ugyanis ki, hogy „levezethető, hogy nem bizonyítható az ellentmondás”, azaz hogy bizonyítható az aritmetika konzisztenciája – ennek azonban maga a második nemteljességi tétel állja útját.

A GL-ről tehát majd azt mondhatjuk, hogy két szemantika adható rá; az egyik a szokásos Kripke-szemantika, a másik pedig a Peano-aritmetika.

A kutatás két iránya[szerkesztés]

A bizonyíthatósági logika ötlete Gödeltől származik, amikor 1933-ban megfogalmazott egy fordítást a nulladrendű intuicionista kalkulus és C.I. Lewis S4 modális kalkulusa közt. Gödel ugyanakkor még ebben a cikkben leszögezte, hogy az S4-ben szereplő $\scriptstyle \Box$ nem jelentheti általában véve egy formális rendszerben a bizonyíthatóságot, mivel a kalkulusnak tételei olyan formulák, melyek ilyen módon interpretálva az aritmetikát tartalmazó formális rendszerekben ellent mondanának a Gödel-féle nemteljességi tételeknek. Ilyen például az S4-beli $\scriptstyle {\Box (\Box bot\rightarrow \bot )}$ formula. Mivel egy formális rendszerben bizonyítható $\scriptstyle {\top }$ , $\scriptstyle {\sim \Box \bot }$ is bizonyítható lenne, ami nem mást jelent, mint hogy nem bizonyítható az ellentmondás - ez pedig a konzisztenciát jelentené, ami az aritmetikát tartalmazó rendszerekben nem bizonyítható.

Innen indulva a bizonyíthatósági logikának két fő területe van:

Megadni a bizonyíthatóság logikáját, azaz megadni azt a modális logikát, amely egy adott formális rendszerben leírja a $\scriptstyle \exists xBew(x,y)$ bizonyíthatóságról szóló predikátumot. Ezt a $\scriptstyle Bew(x,y)$ predikátumot akkor tekintenénk igaznak, ha $\scriptstyle x$ bizonyítása lenne $\scriptstyle y$ -nak, ahol is egy Peano-aritmetikát tartalmazó formális rendszerben $\scriptstyle y$ lehetne a kérdéses formula Gödel-száma, $\scriptstyle x$ pedig a hozzá vezető bizonyítás (formulasorozat) Gödel-száma. Ebben az esetben tehát egy meglévő modellhez keresünk kalkulust.
Megadni a bizonyítások logikáját, azaz a meglévő, konstruktív bizonyításokat elviekben jól leíró S4 kalkulusra, és így az IPC kalkulusra egy bizonyításokkal kapcsolatos szemantikát.

A bizonyítások logikája[szerkesztés]

Modális logikák intuicionista logikára[szerkesztés]

S4[szerkesztés]

IPC lefordítása S4-re
$\scriptstyle {[p]}$	$\scriptstyle {\Box p}$
$\scriptstyle {[\lnot A]}$	$\scriptstyle {\Box \lnot [A]}$
$\scriptstyle {[A\rightarrow B]}$	$\scriptstyle {[A]\rightarrow [B]}$
$\scriptstyle {[A\vee B]}$	$\scriptstyle {[A]\vee [B]}$
$\scriptstyle {[A\land B]}$	$\scriptstyle {[A]\land [B]}$

Gödel használta először a modális operátort bizonyíthatósági interpretációban, mikor 1933-ban kimutatta az intuicionista logikáról, hogy lefordítható C. I. Lewis egyik modális kalkulusába – ez a rendszer S4 volt.^[1] Egy jó fordítás például az oldalt található (rekurzív) $\scriptstyle {[\cdot ]}$ függvény, melyet szokás Gödel-fordításnak is nevezni.^[2] Ez szemléletesen szólva annyit tesz, hogy minden atomi formula és negációjel elé elhelyez egy $\scriptstyle \Box$ jelet. Van azonban több lehetséges fordítás is, pl. hogy minden részformulát ellátunk egy $\scriptstyle \Box$ jellel.

S4 modelljei a reflexív és tranzitív keretstruktúrák (lásd: Modális logika). Itt a lehetséges világok episztemikus állapotokat jelölnek. A fordítás során pl. az intuicionista negáció szerepére a következőképpen lehet a S4 modális szemantikájának ismeretében rávilágítani:

$\scriptstyle \lnot A\quad \rightsquigarrow \quad \scriptstyle \Box \lnot A$ szemléletes jelentése: Innentől mindig tudjuk majd, hogy $\scriptstyle A$ hamis.

Nem az S4 modális kalkulus az egyetlen modális kalkulus, amelybe a nulladrendű intuicionista logikát be lehet ágyazni, azonban bizonyítható, hogy ez a leggyengébb ilyen kalkulus. A legerősebb ezek közül a Grz.

Grz[szerkesztés]

Ezt a modális kalkulust úgy kaphatjuk a K normális modális rendszerből, hogy egyetlen axiómaként az

Grz

\scriptstyle \Box (\Box (p\to \Box p)\rightarrow p)\rightarrow p

formulát vesszük fel. Ebből az axiómából levezethetők S4 axiómái, azaz $\scriptstyle \Box p\rightarrow p$ és $\scriptstyle \Box p\to \Box \Box p)\rightarrow p$ .

Grz Kripke modelljei azon keretstruktúrák lesznek, melyek reflexívek, tranzitívak, és nincsen bennük végtelen szigorúan felszálló ág. Ez utóbbi egy olyan elsőrendben nem definiálható tulajdonság, mely a következő egymással ekvivalens állításokat jelenti:

A világok halmazának bármely részhalmazában lesz egy olyan elem, amelynek csak önmaga a rákövetkezője.
Ha van olyan véletlen sorozat, hogy $\scriptstyle w_{1}Rw_{2}Rw_{3}R\dots$ , akkor ebben egy ponttól kezdve mindenhol ugyanaz a világ szerepel.

Ezekből már következik az (önmagában modálisan nem definiálható) antiszimmetria is, azaz Grz modelljei speciális parciális rendezések lesznek.

A bizonyíthatóság logikája[szerkesztés]

A Peano-aritmetika modális kalkulusai[szerkesztés]

GL[szerkesztés]

GL lefordítása PA-ra
$\scriptstyle {[p]}$	$\scriptstyle {p}$
$\scriptstyle {[\lnot A]}$	$\scriptstyle {\lnot [A]}$
$\scriptstyle {[A\rightarrow B]}$	$\scriptstyle {[A]\rightarrow [B]}$
$\scriptstyle {[A\vee B]}$	$\scriptstyle {[A]\vee [B]}$
$\scriptstyle {[A\land B]}$	$\scriptstyle {[A]\land [B]}$
$\scriptstyle {[\Box A]}$	$\scriptstyle {Lev\,(\ulcorner [A]\urcorner )}$

Az egyik legfontosabb bizonyíthatósági modális rendszer a GL rendszer (Gödel és Löb után) melyre a Kripke-féle (keretstruktúrás) szemantikán kívül egy alternatív szemantika is adható. Ez az alternatív – egyébként helyes és teljes – szemantika egy a Peano-aritmetika nyelvére való fordítás. A fordítás a $\scriptstyle {\Box }$ -okhoz a Gödel-számozást és a bizonyíthatósági predikátumot használja fel.

Bizonyíthatóság-predikátum

A $\scriptstyle {PA\vdash \sigma }$ jelölés azt jelenti, hogy a $\scriptstyle {\sigma }$ aritmetikai formula levezethető $\scriptstyle {PA}$ -ból. Erről Gödel munkássága óta tudjuk, hogy ennek egy árnyéka, vetülete megjelenik $\scriptstyle {PA}$ nyelvében magában is: Vezessük be először is a $\scriptstyle {\ulcorner \sigma \urcorner }$ függvényjelet. Ez minden formulához és formulasorozathoz hozzárendel egy számot (lásd: Gödel-számozás). Ezáltal a Peano-aritmetika képes lesz olyan formulákat levezetni, melyek a levezetéseiről 'szólnak'. Ezt követően bevezetünk majd egy predikátumot, $\scriptstyle {Biz}$ -t, amit a következőképpen definiálunk:

Ez a predikátum akkor és csak akkor legyen igaz, ha ez a $\scriptstyle {\sigma }$ aritmetikai formula Gödel-száma levezethető $\scriptstyle {PA}$ -ból

Azaz:

\scriptstyle {Lev\,(\ulcorner \sigma \urcorner )\quad \iff \quad PA\vdash \sigma }

Ekkor a Gödel-tétel értelmében a következő - modális formuláink konstrukciójához hasonló konstrukcióval bíró - formulákra bukkanhatunk beszédünkben, miközben $\scriptstyle {PA\vdash \sigma }$ -ról tettünk a fenti módszerrel megállapításokat.

Ha $\scriptstyle {PA\vdash \sigma }$ , akkor $\scriptstyle {PA\vdash Lev\,(\ulcorner \sigma \urcorner )}$ is.
$\scriptstyle {Lev\,(\ulcorner \sigma \rightarrow \tau \urcorner )\rightarrow (Lev\,(\ulcorner \sigma \urcorner )\rightarrow Lev\,(\ulcorner \tau \urcorner ))}$
$\scriptstyle {Lev\,(\ulcorner \sigma \urcorner )\rightarrow Lev\,(\ulcorner Lev\,(\ulcorner \sigma \urcorner )\urcorner )}$
$\scriptstyle {Lev\,(\ulcorner Lev\,(\ulcorner \sigma \urcorner )\rightarrow \sigma \urcorner )\rightarrow Lev(\ulcorner \sigma \urcorner })$

Azaz, a könnyebb áttekinthetőség érdekében a $\scriptstyle {Lev\,(\ulcorner \cdot \urcorner )}$ helyébe $\scriptstyle {\Box }$ -ot írva:

Modális generalizáció: Ha $\scriptstyle {PA\vdash A}$ , akkor $\scriptstyle {PA\vdash \Box A}$ is.
K: $\scriptstyle {\Box (A\rightarrow B)\rightarrow \Box A\rightarrow \Box B}$
tra : $\scriptstyle {\Box A\rightarrow \Box \Box A}$
Löb : $\scriptstyle {\Box (\Box A\rightarrow A)\rightarrow \Box A}$

Itt az első három jellemzőt tehát a modális generalizációt, K-t, tra-t (ami a K4 rendszert adja) szokás Hilbert–Bernays–Löb-féle levezethetőségi kritériumoknak is nevezni, mivel ezek olyan állítások, melyek egy természetes elvárást támasztanak a bizonyíthatósági predikátumunktól (és így a bizonyíthatósági modalitástól is).

Az utolsó formula Löb tételéből származik, mégpedig a következőképpen: Minden $\scriptstyle {PA}$ -beli formulának vannak ún. fix pontjai, azaz olyan $\scriptstyle {\sigma }$ mondatok, melyekre a diagonalizációs lemma alapján fennáll: $\scriptstyle {PA\,\vdash \,\sigma \,\,\leftrightarrow \,\,F\,(\ulcorner \sigma \urcorner )}$ . Mármost a $\scriptstyle {Lev}$ predikátum fixpontja ez alapján: $\scriptstyle {PA\,\vdash \,\sigma \,\,\leftrightarrow \,\,Lev\,(\ulcorner \sigma \urcorner )}$ . Az egyik irány az első (modális generalizálásnak megfelelő) állításból következik. Arra a kérdésre, hogy vajon a másik irány bizonyítható-e, Löb adott egy különös választ (és ez lenne Löb tétele): Ha $\scriptstyle {PA\,\vdash \,Lev\,(\ulcorner \sigma \urcorner )\,\,\rightarrow \,\,\sigma }$ , akkor $\scriptstyle {PA\,\vdash \,\sigma }$ .

Ez utóbbit $\scriptstyle {PA}$ nyelvére átírva megkapjuk a Löb formulának megfelelő számelméleti állítást:

Löb:

\scriptstyle {Lev\,(\ulcorner Lev\,(\ulcorner \sigma \urcorner )\rightarrow \sigma \urcorner )\rightarrow Lev(\ulcorner \sigma )\urcorner \quad }

,

Löb:

\scriptstyle {\quad \Box (\Box A\rightarrow A)\rightarrow \Box A}

A GL modális logika

A GL modális logikát úgy kapjuk, hogy a K normális modális logikához hozzávesszük az utolsó Löb formulát. Ebből már következni fog a tra formula, tehát axiómarendszerként az előbbi négy megállapítás fog szerepelni.

Modális szempontból az így kapott GL logika néhány érdekessége:^[3]

Az alternatívareláció irreflexív lesz.^[4]
A hozzá tartozó keretstruktúrák pontosan azok, amelyek tranzitívak és inverz jólfundáltak. Ez utóbbi a következő (ekvivalens kijelentéseket) jelenti:
- $\scriptstyle {R^{-1}}$ jólrendezett,
- nincsen $\scriptstyle {R}$ szerint felszálló végtelen lánc.
- nincsenek $\scriptstyle {w_{1},w_{2},w_{3}...}$ világok, hogy $\scriptstyle {...w_{3}Rw_{2}Rw_{1}}$
  $\scriptstyle {\forall P\exists x(Px\land \forall y(Py\rightarrow (\lnot x=y\rightarrow yRx)))}$
$\scriptstyle {\Box A\rightarrow A}$ nem tétele, de ez az előbbi tulajdonságból is következik.
Nincsenek $\scriptstyle {\Diamond A}$ formájú tételei. Mint például a $\scriptstyle {\lnot \Box \lnot \top }$ , azaz $\scriptstyle {\lnot \Box \bot }$ . Ez ugyanis olyasmit jelenthetne, hogy bizonyítható lenne, hogy a 0=1 állítás nem bizonyítható – ez pedig szó szerint az aritmetika ellentmondás-mentességének bizonyítása, ami a II. Gödel-tétel értelmében nem lehetséges.
$\scriptstyle {\top }$ tekintetében még a $\scriptstyle {\Box \Diamond \top }$ sem tétele GL-nek.
$\scriptstyle {\Box \bot \leftrightarrow \Box \Diamond \top }$ viszont tétel.
Viszont valahányszor tétele GL-nek egy $\scriptstyle {\Box A\rightarrow A}$ formula, annyiszor tétele $\scriptstyle {A}$ maga is. Ez Löb tételével cseng össze.

A GL kalkulus - Jobbra nyithatod ki a táblázatokat!

A GL kalkulus
Axiómák	Klasszikus	(A1)	$\scriptstyle {A\rightarrow (B\rightarrow A)}$
		(A2)	$\scriptstyle {(A\rightarrow (B\rightarrow C))\rightarrow ((A\rightarrow B)\rightarrow (A\rightarrow C))}$
		(A3)	$\scriptstyle {((\lnot A)\rightarrow (\lnot B))\rightarrow (B\rightarrow A)}$
	Modális	K	$\scriptstyle {\Box (A\rightarrow B)\rightarrow (\Box A\rightarrow \Box B)}$
	Modális	Löb	$\scriptstyle {\Box (\Box A\rightarrow A)\rightarrow \Box A}$
Levezetési szabályok:	Klasszikus	(MP)	$\scriptstyle {\frac {A,A\rightarrow B}{B}}$
Levezetési szabályok:	Modális	(MG)	$\scriptstyle {\frac {A}{\Box A}}$

GLS[szerkesztés]

Források[szerkesztés]

szerk.: Solomon Feferman: Collected Works (angol, német nyelven). Oxford: Oxford University Press (1986). ISBN 0-19-503964-5
George Boolos. The Logic of Provability. New York: Cambridge University Press (1993). ISBN 0-521-48325-5

Külső hivatkozások[szerkesztés]

Sergei N. Artemov, Lev. D. Beklemishev. Provability Logic (angol nyelven), 174. o.

Jegyzetek[szerkesztés]

↑ Solomon Feferman Kurt Gödel Collected Works, i. m. 1 kötet, 2 fejezet, 296. o.
↑ Szokás még használni a Gödel-Tarski-McKinsey fordítás elnevezést is.
↑ Boolos 1993 p. xvii.
↑ Az olyan keretstruktúra-osztály, amely pontosan az irreflexív keretstruktúrákat tartalmazza, modálisan definiálhatatlan. A GL azonban erősebb rendszer így lehetséges, hogy minden modellje irreflexív.

[1] Solomon Feferman Kurt Gödel Collected Works, i. m. 1 kötet, 2 fejezet, 296. o.

[2] Szokás még használni a Gödel-Tarski-McKinsey fordítás elnevezést is.

[3] Boolos 1993 p. xvii.

[4] Az olyan keretstruktúra-osztály, amely pontosan az irreflexív keretstruktúrákat tartalmazza, modálisan definiálhatatlan. A GL azonban erősebb rendszer így lehetséges, hogy minden modellje irreflexív.

[1]

[2]

[3]

[4]