„Kihajlás” változatai közötti eltérés
| [ellenőrzött változat] | [nem ellenőrzött változat] |
a →Tetmajer képlete: kisebb formai javítások, |
a →Euler képlete: correct final pattern |
||
| 7. sor: | 7. sor: | ||
[[Leonhard Euler]] [[1757]]-ben a meghatározta a kritikus törőerő nagyságát arra az esetre, ha a törőerő által okozott nyomófeszültség kisebb, mint a rúd anyagának [[folyáshatár]]a, más szóval, ha rugalmas kihajlás esete forog fenn. Ebben az esetben felírható a rugalmas szál [[differenciálegyenlet]]e: |
[[Leonhard Euler]] [[1757]]-ben a meghatározta a kritikus törőerő nagyságát arra az esetre, ha a törőerő által okozott nyomófeszültség kisebb, mint a rúd anyagának [[folyáshatár]]a, más szóval, ha rugalmas kihajlás esete forog fenn. Ebben az esetben felírható a rugalmas szál [[differenciálegyenlet]]e: |
||
:<math>\frac {d^2y}{dx^2} =-\frac{M}{ |
:<math>\frac {d^2y}{dx^2} =-\frac{M}{IE} </math>, |
||
ahol az ''x'' tengelyt a rúd tengelyében vesszük fel, [[Koordinátarendszer|origó]]jával a rúd egyik csuklós végpontjában (ahol a csukló miatt nyomaték nem ébredhet), az ''y'' tengely erre merőleges, ''M'' a rúd egy tetszőleges pontját terhelő hajlító [[nyomaték]], ''I |
ahol az ''x'' tengelyt a rúd tengelyében vesszük fel, [[Koordinátarendszer|origó]]jával a rúd egyik csuklós végpontjában (ahol a csukló miatt nyomaték nem ébredhet), az ''y'' tengely erre merőleges, ''M'' a rúd egy tetszőleges pontját terhelő hajlító [[nyomaték]], ''I'' a rúd keresztmetszetének legkisebb [[másodrendű nyomaték]]a, ''E'' pedig a rúd anyagának [[rugalmassági modulus]]a. Az ''M'' hajlítónyomaték az ''F<sub>t</sub>'' törőerő és az ''y'' kitérés szorzata: |
||
:<math>M=F_ty \,</math>. |
:<math>M=F_ty \,</math>. |
||
Végül, ha bevezetjük az |
Végül, ha bevezetjük az |
||
:<math>\alpha^2 =\frac{F_t}{ |
:<math>\alpha^2 =\frac{F_t}{IE} </math> |
||
jelölést, a [[differenciálegyenlet]] ilyen alakú lesz: |
jelölést, a [[differenciálegyenlet]] ilyen alakú lesz: |
||
:<math>y^{\prime\prime} + \alpha^2y = 0 </math>. |
:<math>y^{\prime\prime} + \alpha^2y = 0 </math>. |
||
| 22. sor: | 22. sor: | ||
Ez utóbbi nem triviális megoldásaiból gyakorlatilag az az érdekes eset, ha <math> \alpha l = \pi \frac{}{} </math>. |
Ez utóbbi nem triviális megoldásaiból gyakorlatilag az az érdekes eset, ha <math> \alpha l = \pi \frac{}{} </math>. |
||
Visszahelyettesítve az értékeket a kritikus törőerő értékét kapjuk: |
Visszahelyettesítve az értékeket a kritikus törőerő értékét kapjuk: |
||
:<math> F_t = \left ( \frac{\pi}{l} \right )^ |
:<math> F_t = \left ( \frac{\pi}{l} \right )^2IE </math>. |
||
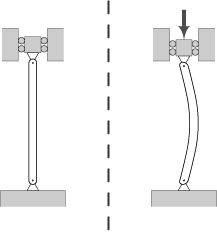
Ha a nyomott rúd nem csuklóval rendelkezik a végén, a differenciálegyenlet azonos lesz, csak a peremfeltételek lesznek eltérőek és ezek befolyásolják a törőerő nagyságát. Az alábbi ábra szerinti esetekre összefoglalóan a következő összefüggés írható: |
Ha a nyomott rúd nem csuklóval rendelkezik a végén, a differenciálegyenlet azonos lesz, csak a peremfeltételek lesznek eltérőek és ezek befolyásolják a törőerő nagyságát. Az alábbi ábra szerinti esetekre összefoglalóan a következő összefüggés írható: |
||
:<math> F_t = \left ( \frac{\pi}{ |
:<math> F_t = \left ( \frac{\pi}{l_{r}} \right )^2IE </math>, |
||
:<math>l_{r}=\mu{l}\,</math> |
|||
ahol μ a befogás fajtájától függő tényező, értéke az ábrán látható. |
ahol μ a befogás fajtájától függő tényező, értéke az ábrán látható. |
||
| 32. sor: | 34. sor: | ||
:<math>\sigma_t = \frac{F_t}{T} </math>, |
:<math>\sigma_t = \frac{F_t}{T} </math>, |
||
ahol ''T'' a keresztmetszet területe. A másodrendű nyomaték az ''i'' inerciasugárral is felírható: |
ahol ''T'' a keresztmetszet területe. A másodrendű nyomaték az ''i'' inerciasugárral is felírható: |
||
:<math> |
:<math>I = i^2 T \,</math>, |
||
és bevezetve a |
és bevezetve a |
||
:<math>\lambda = \frac{ |
:<math>\lambda = \frac{l_{r}}{i} </math>, |
||
karcsúságot, az Euler-képlet a törőfeszültségre így írható: |
karcsúságot, az Euler-képlet a törőfeszültségre így írható: |
||
:<math> \sigma_t = \left ( \frac{\pi}{ |
:<math> \sigma_t = \left ( \frac{\pi}{\lambda} \right )^2E </math>, |
||
== Tetmajer képlete == |
== Tetmajer képlete == |
||
A lap 2010. január 22., 18:22-kori változata
A kihajlás az a mechanikai jelenség, amely keresztmetszetéhez képest hosszú egyenes rúd tengelyébe eső, megfelelően nagy nyomóerő hatására bekövetkezik.
Ha a nyomóerő kicsi, a rúd kissé összenyomódik, de egyenes marad. Ha a nyomóerőt növeljük, akkor egy bizonyos kritikus értéknél a rúd elgörbül, kihajlik és eltörik. Azt az erőt, amelynél a rúd eltörik, kritikus törőerőnek nevezik. Kis nyomóerő esetén a nyomott rúd stabil egyensúlyi helyzetben van, mivel ha a rúdra merőleges kis erővel terheljük, a rúd meggörbül, de a merőleges erő megszüntetésével visszatér eredeti helyzetébe. A törőerő elérésekor a kis oldalirányú erő okozta alakváltozás az erő megszüntetése után is megmarad. Ekkor a rúd közömbös (indifferens) egyensúlyi helyzetben van. Ha a rúd terhelése a kritikus törőerőnél nagyobb, a kitérés addig fokozódik, amíg a rúd eltörik, vagyis a rúd állapota instabil.
Euler képlete
Leonhard Euler 1757-ben a meghatározta a kritikus törőerő nagyságát arra az esetre, ha a törőerő által okozott nyomófeszültség kisebb, mint a rúd anyagának folyáshatára, más szóval, ha rugalmas kihajlás esete forog fenn. Ebben az esetben felírható a rugalmas szál differenciálegyenlete:
- ,
ahol az x tengelyt a rúd tengelyében vesszük fel, origójával a rúd egyik csuklós végpontjában (ahol a csukló miatt nyomaték nem ébredhet), az y tengely erre merőleges, M a rúd egy tetszőleges pontját terhelő hajlító nyomaték, I a rúd keresztmetszetének legkisebb másodrendű nyomatéka, E pedig a rúd anyagának rugalmassági modulusa. Az M hajlítónyomaték az Ft törőerő és az y kitérés szorzata:
- .
Végül, ha bevezetjük az
jelölést, a differenciálegyenlet ilyen alakú lesz:
- .
Ennek az egyenletnek az általános megoldása:
- ,
ahol A és B a peremfeltételektől függ. Mivel az l hosszúságú rúd mindkét végén csuklós megfogású,
- és , így
- és
- .
Ez utóbbi nem triviális megoldásaiból gyakorlatilag az az érdekes eset, ha . Visszahelyettesítve az értékeket a kritikus törőerő értékét kapjuk:
- .
Ha a nyomott rúd nem csuklóval rendelkezik a végén, a differenciálegyenlet azonos lesz, csak a peremfeltételek lesznek eltérőek és ezek befolyásolják a törőerő nagyságát. Az alábbi ábra szerinti esetekre összefoglalóan a következő összefüggés írható:
- ,
ahol μ a befogás fajtájától függő tényező, értéke az ábrán látható.
A gyakorlatban a törést okozó σt nyomófeszültséget szokás számolni:
- ,
ahol T a keresztmetszet területe. A másodrendű nyomaték az i inerciasugárral is felírható:
- ,
és bevezetve a
- ,
karcsúságot, az Euler-képlet a törőfeszültségre így írható:
- ,
Tetmajer képlete

A törőfeszültség csak akkor számítható a fenti összefüggés segítségével, ha az az arányossági határnál kisebb. Ebben a tartományban rugalmas kihajlásról beszélünk. Ha a törőfeszültséget a karcsúság függvényében ábrázoljuk, eredményül egy másodfokú hiperbolát, az úgynevezett Euler-hiperbolát kapjuk, amely azonban csak az arányossági határig érvényes. A folyáshatár a törőfeszültség felső határát jelenti. A folyáshatár és az arányossági határ között plasztikus kihajlásról beszélünk. Ebben a tartományban a magyar származású Tetmajer Lajos kísérletei szerint a λ - σt diagramban egy egyenessel ábrázolhatók. Ezek szerint:
- ,
| Anyag | Szakítószilárdság MPa |
III. szakasz λ<λF | II. szakasz λF <λ< λe | I. szakasz λ>λe σt MPa | ||
|---|---|---|---|---|---|---|
| σt = σF MPa |
λf | σt = a - bλ MPa |
λe | |||
| Szénacél | 370 | 240 | 60 | 308-1,14λ | 105 | |
| 480 | 310 | 60 | 467-1,62λ | 100 | ||
| 520 | 360 | 60 | 589-3,82λ | 100 | ||
| Ötvözött acél | 650 | 420 | 22 | 470-2,30λ | 86 | |
| Dúralumínium | 420 | - | 0 | 380-2,20λ | 50 | |
| Öntöttvas | - | - | 5 | 776-12λ+0,053λ² | 80 | |
| Fenyőfa | - | - | 0 | 30-0,2λ | 100 | |
| Tölgyfa | - | - | 0 | 37,5-0,25λ | 100 | |
Forrás
- Muttnyánszky Ádám: Szilárdságtan. Műszaki könyvkiadó, Budapest, 1981. ISBN 963 10 359 13
- Pattantyús Gépész- és Villamosmérnökök Kézikönyve 2. kötet. Műszaki Könyvkiadó, Budapest, 1961.


























