Vonalfelület
|
|
Ez a szócikk vagy szakasz lektorálásra, tartalmi javításokra szorul. |
| Ezt a szócikket némileg át kellene dolgozni a wiki jelölőnyelv szabályainak figyelembevételével, hogy megfeleljen a Wikipédia alapvető stilisztikai és formai követelményeinek. |
A geometriában az a felület vonalfelület, amelynek minden pontján át húzhatunk egy olyan egyenest, ami az adott felületen halad végig.
Ilyen például a sík, a hengerpalást vagy a kúpfelület.
A vonalfelületet úgy képzelhetjük el, mint egy egyenes térben történő mozgatásának lenyomatát. Pl. kúpfelületet úgy képezhetünk ezzel a módszerrel, hogy egy egyenes egyik pontját rögzítjük, egy másik pontját pedig körbevezetjük egy körön.
Kétszer vonalazott felület[szerkesztés]
Kétszer vonalazott a felület, ha minden pontján át két különböző rajta fekvő egyenes húzható.
Ilyen például a sík (ez az egyetlen n-szeresen vonalazott felület, ha n >= 3), a hiperbolikus paraboloid (nyeregfelület) vagy a hiperbolikus hiperboloid.
Paraméterezés[szerkesztés]
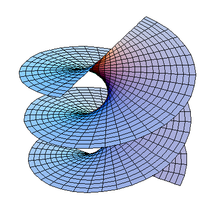
A mozgó egyenes leírható az
egyenlettel, ahol a felület általános pontja, a görbén végigfutó pont, az egységgömbön, ami végigköveti a görbét.
Például, ha
akkor olyan felületet kapunk, amely tartalmazza a Möbius-szalagot.
A vonalfelület paraméterezhető úgy is, hogy , ahol és a felület két, egymást nem metsző görbéje. Például, ha és két kitérő egyenesen fut végig konstans sebességgel, akkor hiperbolikus paraboloidot, vagy egyköpenyű hiperboloidot kapunk.
Síkba teríthető felület[szerkesztés]
Egy felület síkba teríthető, ha nyújtás vagy összenyomás nélkül síkba teríthető. Ha egy síkba teríthető felület teljes tér a háromdimenziós térben, akkor vonalfelület, így például a gömb nem teríthető síkba. Fordítva viszont nem áll a dolog. A henger- és kúpfelület például síkba teríthető, de az egyköpenyű hiperboloid már nem. Általánosabban, ha a háromdimenziós térben egy felület síkba teríthető, akkor van olyan vonalfelület, ami tartalmazza. Négy dimenzióban viszont léteznek olyan síkba teríthető felületek, amik nem vonalfelületek.[1]
Algebrai geometria[szerkesztés]

Az algebrai geometriában a vonalfelületeket olyan projektív felületekből származtatják, amik minden pontjára illeszkedik egy egyenes, ami teljes egészében a felület része. Ez a feltétel definícióként is szolgál.
Az építészetben[szerkesztés]
A kétszeresen vonalazott felületek lehetőséget adnak arra, hogy egyenes építőelemekből görbült felszínt hozzanak létre. Így épülnek hiperbolikus paraboloid alakú nyeregtetők, egyköpenyű hiperboloid alakú hűtőtornyok és szeméttárolók.
-
Cooling Hiperbolikus tornyok a Didcot Power Stationnál, Nagy-Britanniában; a felszín kétszeresen vonalazott.
-
Hiperboloid alakú Kobe Port Torony, Kobe, Japán.
-
The gridshell of Shukhov Tower in Moscow, whose sections are doubly ruled.
-
Kúp alakú szalmakalap.
Jegyzetek[szerkesztés]
- ↑ Hilbert & Cohn-Vossen 1952, pp. 341-342.
Források[szerkesztés]
- Barth, Wolf P.; Hulek, Klaus; Peters, Chris A.M.; Van de Ven, Antonius (2004), Compact Complex Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge., 4, Springer-Verlag, Berlin, MR2030225, ISBN 978-3-540-00832-3
- Beauville, Arnaud (1996), Complex algebraic surfaces, London Mathematical Society Student Texts, 34 (2nd ed.), Cambridge University Press, MR1406314, ISBN 978-0-521-49510-3; 978-0-521-49842-5
- Edge, W. L. (1931), The Theory of Ruled Surfaces, Cambridge, University Press . Review: Bull. Amer. Math. Soc. 37 (1931), 791-793, doi:10.1090/S0002-9904-1931-05248-4
- Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8 .
- Iskovskikh, V.A. (2001), "Ruled surface", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104















