Thévenin-tétel

A villamosságtanban Thévenin tétele a hálózatanalízisben használt tétel, ami azt mondja ki, hogy két pólus felől, bármely, csak áram- illetve feszültséggenerátorokat és ellenállásokat tartalmazó (tehát lineáris) villamos hálózat helyettesíthető egy valós feszültséggenerátorral (egy ideális feszültséggenerátor és egy vele sorba kapcsolt ellenállás).[1] A tétel nemcsak ellenállásokra, hanem egyetlen frekvenciát tartalmazó váltakozó áramú rendszerek esetén impedanciákra is alkalmazható. A tételt tulajdonképpen Hermann von Helmholtz német mérnök fedezte fel 1853-ban, de Léon Charles Thévenin francia telegráfmérnök nevéhez kötjük, aki 1883-ban fedezte fel újból.
A Thévenin-tétel számolása[szerkesztés]
- A Thévenin-helyettesítésben a generátor feszültsége megegyezik az eredeti hálózat kijelölt kapcsain mérhető üresjárási feszültséggel (a vizsgált kapcsok közti feszültség, ha nincs terhelő ellenállás bekötve)
- Az ellenállás nagysága megegyezik a dezaktivizált hálózat eredő ellenállásával (az "AB" oldal felől nézve), ilyenkor a szuperpozíció-tételhez hasonlóan a (független) feszültséggenerátorokat rövidzárnak, az áramgenerátorokat szakadásnak kell tekinteni.
A Thévenin-tétel alkalmazható egyen- és váltóáramú hálózatokra is, azonban váltóáramú hálózatnál figyelembe kell venni az induktív és a kapacitív tagokat is, tehát komplex módon kell számolni.
Példa:
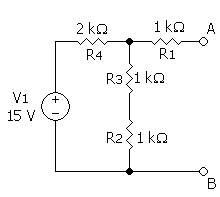 |
 |
 |
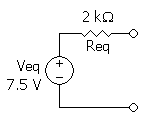 |
1. lépés:
2. lépés:
Konvertálás Norton-tétellé[szerkesztés]
A Thévenin-féle helyettesítő áramkör konvertálható Norton-helyettesítéssé, a következő módszerrel:
Források[szerkesztés]
- Angol wikipédia
- Budapesti Műszaki Főiskola – Villamosságtan I. tankönyv (Óbuda)




![{\displaystyle R_{\mathrm {b} }=R_{1}+\left[\left(R_{2}+R_{3}\right)\|R_{4}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bd8468fc87fe26f92623bc05c9dcec38c95b5b8)
![{\displaystyle =1\,\mathrm {k} \Omega +\left[\left(1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \right)\|2\,\mathrm {k} \Omega \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88305e6af8f126727745786cc21ac95e058b11e0)



