Racionális törtfüggvény

A racionális törtfüggvény a valós számok halmazának olyan önmagára való leképezése, amelyben a hozzárendelést két polinom hányadosával adjuk meg:

$y={\frac {P_{m}(x)}{Q_{n}(x)}}={\frac {a_{m}x^{m}+a_{m-1}x^{m-1}+...+a_{1}x+a_{0}}{b_{n}x^{n}+b_{n-1}x^{n-1}+...+b_{1}x+b_{0}}}$ .

A függvény két polinomfüggvény, vagyis racionális egészfüggvény hányadosa. Az együtthatók lehetnek racionális, valós vagy komplex számok, az egyetlen kikötés, hogy $Q_{n}(x)$ nem lehet nulla, emiatt nem lehet az azonosan nulla polinom.

A leképezés értelmezési tartománya azokból a valós számokból áll, amelyekre $Q_{n}(x)$ nem nulla.

Típusai

Ha a $Q_{n}$ polinom foka nulla, azaz konstans, akkor a függvény polinomfüggvény, vagyis racionális egészfüggvény.

Egyébként, ha a nevező foka nagyobb, akkor valódi racionális törtfüggvényről van szó.

Ha ez nem teljesül, akkor a racionális törtfüggvény nem valódi. Polinomosztással egy polinom és egy racionális törtfüggvény összegeként ábrázolható.

A táblázat mutat néhány példát a számláló különböző $z$ fokaira és a nevező különböző $n$ fokaira:

Példa	Alternatív írásmód	z =	n =	Függvénytípus
$f\colon x\mapsto {\frac {3x^{3}-4x+5}{2}}$	$f\colon x\mapsto {\frac {3}{2}}x^{3}-2x+{\frac {5}{2}}$	3	0	racionális egészfüggvény
$f\colon x\mapsto {\frac {2x-1}{x^{2}+1}}$		1	2	valódi racionális törtfüggvény
$f\colon x\mapsto {\frac {(x-1)^{2}\cdot (x+2)}{x\cdot (2-3x^{2})}}$	$f\colon x\mapsto {\frac {x^{3}-3x+2}{2x-3x^{3}}}$	3	3	nem valódi racionális törtfüggvény
$f\colon x\mapsto x+1+{\frac {1}{x-1}}$	$f\colon x\mapsto {\frac {x^{2}}{x-1}}$	2	1	nem valódi racionális törtfüggvény

Tulajdonságai

Mivel $Q_{n}(x)$-nek legfeljebb n nullhelye van, a függvény értelmezési tartománya legfeljebb n+1 nyílt intervallum uniója. Ezeken a nyílt intervallumokon a függvény folytonos és akárhányszor differenciálható. Az összefüggő zárt résztartományokon integrálható. A függvény grafikonja általában egy vagy több aszimptotával rendelkezik.

Fokszám, rendszám

Az m illetve n fokszámú polinomokkal definiált törtfüggvényeket (m/n)-edfokúnak nevezzük, s a grafikonjuk r rendszámát az egyenletük implicit alakjában szereplő legmagasabb fokszámmal adjuk meg:

${\begin{cases}y.Q_{n}(x)=P_{m}(x)\\y.a_{m}x^{m}+\dots =a_{n}x^{n}+\dots \end{cases}}$

${\begin{cases}r=m+1,~(m+1\geq n)\\r=n,~(m+1<n)\end{cases}}$

Fontosabb törtfüggvények

Fordított arányosság

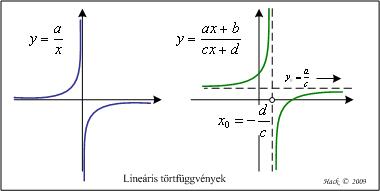
A görbe hiperbola (kúpszelet), explicit illetve implicit egyenlete:

$y={\frac {a}{x}}~;~xy=a$

(Az ábrán $a<0$ együtthatójú görbe, aszimptotái a koordináta-rendszer tengelyei.)

Lineáris törtfüggvény

A függvény és grafikonja az egyenes arányosság transzformáltja.

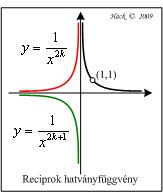
Reciprok hatványfüggvény

Pontosabban: negatív egész kitevőjű hatványfüggvény. Grafikonja hiperbolikus típusú görbe. Páros kitevő esetén a két ága az Y tengelyre, páratlan kitevő esetén az origóra szimmetrikus.

Reciprok polinomfüggvény

Az n-edfokú polinom reciprokaként megadott racionális törtfüggvény, melynek grafikonja a nevezőtől függően változatos alakú és számú nyílt görbeívből áll. A görbe rendszáma: r = n+1.

Az ábrán az $y={\frac {1}{ax^{2}+bx+c}}$ explicit alakban adott harmadrendű görbe látható. (Ennek speciális esete az Agnesi-féle görbe)

Aszimptotika

A racionális törtfüggvényeknek szakadásuk van a nevező gyökeinél. Emellett még a végtelenben vett viselkedés is kérdéses.

A végtelenben vett viselkedés szempontjából a nevező és számláló foka döntő fontossággal bír. A szakasz további részében $z$ a számláló, $n$ a nevező fokszáma. Ha $x\to \infty$, akkor $f(x)$

• tart $\operatorname {sgn} \left({\tfrac {a_{z}}{b_{n}}}\right)\cdot \infty$-hez, hogyha $z>n$, ahol $\operatorname {sgn}$ a szignumfüggvény.
• tart ${\tfrac {a_{z}}{b_{n}}}$-hez, ha $z=n$ (az aszimptota párhuzamos az $x$-tengellyel),
• tart $0$-hoz (az $x$-tengely vízszintes aszimptota), ha $z<n$.

Ha $x\to -\infty$, akkor a második és a harmadik esetben ugyanaz a határérték, mint $x\to \infty$ esetén. A többi eset:

• Ha $z-n$ páros, akkor az érték ugyanaz, mint $x\to \infty$ esetén.
• Ha $z-n$ páratlan, akkor az előjel ellentettje az $x\to \infty$ értékének.

Ahogy majd később írjuk, polinomosztással a függvény felbontható egy polinom és egy valódi racionális törtfüggvény összegére. A polinom aszimptotikus görbét ad. A $z=n+1$ speciális esetben ferde aszimptota adódik. Az aszimptotikus görbe vizsgálatával az $x\to \pm \infty$ viselkedése egyszerűbben elemezhető.

Példák:

• Az $f\colon x\mapsto {\frac {2x-1}{x^{2}+1}}$ lineáris törtfüggvény esetén a számláló foka $z=1$ és a nevező foka $n=2$, így az $x\to \pm \infty$ határérték $0$.
• Az $f\colon x\mapsto {\frac {x^{3}-3x+2}{2x-3x^{3}}}$ racionális törtfüggvény számlálójának foka $z=3$, nevezőjének foka $n=3$; a főegyütthatók $a_{3}=1$ und $b_{3}=-3$, tehát adódik az aszimptota egyenlete: $y=-{\frac {1}{3}}$.
• Az $f\colon x\mapsto {\frac {x^{2}}{x-1}}$ racionális törtfüggvény számlálójának foka $z=2$, nevezőjének foka $n=1$; az $a_{2}=1$ és $b_{1}=1$ főegyütthatókkal adódik, hogy

$f(x)\to \operatorname {sgn} \left({\tfrac {1}{1}}\right)\cdot \infty =+\infty$, ha $x\to \infty$. Mivel $z-n=1$ páratlan, azért $x\to -\infty$ határértékének előjele az előző ellentettje. A függvény írható úgy is, mint $f\colon x\mapsto x+1+{\frac {1}{x-1}}$, a ferde aszimptota egyenlete $y=x+1$, amivel az előbbi értékek könnyebben adódnak.

Diszkusszió

Az $f={p \over q}\colon x\mapsto {\frac {p(x)}{q(x)}}$ függvényterm grafikonjának elemzésére a következő diszkusszió végezhető.

Szimmetria

Mivel szakadásai a $q$ gyökeiben vannak, a gyökök száma pedig véges, azért az $f$ periodikusságáról nem lehet szó.

Egy polinomfüggvény akkor páros vagy páratlan, ha minden kitevője páros vagy páratlan. Ha a számláló és a nevező típusa is ilyen, akkor az $f$ racionális törtfüggvény páros vagy páratlan. Nevezetesen:

• Ha $p$ és $q$ egyszerre páros vagy páratlan, akkor a racionális törtfüggvény páros.
• Ha $p$ és $q$ egyike páros, másika páratlan, akkor $f$ páratlan.

Egyéb esetben nehéz $f$ szimmetriáját meghatározni.

Példák:

• Az $f(x)={\frac {2x^{3}-3x}{x^{2}+1}}$ függvény szimmetrikus az origóra, mivel $p$ páratlan és $q$ páros, a függvény páratlan.
• Az $f\colon x\mapsto {\frac {x^{5}-x^{3}}{x^{3}+x}}$ függvény szimmetrikus az y tengelyre, mivel $p$ és$q$ is páratlan, így a hányados függvény páros. Kiemelve egy x-et a számlálóból és a nevezőből, egyszerűsíthetjük a függvényt az $f(x)={\frac {x^{4}-x^{2}}{x^{2}+1}}*{\frac {x}{x}}$. Mivel itt $p$ és $q$ páros, azért a hányados függvény is páros.
• Az $f(x)={\frac {x}{x-1}}$ függvényről nem lehet szimmetriát megállapítani az alakja alapján, de megmutatható, hogy szimmetrikus a P(1, 1) pontra, ugyanis:

  $f(1+x)-1={\frac {1+x}{(1+x)-1}}-1={\frac {1+x}{x}}-{\frac {x}{x}}={\frac {1}{x}}$ és

  $1-f(1-x)=1-{\frac {1-x}{(1-x)-1}}={\frac {x}{x}}+{\frac {1-x}{x}}={\frac {1}{x}}$.

Eszerint elvégezve az átalakításokat $f(1+x)-1=1-f(1-x)$, tehát szimmetrikus az szimmetrikus a P(1, 1) pontra. Egy alternatív módszer, hogy belátjuk, hogy a függvény megkapható $g\colon x\mapsto {\frac {1}{x}}$-ből eltolással, azaz 1-gyel x irányba, és 1-gyel y irányba.

Értelmezési tartomány, nevezetes pontok

A racionális törtfüggvény nincs értelmezve a $q$ polinom gyökeiben. Nullhelyei azok a helyek, melyek gyökei $p$-nek, de nem gyökei $q$-nak.

Speciális esetben az $a\in \mathbb {R}$ valós szám mind a számlálónak, mind a nevezőnek gyöke. Polinomosztással kiemelhető egy vagy több $x-a$ tényező mind a számlálóból, mind a nevezőből. Hogy hányszor, azt a gyök multiplicitásának nevezik.

• Ha a nevezőben nagyobb a multiplicitás, akkor a hely pólushely, és a nevezőbeli multiplicitás a pólushely multiplicitása.
• Különben a szakadás megszüntethető.

Példák:

• Az $f\colon x\mapsto {\frac {x-1}{(2x-4)^{2}}}$ függvény értelmezési tartománya $\mathbb {D} =\mathbb {R} \setminus \{2\}$, mivel a $q\colon x\mapsto (2x-4)^{2}$ nevezőnek nullhelye $x=2$. A függvénynek nullhelye van $x=1$-ben, mivel ez a $p\colon x\mapsto x-1$ számlálónak egy olyan nullhelye, ami nem gyöke a nevezőnek. $x=2$ kétszeres pólus.
• Az $f\colon x\mapsto {\frac {x^{2}-x}{x^{2}-1}}$ függvény értelmezési tartománya $\mathbb {D} _{f}=\mathbb {R} \setminus \{\pm 1\}$. Itt azonban 1 a számláló és a nevező közös gyöke. Kiemelve az $(x-1)$ tényezőt, adódik, hogy $f\colon x\mapsto {\frac {x\cdot (x-1)}{(x+1)\cdot (x-1)}}$. Innen $x=-1$ egyszeres pólus, $x=1$ megszüntethető szakadás, $x=0$ nullhely. Az $x=1$ helyen nincs nullhely, mivel itt a függvény nincs értelmezve. $f$ folytonos folytatására ${\tilde {f}}(x)={\frac {x}{x+1}}$ és $\mathbb {D} _{\tilde {f}}=\mathbb {R} \setminus \{-1\}$.

Aszimptoták

Polinomosztással kapjuk a függvény $p=g\cdot q+r$ alakját, ahol $g$ és $r$ polinomok, és $r$ fokszáma kisebb, mint $q$ fokszáma. Az $f={p \over q}=g+{r \over q}$ függvény aszimptotikus viselkedését a $g$ polinom határozza meg. A polinomosztást csak a harmadik és a negyedik esethez érdemes elvégezni.

1. $z<n$ → az x-tengely aszimptota: $g(x)=0$
2. $z=n$ → függőleges aszimptota: $g(x)={\frac {a_{z}}{b_{n}}}$
3. $z=n+1$ → ferde aszimptota: $g(x)=mx+c\,;m\neq 0$ (a 4-es speciális esete)
4. $z>n+1$ → racionális egészfüggvény mint közelítőfüggvény, lásd approximáció

Derivált

A racionális törtfüggvények deriválásához általában a hányadosszabályt lehet használni, habár gyakran a láncszabály is hasznos lehet, például ha a nevező egy kéttagú összeg hatványa. A deriválás előtt előnyös elvégezni a polinomosztást, a számláló és a nevező közös tagjainak kiemelését egy külön tényezőbe, hogy a függvény alakja minél egyszerűbb legyen.

Példák:

• Az $f\colon x\mapsto {\frac {2x-1}{(x^{2}+1)^{2}}}$ függvény esetén érdemes a láncszabályt is használni, mivel a nevezőben binom hatványa szerepel. A láncszabállyal a $q$ nevező deriváltja:

  $q'(x)=2(x^{2}+1)\cdot 2x=4x(x^{2}+1)$,

így a teljes függvény deriváltja

$f'(x)={\frac {2\cdot (x^{2}+1)^{2}-(2x-1)\cdot 4x(x^{2}+1)}{(x^{2}+1)^{4}}}$.

A számlálóban kiemelhetünk egy $(x^{2}+1)$ tényezőt:

$f'(x)={\frac {2\cdot (x^{2}+1)-(2x-1)\cdot 4x}{(x^{2}+1)^{3}}}{\frac {(x^{2}+1)}{(x^{2}+1)}}$.

• Az $f(x)={\frac {x^{4}+x^{3}-7x^{2}-12x-4}{3x^{3}+12x^{2}+12x}}$ függvény polinomosztással

  $f(x)={\frac {1}{3}}x-1+{\frac {x^{2}-4}{3x^{3}+12x^{2}+12x}}$

alakra hozható, ahonnan leolvasható a ferde aszimptota egyenlete:

$y={\frac {1}{3}}x-1$.

A számláló és a nevező tényezőkre bontása:

$f(x)={\frac {1}{3}}x-1+{\frac {(x+2)(x-2)}{3x(x+2)^{2}}}$,

felismerhető és kiemelhető mindkét helyen egy $(x+2)$ tényező. A deriválásra előkészített alak:

$f(x)={\frac {1}{3}}x-1+{\frac {x-2}{3x^{2}+6x}}{\frac {(x+2)}{(x+2)}}$;

az egyszerűség kedvéért ebből az

$f(x)={\frac {1}{3}}x-1+{\frac {x-2}{3x^{2}+6x}}$;

tényezőt fogjuk deriválni. A hányadosszabállyal

$f'(x)={\frac {1}{3}}+{\frac {1\cdot (3x^{2}+6x)-(x-2)\cdot (6x+6)}{(3x^{2}+6x)^{2}}}={\frac {1}{3}}+{\frac {-3x^{2}+12x+12}{(3x^{2}+6x)^{2}}}={\frac {1}{3}}+{\frac {-x^{2}+4x+4}{3x^{2}(x+2)^{2}}}$.

A szélsőértékek kereséséhez a deriváltat újra beszorozzuk az elhagyott tényezővel:

$f'(x)={\frac {x^{2}(x+2)^{2}-x^{2}+4x+4}{3x^{2}(x+2)^{2}}}={\frac {x^{4}+4x^{3}+3x^{2}+4x+4}{3x^{2}(x+2)^{2}}}$.

Primitív függvény

A racionális egészfüggvényekkel szemben a racionális törtfüggvényeknek gyakran viszonylag nehéz meghatározni a primitív függvényét. A racionális törtfüggvény alakja szerint a következő összefüggéseket lehet használni, amihez általában a megfelelő alakra kell hozni:

$\int {\frac {1}{mx+a}}dx={\frac {1}{m}}\cdot \ln(mx+a)+C$ ha $m,a\in \mathbb {R} ,m\neq 0$

$\int {\frac {1}{(mx+a)^{n}}}dx={\frac {1}{m}}\cdot {\frac {-1}{n-1}}\cdot {\frac {1}{(mx+a)^{n-1}}}+C$ ha $m,a\in \mathbb {R} ,m\neq 0,n\in \mathbb {N} \setminus \{0;1\}$

$\int {\frac {1}{x^{2}+1}}dx=\arctan(x)+C$ vagy $=-{\rm {arccot(x)+C}}$

$\int {\frac {1}{x^{2}-1}}dx=\operatorname {artanh} (x)+C={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)$ ha $|x|<1$

$\int {\frac {1}{x^{2}-1}}dx=\operatorname {arcoth} (x)+C={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)$ ha $|x|>1$

$\int {\frac {u'(x)}{u(x)}}dx=\ln |u(x)|+C$ ha $u(x)\neq 0$

Szükség lehet a parciális törtekre bontásra is. Példák:

• Keressük az $f(x)={\frac {5x-1}{3x+2}}$ függvény primitív függvényét. Polinomosztással:

  $f(x)={\frac {5}{3}}-{\frac {13}{9x+6}}$.

Az első szabály alkalmazásával a primitív függvény:

$F(x)={\frac {5}{3}}x-{\frac {13}{9}}\ln(9x+6)$.

• Keressük az $f(x)={\frac {x^{2}+1}{x^{2}-1}}$ függvény primitív függvényét, ha $x$ abszolútértéke legfeljebb 0,5. Polinomosztással

  $f(x)=1+{\frac {2}{x^{2}-1}}$.

A negyedik szabállyal:

$F(x)=x+2\cdot \operatorname {artanh} (x)$.

• Keressük az $f(x)={\frac {x+2}{x^{2}+4x+5}}$ függvény primitív függvényét. A függvény írható úgy is, mint

  $f(x)={\frac {1}{2}}{\frac {2x+4}{x^{2}+4x+5}}={\frac {1}{2}}{\frac {u'(x)}{u(x)}}$, ahol $u(x)=x^{2}+4x+5$.

Az utolsó szabály primitív függvénye:

$F(x)={\frac {1}{2}}\ln(x^{2}+4x+5)$.

• Az $f(x)={\frac {1}{x^{2}+2x+2}}$ függvény primitív függvénye az $y=x+1$ helyettesítéssel határozható meg, miután a nevezőt teljes négyzetté alakítottuk:

  ${\begin{aligned}\int {\frac {1}{x^{2}+2x+2}}dx&=\int {\frac {1}{(x+1)^{2}+1}}dx=\int {\frac {1}{y^{2}+1}}dy\\&=\arctan(y)+C=\arctan(x+1)+C\end{aligned}}$

• Az $f(x)={\frac {1}{x^{2}-x-6}}$ primitív függvénye parciális törtekre bontással kapható a kiemelések után:

  ${\begin{aligned}\int {\frac {1}{x^{2}-x-6}}dx&=\int {\frac {1}{(x-3)(x+2)}}dx=\int {\frac {1}{5}}\left({\frac {1}{x-3}}-{\frac {1}{x+2}}\right)dx\\&={\frac {1}{5}}\left(\ln(x-3)-\ln(x+2)\right)+C={\frac {1}{5}}\ln \left({\frac {x-3}{x+2}}\right)+C\end{aligned}}$

Alkalmazások

A természettudományokban és a technikában számos alkalmazásuk van a racionális törtfüggvényeknek:

• A legegyszerűbb példa a fordított arányosság, két mennyiség szorzata állandó. Példák:

• Rögzített út megtételéhez szükséges idő és sebesség.
• Adott mennyiségű oldott anyag koncentrációja fordítottan arányos az oldószer térfogatával.
• Adott erő esetén a gyorsított test tömege és gyorsulása.
• Egy síkkondenzátor $C$ elektromos kapacitása a lemezek közötti $d$ távolság függvényében:

$C(d)=\epsilon _{0}\epsilon _{r}{\tfrac {A}{d}}$,

ahol $A$ a lemezek felülete, $\epsilon _{0}$ a vákuum permittivitása, és $\epsilon _{r}$ a permittivitás.

• A fizika több területén is előkerül az $f(x;y)={\tfrac {xy}{x\pm y}}$ függvény a harmonikus középpel összefüggően. Ha az egyiket paraméternek tekintjük vagy adottnak vesszük, akkor a másik racionális törtfüggvénye adódik. KÉt másik függvény reciprokainak összegének reciprokáról van szó.

• Az optikában egy lencse $f$ gyújtótávolsága a tárgy $t$ és a kép $k$ távolságágából számítható: $f(t;k)={\tfrac {tk}{t+k}}$; átrendezve hasonló képlet adódik, de összeadás helyett kivonással.
• Párhuzamos kapcsolás esetén két ellenállás, $R_{1}$ és $R_{2}$ együttes ellenállása: $R={\tfrac {R_{1}R_{2}}{R_{1}+R_{2}}}$. Hasonló teljesül két sorosan kapcsolt kondenzátor kapacitására.
• A mechanikában ha két rugót egymás után függesztünk, és rugóállandójuk $D_{1}$ és $D_{2}$, akkor az együttes rugóállandó $D={\tfrac {D_{1}D_{2}}{D_{1}+D_{2}}}$.
• Feszültségelosztó esetén egy $R$ ellenálláson eső $U$ feszültség $U(R)={\tfrac {U_{0}R}{R+R'}}$, ahol $U_{0}$ az elosztandó feszültség és $R'$ a másik ellenállás.
• Egy $R$ ellenállású fogyasztó által leadott $P$ teljesítményére adódik, hogy $P(R)={\tfrac {U^{2}R}{(R+R_{i})^{2}}}$, ahol $U$ feszültség és $R_{i}$ a feszültségforrás belső ellenállása. A legnagyobb lehetséges teljesítmény: $R=R_{i}$.
• Egy nem túl rövid $L$ induktivitású tekercsre az $r$ sugárral összefüggésben teljesül a következő: $L(r)={\tfrac {\mu _{0}N^{2}\pi r^{2}}{l+r/1,1}}$, ahol $l$ a tekercs hossza, $N$ a menetek száma, $\mu _{0}$ a mágneses mező konstansa.
• Egy Atwood-féle gép esetén az $a$ gyorsulás a következőképpen függ $m$ és $M$ tömegektől: $a={\tfrac {m}{2M+m}}\cdot g$; $a$ tekinthető $m$ vagy $M$ racionális törtfüggvényének.

• A geometria is felvethet olyan kérdéseket, amelyekre racionális törtfüggvény adja a választ: Egy test egy $l$, $2r$, és $r$ élű téglatest és egy erre illesztett $l$ magasságú, $r$ sugarú félhenger egyesítése. Adott térfogat esetén a felszín: $A(r)={\tfrac {(\pi +4)r^{3}+2V}{r}}$.

Polinomok hányadosteste

Az absztrakt algebrában a polinomok hányadosteste hasonlóan áll elő polinomokból. Egy $K$ test fölötti $n$ változós polinomgyűrű hányadostestéről van szó absztrakt értelemben.

A racionális törtfüggvények szoros kapcsolatban állnak a polinomok gyűrűjének hányadostestével, de a két fogalom nem azonos. Például a

$p(x)={\frac {x-1}{x^{2}-1}}$

és a

$q(x)={\frac {1}{x+1}}$

kifejezések mint a valós együtthatós polinomok hányadostestének elemei egyenlőek, mivel ott $x^{2}-1$ osztható $x-1$-gyel, és a hányados $x+1$. De ha $p(x)$-et és $q(x)$-et mint racionális törtfüggvényeket tekintjük, akkor nem egyenlőek, hiszen $q(x)$ értelmezhető az $x=1$ helyen, $p(x)$ viszont nem.

Véges test fölött a különbségtétel még egyszerűbb: $\mathbb {F} _{p}$ (maradékosztályok teste modulo egyp prímszám) fölött definiált hányadostestben ${\tfrac {1}{X^{p}-X}}$ jóldefiniált racionális függvénye $X$-nek, habár szűkebb értelemben véve nem függvény, mivel sehol sem értelmezhető.

Ugyanis behelyettesítve $x\in \mathbb {F} _{p}$ elemeit, kapjuk, hogy ${\tfrac {1}{x^{p}-x}}$, ami nem értelmezhető, hiszen $x^{p}-x$ a kis Fermat-tétel miatt azonosan nulla. Végtelen test fölött ugyanez nem fordulhat elő, csak viszonylag kevés helyen nincs egy racionális törtfüggvény értelmezve. A Zariski-topológia szerint azok a helyek, ahol a függvény nincs értelmezve, Zariski-zárt halmazt alkotnak, és az értelmezési tartomány lezártja a teljes halmaz.

Legyen $V$ varietás, amit az $f_{1},\dotsc ,f_{m}\in k\left[x_{1},\dotsc ,x_{n}\right]$ polinomok definiálnak. Azaz

$V=\{x\in \mathbb {A} ^{n}\mid f(x)=0{\text{ minden }}f\in S\}$ esetén. Vagyis

$I(V)=\{f\in k[x_{1},\dotsc ,x_{n}]\mid f(x)=0{\text{ ha }}x\in V\}.$

Az egfész függvények gyűrűje $k[x_{1},\dotsc ,x_{n}]/I(V)$. A racionális függvények teste ennek hányadosteste.

Általánosabb a racionális leképezések fogalma, azaz a kvázi-projektív varietásoké. A racionális függvények egy varietás $\mathbb {A} ^{1}$-be menő racionális leképezéseinek speciális esetei.

Források

A Wikimédia Commons tartalmaz Racionális törtfüggvény témájú médiaállományokat.

• Rationale Funktionen - Ein Digitales Lehrbuch © 2000 - 2001 by Henning Koch

Fordítás

Ez a szócikk részben vagy egészben a Rationale Funktion című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Irodalom

• Bronstein – Szemengyajev: Matematikai zsebkönyv. Műszaki könyvkiadó, Budapest, 1987. ISBN 963 1053091
• Dr. Hack & all.: Négyjegyű függvénytáblázatok,…(Nemzeti Tankönyvkiadó, 2004) ISBN 978-963-19-5703-7
• Reiman István: Matematika (Műszaki Könyvkiadó, 1992)
• Reinhardt, F. – Soeder, H.: SH atlasz-Matematika (Springer-Verlag, 1993)
• Sain Márton: Matematikatörténeti ABC (Nemzeti Tankönyvkiadó - Typotex, 1993)
• Szász Pál: A differenciál- és integrálszámítás elemei (Közoktatásügyi Kiadóvállalat, 1951)
• Pattantyús Gépész- és Villamosmérnökök Kézikönyve 1. kötet. Műszaki Könyvkiadó, Budapest, 1961.