Létraparadoxon

A létraparadoxon egy gondolatkísérlet a speciális relativitáselmélet témakörében.

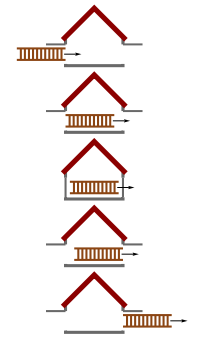
A létraparadoxon esetében egy létrát kell behelyezni egy garázsba, mely rövidebb, mint a létra. A létra nagy sebességgel vízszintesen mozog, és ezért hosszkontrakción megy keresztül, melynek eredményeként befér egy jóval kisebb garázsba.

Másrészt annak a megfigyelőnek a szemszögéből, aki a létrával mozog együtt, a garázs az az objektum, ami mozog, és a garázs hossza rövidül meg, ezért nem képes a létrát befogadni. Ez egy nyilvánvaló paradoxon. A relativitáselméletben az egyidejűség relatív, és így a létra mindkét esetben befér a garázsba.

A paradoxon

A létra és a garázs

A probléma ott kezdődik, hogy van egy létra és a szóban forgó garázs, mely túl rövid egy létrának. A relativitáselmélet hosszkontrakció-tétele következtében a létra alkalmas lesz arra, hogy beférjen a garázsba, ha az eléggé nagy sebességgel mozog befelé.

Mind a létrának, mind a garázsnak megvan a saját inerciarendszere (vonatkoztatási rendszere). A garázs vonatkoztatási rendszeréből tekintve, a létra relatív sebességgel mozog, és így a létra hosszkontrakciót szenved. Mivel szimmetrikus a rendszer, fordítva is igaz: a létra vonatkoztatási rendszeréből tekintve a garázs mozog relatív sebességgel, és így a garázs szenved hosszkontrakciót, így aztán a garázs kisebb lesz, és a létra nem fog beférni.

• 
  A mozgó létra hosszkontrakciója
• 
  A garázs hosszkontrakciója

A relatív egyidejűség

• 
  A garázs szemszögéből nézve: a megrövidült létra mozgása
• 
  A létra szemszögéből nézve: a megrövidült garázs és a létra

A nyilvánvaló paradoxonra a megoldás abban a tényben keresendő, hogy amit az egyik megfigyelő egyidejűnek tekint, az nem felel meg annak, amit a másik megfigyelő tekint egyidejűnek (relatív egyidejűség).

Világosabban áttekinthető a probléma, ha a garázs két kapuval rendelkezik, ahol az egyik lengő kapu befogadja a bejövő létrát, majd a hátsó kapu kinyílik, melyen a létra kijuthat. A garázs perspektívájából a megrövidült létra elég rövid ahhoz, hogy teljesen beférjen a garázsba. Amikor a létra bent van teljesen a garázsban, a bemeneti és a hátsó kapu is zárva van egyidejűleg. Mivel a létra még mindig mozog egy jelentős sebességgel, a bemeneti és a hátsó kapu egy időben újra kinyílik, és kiengedi a létrát.

A létra perspektívájából a hátsó (jobb oldali) kapu záródik be és nyílik ki, aztán miután a garázs elhalad a létra mellett, a bemeneti kapu (bal oldali) záródik be és nyílik ki.

A Minkowski-diagram: a létraparadoxon ábrázolása. A garázs világoskék színű, a létra világospiros. A diagram a garázs nyugalmi rendszerét mutatja, x-szel és t–vel jelölve a garázs tér- és időtengelyét. A létra rendszere azé a megfigyelőé, aki a létra elején ül, az x’ és t’-vel jelölve a létra tér- és időtengelyét. Az x és az x’ 5 láb hosszú a saját rendszereikben, és a t valamint t’ 5ns.

Ezt a helyzetet a Minkowski-diagram mutatja. A diagram a garázs nyugalmi inerciarendszerében van. A függőleges világoskékre satírozott sáv mutatja a garázs téridejét. A világosvörös sáv a létra téridejét mutatja. Az x és t a garázs tér- és időtengelye, míg a x′ és t′ a létra tér- és időtengelyei. A létra $v=c{\sqrt {1/2}}$ sebességgel mozog a pozitív x irányban, ezért $\gamma ={\sqrt {2}}$ (a létra szemszögéből a sebessége x' irányban hasonló.

Mivel a fény sebessége igen közeli az egy láb/ns (nanoszekundum) értékhez, ezt az egységet használjuk a továbbiakban, azaz: $c\approx 1{\mbox{ft/ns}}$. A garázs elég kisméretű, G=10 láb hosszú, míg a létra hossza L=12 láb. A garázs inerciarendszerében a létra eleje $t_{A}=G/v\approx 14.14{\mbox{ ns}}$ időpontban éri el a garázs hátsó kapuját (ha $t_{D}=t_{O}=0$-t választjuk referenciapontnak). Ez látható az A eseménynél a diagramban.

A garázs x tengelyével párhuzamos összes vonal egyidejű a garázsban lévő megfigyelő számára, így a sötétkék „AB” vonal az, amit a garázsban lévő megfigyelő lát a létra „A” eseménye idején. A létra a garázsban van. A létrán ülő megfigyelő azonban a sötétpiros „AC” vonalat látja. A létra vége kint van a garázsból.

Megoldás

A megrövidült létra befér a megrövidült garázsba

A megoldás az egyidejűség relativitásában rejlik. A paradoxont tekintve, amikor a létra belép a garázsba és bent van, akkor vagy folytatja az útját kifelé, vagy megáll. Amikor a létra teljesen megáll, akkor a garázs inerciarendszerébe gyorsul be. A garázs inerciarendszeréből, a létra minden része egyidejűleg teljesen megáll, és így minden résznek egyidejűleg kell gyorsulnia. A létra inerciarendszeréből nézve a garázs mozog, és ahhoz, hogy megálljon, a létrának kell gyorsulnia a garázs inerciarendszerébe. A létra minden része nem tud egyidejűleg gyorsulni, az egyidejűség relativitása miatt. Az történik, hogy a létra minden egyes része szekvenciálisan gyorsul, az elejétől a végéig, egészen addig, amíg a létra vége fel nem gyorsul, és a garázsba nem ér; ennek eredményeként a létra inerciarendszeréből nézve az első részek szekvenciális rövidülést szenvednek, egészen addig, amíg a teljes létra bent nem lesz a garázsban.

Minkowski-diagram 2.

A Minkowski diagram 2. azt az esetet mutatja, amikor a létra egész hosszában megáll, a garázs inerciarendszerében egyidejűleg. Amikor ez megtörténik, a garázs rendszere a létrát mint AB-t látja, de a létra rendszere a létrát mint AC látja. Amikor a létra hátsó része belép a garázs D pontján, még nem érzi az elejének a gyorsuló hatását. Ebben az időpontban annak, aki nyugalomban van a létra hátsó részét tekintve, a létra eleje az E ponton lesz, és ezért a létrát DE–ként látja. A létra rendszerében ez a hossz nem egyenlő a CA-val, ami a létra maradék hossza a lassulás előtt.

Kapcsolódó szócikkek

• Ikerparadoxon
• Bell űrhajósparadoxona
• Relativitáselmélet
• Általános relativitáselmélet
• Speciális relativitáselmélet
• Hendrik Lorentz
• Hosszkontrakció
• Idődilatáció
• Relativisztikus tömeg
• Részecskefizika
• Born-koordináták
• Ehrenfest-paradoxon
• Lorentz-transzformáció
• Michelson–Morley-kísérlet
• Hermann Minkowski
• Az egyidejűség relativitása

További információk

• http://math.ucr.edu/~jdp/Relativity/TwinParadox.html
• http://www.einsteins-theory-of-relativity-4engineers.com/ladder-paradox.html