Kitérés

A geometriában két térelem kitérő, ha nem metszik egymást, és nem párhuzamosak. A hiperbolikus síkgeometriában szokták az ultraparalel egyeneseket kitérőnek nevezni. Az euklideszi geometriában kitérő egyenesek csak legalább három dimenzióban vannak. Egyszerű példa egy szabályos tetraéder szemközti élpárjai. A projektív három-, vagy magasabb dimenziós térben is vannak kitérő egyenesek. A legalább három, páratlan dimenziójú véges projektív terek befedhetők kitérő egyenesekkel, vagyis minden ponton át a befedés pontosan egy egyenese megy át.

Két egyenes kitérő voltának belátásához elég azt belátni, hogy az egyenesek irányvektorai és az egyik egyenes egy pontját a másik egy pontjára toló eltolásvektorok egyike lineárisan független. Ekvivalensen, nincs sík, ami mindkét egyenest tartalmazza.

Bővebben[szerkesztés]

Egy kitérő egyenespár mindkét egyenesét egy pontpár határozza meg. Mivel az egyenesek nincsenek egy síkban, ezért ezek a pontok egy nem elfajuló tetraéder csúcsai. Megfordítva, egy nem nulla térfogatú tetraéder szemben fekvő élpárjai kitérők. Tehát az (a,b) és a (c,d) pontpárok által meghatározott egyenesek kitérő volta megállapítható a pontok által alkotott tetraéder térfogatának kiszámításával: ha a V = |det(a−b, b−c, c−d)|/6. Ha ez a mennyiség nem nulla, akkor az egyenesek kitérők.

Az egyenletes eloszlás szerint egy kockában választott két pontpár majdnem mindig kitérő egyenest határoz meg, mivel nulla annak a valószínűsége, hogy a negyedik pont az első három által meghatározott síkba essen; ugyanis a sík kockába eső részének térfogata nulla. Hasonlóan, a tér egy párhuzamos vagy metsző egyenespárjának kis mértékű elmozdulása is kitérő egyeneseket eredményez. A legalább háromdimenziós térben két egyenes egymáshoz viszonyított helyzete általános esetben kitérő; a metszés vagy a párhuzamosság speciális esetnek tekinthető.

A kitérő egyenesek távolsága[szerkesztés]

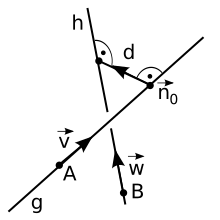
Minden kitérő egyenespárhoz van egy mindkettőre merőleges egyenes, ami mindkettőt metszi. Az ezzel vett metszéspontok távolsága a kitérő egyenesek távolsága.

Adva legyen a két kitérő egyenes, g és h rendre az A és B tartópontokkal, vagyis az ${\vec {a}}={\overrightarrow {OA}},\;{\vec {b}}={\overrightarrow {OB}}$ támaszvektorokkal, és a ${\vec {v}}$ és ${\vec {w}}$ irányvektorokkal. Ekkor az egyenesek egyenleteinek paraméteres alakja

g:{\vec {x}}={\vec {a}}+r{\vec {v}}

h:{\vec {x}}={\vec {b}}+s{\vec {w}}\ \ \,r,s\in \mathbb {R}

ahol ${\vec {a}},\,{\vec {b}},\,{\vec {v}},\,{\vec {w}}\in \mathbb {R} ^{3}$ és az ${\vec {a}}-{\vec {b}},\,{\vec {v}},\,{\vec {w}}$ vektoroknak lineárisan függetleneknek kell lenniük.

A közös ${\vec {n}}$ normálvektor mindkét normálvektorra, ${\vec {v}}$ -re és ${\vec {w}}$ -re is merőleges, ezért vektoriális szorzással számítható:

{\vec {n}}={\vec {v}}\times {\vec {w}}

lenormálva:

{\vec {n}}_{0}={\frac {{\vec {v}}\times {\vec {w}}}{|{\vec {v}}\times {\vec {w}}|}}

.

A távolság a normálvektoron levő támaszpontok összekötő vektorának merőleges vetítésével számítható. Ehhez le kell normálni a normálvektort. Ezzel tehát a kitérő egyenesek távolsága

d(g,h)=|({\vec {a}}-{\vec {b}})\cdot {\vec {n}}_{0}|.

Determinánsokkal[szerkesztés]

Az egyenesek egyenletei

g:{\vec {x}}=\left({\begin{smallmatrix}a_{1}\\[0.7ex]a_{2}\\[0.7ex]a_{3}\end{smallmatrix}}\right)+r\left({\begin{smallmatrix}v_{1}\\[0.7ex]v_{2}\\[0.7ex]v_{3}\end{smallmatrix}}\right)

h:{\vec {x}}=\left({\begin{smallmatrix}b_{1}\\[0.7ex]b_{2}\\[0.7ex]b_{3}\end{smallmatrix}}\right)+s\left({\begin{smallmatrix}w_{1}\\[0.7ex]w_{2}\\[0.7ex]w_{3}\end{smallmatrix}}\right)\ \ \,r,s\in \mathbb {R} .

A kitérő egyenesek távolsága determinánsokkal felírva:

d(g,h)={\frac {\left|\det {\begin{pmatrix}a_{1}-b_{1}&a_{2}-b_{2}&a_{3}-b_{3}\\v_{1}&v_{2}&v_{3}\\w_{1}&w_{2}&w_{3}\end{pmatrix}}\right|}{\sqrt {{\begin{vmatrix}v_{2}&v_{3}\\w_{2}&w_{3}\end{vmatrix}}^{2}+{\begin{vmatrix}v_{3}&v_{1}\\w_{3}&w_{1}\end{vmatrix}}^{2}+{\begin{vmatrix}v_{1}&v_{2}\\w_{1}&w_{2}\end{vmatrix}}^{2}}}}.

A talppontok meghatározása[szerkesztés]

Az F_h talppont meghatározásához szükség van egy E segédsíkra. Az A pont a hipersíkban fekszik, és a segédsíkot a ${\vec {v}}$ és az ${\vec {n}}$ vektorok feszítik ki.

E:{\vec {x}}={\vec {a}}+r{\vec {v}}+t{\vec {n}}\ \ ,r,t\in \mathbb {R}

, ahol az

{\vec {n}}

normálvektorra:

{\vec {n}}={\vec {v}}\times {\vec {w}}

.

E és h metszéspontja éppen az F_h talppont. Hasonlóan adódik F_gaz $E':{\vec {x}}={\vec {b}}+s{\vec {w}}+t{\vec {n}}\ \ \,s,t\in \mathbb {R}$ segédsíkkal és annak g-vel vett metszéspontjával.

A módszerhez nem kell kiszámítani az egyenesek távolságát.

Konfigurációk[szerkesztés]

A kitérő egyenesek által alkotott konfigurációkban minden egyenespár kitérő. Két konfiguráció izotopikus, ha az egyik folytonos mozgással átvihető a másikba, miközben minden egyenespár végig kitérő marad. Háromnál magasabb dimenzióban könnyen belátható, hogy minden, azonos elemszámú konfiguráció izotopikus. Három dimenzióban viszont több azonos elemszámú konfiguráció is van, ha az elemszám legalább három. (Viro & Viro 1990). A háromdimenziós valós euklideszi térben az n egyenest tartalmazó konfigurációk száma n = 1-től kezdve:

1, 1, 2, 3, 7, 19, 74, ... (A110887 sorozat az OEIS-ben)

A regulusok a projektív terek ismert kitérő egyenesekből álló konfigurációi, amelyek a befedésekben is szerepet kapnak.

Vonalazott felületek[szerkesztés]

Ha egy egyenes egy másik, hozzá kitérő, de rá nem merőleges egyenes körül forog, akkor egy egyköpenyű hiperboloid felszínt súrol. Az egyenes forgás közbeni helyzetei egy vonalazott felületet határoznak meg, amin egy másik, a forgástengelyhez kitérő egyenessereg is megtalálható, amelynek szöge megegyezik a forgó egyenesével, de ellenkező irányú.

Affin transzformációval elliptikus keresztmetszetű elliptikus hiperboloidokhoz jutunk. A harmadik fajta kitérő egyenesseregeket tartalmazó vonalazott felület a hiperbolikus paraboloid, ami szintén két kitérő egyenessereget tartalmaz. A valós háromdimenziós euklideszi geometriában bármely kitérő egyeneshármas meghatároz egy vonalazott felületet, aminek típusa e három típus közül kerül ki.

Véges projektív terekben a hasonló módon létrejövő egyenesseregek a regulusok; az ellentett irányú egyenesek által alkotott regulust ellentett regulusnak nevezik.

Magasabb dimenzióban[szerkesztés]

Egy i- és egy j dimenziós affin altér a d dimenziós térben kitérő lehet, ha i + j < n. A kitérés definíciója ugyanaz, mint három dimenzióban: azok az alterek kitérők, amelyek se nem párhuzamosak, se nem metszők.

Az affin geometriában bármely dimenziós alterek lehetnek párhuzamosak. Ezzel szemben a projektív geometriában nincsenek párhuzamosok; két altér vagy metsző, vagy kitérő.

Legyen I egy i-, és legyen J egy j dimenziós altér. A d dimenziós projektív térben, ha i + j ≥ d, akkor I és J metszete tartalmaz egy (i+j−d) dimenziós alteret. A magasabb dimenziós véges projektív terek is lefedhetők kitérő alterekkel, hogyha az alterek pontszáma osztója a tér pontszámának. Vagyis, ha a tér rendje q, dimenziója d, és az alterek dimenziója t, akkor $(q^{t}+q^{t-1}+\dots +1)|(q^{d}+q^{d-1}+\dots +1).$

Mindkét geometriában, ha I és J egy k dimenziós altérben metszi egymást egy k ≥ 0-ra, akkor az I ∪ Jponthalmaz meghatároz egy (i+j−k) dimenziós alteret.

Források[szerkesztés]

Joachim Köhler et al.: Analytische Geometrie und Abbildungsgeometrie in vektorieller Darstellung, Diesterweg-Verlag, Frankfurt am Main, 1971, ISBN 3-425-05302-7
Wilmut Kohlmann et al.: Lineare Algebra und Analytische Geometrie, Vieweg-Verlag, Braunschweig, 1977, ISBN 3-594-10826-0
Elisabeth & Friedrich Barth, Gert Krumbacher: Anschauliche Analytische Geometrie, Oldenbourg-Verlag, München, 1997, ISBN 3-486-03500-2
Hilbert, David & Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), Chelsea, pp. 13–17, ISBN 0-8284-1087-9.
Viro, Julia Drobotukhina & Viro, Oleg (1990), "Configurations of skew lines", Leningrad Math. J. 1 (4): 1027–1050, <http://www.math.uu.se/~julia/SplSkrPr.pdf>. Revised version in English: Sablon:Arxiv.
A regulusokról