Hisztogram

A hisztogram metrikusan skálázott tulajdonságok grafikus ábrázolása. Ha túl sok érték szerepel, akkor osztályokba vonják össze őket. Az egyes osztályok szélessége változhat. A mennyiségeket a szorosan egymás mellé rajzolt téglalapok jelölik, ahol az egyes téglalapok területe az adott osztály gyakoriságát mutatja.[1][2][3] A téglalapok magassága az osztály gyakorisági sűrűségét jelöli, ami az adott osztály szélességével leosztott gyakoriság.
A hisztogramok felfoghatók a folytonos valószínűségi változó sűrűségfüggvényének becsléseként.
Matematikai definíciója[szerkesztés]

Általánosabb matematikai értelemben a hisztogram egy függvény, ami az egyes diszjunkt osztályokba tartozó megfigyeléseket számolja. A hisztogram, mint grafikon ennek egy ábrázolási módja. Ha az összes megfigyelések száma, és az osztályok száma, akkor az eleget tesz ennek a feltételnek:
Kumulatív hisztogram[szerkesztés]
A kumulatív hisztogram a megfigyelt mennyiségek kumulatív ábrázolása, ami az eloszlásfüggvényt közelíti. A közönséges hisztogramtól eltérően itt nem az egyes osztályokba eső mennyiségeket, hanem azok összesített számát ábrázolják minden, az adott osztálynál nem nagyobb osztályra. Képlettel, az osztályok kumulatív hisztogramja:
Alkalmazása[szerkesztés]
Hisztogramokat a képfeldolgozásban és a leíró statisztikában használnak. Hisztogramot készítenek, ha:
- a sűrűségfüggvényt, eloszlást szeretnénk becsülni, nemcsak az eloszlás egyes paramétereit
- azt gyanítják, hogy több tényező hat egy folyamatra, és ezt bizonyítani akarják
- értelmes specifikációs határokat akarnak megállapítani egy folyamatra
Elkészítése[szerkesztés]

A hisztogram elkészítéséhez a minta értéktartományát egymást határoló szakaszra, osztályokra bontják.[4] A szélső osztályok ne maradjanak nyíltak, tehát legyen az alsónak alsó, a felsőnek felső határa.[1][5] Az osztályok szélességének nem kell megegyeznie, de segíti az értelmezést, ha legalábbis középen egyenlő szélességűek. Minden osztály fölé akkora területű téglalapot rajzolnak, amekkora arányos az osztály tapasztalati valószínűségével, gyakoriságával.
Gyakorisági sűrűség[szerkesztés]
A téglalapok területe arányos az nj osztálygyakorisággal, ezért a megfelelő hj téglalap magassága , ahol dj az osztály szélessége. A legmagasabb osztály a móduszosztály.[1] Ha az osztályok ugyanolyan szélesek, akkor a gyakorisági sűrűség és a gyakoriság egyenesen arányosak. Ekkor a téglalapok magassága összehasonlítható, és gyakoriságként értelmezhető.
Az osztályok számának meghatározása[szerkesztés]
Az osztályok számára és az osztályok egyenletes szélességére alapvető összefüggés a
Nincs legjobb módszer arra, hogy mikor hány osztály kell. A különböző módszerek mind feltételeznek valamit az eloszlásról. A céltól és az eloszlástól függően különböző osztályszám és szélesség javasolható. A megfelelő osztályszámot és szélességet további kísérletezéssel találják meg. Az osztályok számának meghatározására több ökölszabályt is kitaláltak, pl.:
Mérések száma Osztályok száma <50 5 - 7 50 - 100 6 - 10 100 - 250 7 - 12 >250 10 - 20
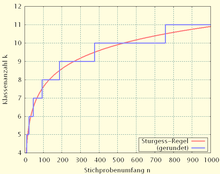
A Sturges-szabály szerint:[6]
A képlet a binomiális eloszlásból származik, és közel normális eloszlást feltételez. Felteszi továbbá, hogy legalább 30 adatpont van. Újabban már nem használják, mert nem veszi figyelembe a szórást.
Az osztályszélesség, Scott szerint:[7]
vagy Freedman és Diaconis alapján:[8]
ahol a szórás, a mérések száma, és a kvartilisek távolsága. Kevésbé érzékeny a távoli pontokra, mint a szórást használó Scott-szabály.
A fenti Scott-szabály csak normális eloszlású adatokra alkalmazható, különben korrekciós tényezőkkel figyelembe kell venni a ferdeséget és a lapultságot is. Normális eloszlásból származó mintán minimalizálja a négyzetes hibát.
A Doane-formula[9] a Sturges-szabály javítása nem normális eloszlású adatokra:
ahol a a lapultságra adott becslés.
Négyzetgyökszabály:
Több diagramszerkesztő, például az Excelé ezt használja.
A rizikófüggvény L2 becslésén alapuló módszer:[10]
ahol a középérték, és a hisztogram torzított szórása a osztályszélességgel. és .
Tulajdonságai[szerkesztés]
A hisztogram a szóban forgó gyakoriságok területarányos ábrázolása. A j-edik téglalap területe megfelel a mennyiségnek, ahol a j-edik osztály relatív vagy abszolút gyakorisága, és arányossági tényező.
Ha ez a arányossági tényező éppen az összes mérés száma, akkor a téglalapok területe megegyezik a megfelelő osztályok abszolút gyakoriságának. Ekkor a hisztogramot abszolútnak nevezik.[11] Ha ez az arányossági tényező 1, akkor a téglalapok területe a relatív osztálygyakoriságokkal egyezik meg. Ekkor a hisztogram relatív vagy normált. Ekkor, mivel a területek a relatív gyakoriságokkal egyeznek meg, az összegük 1.[11]
Az oszlopdiagramtól eltérően az egyes téglalapok az osztályok teljes szélességét kitöltik, ami azt jelenti, hogy a szomszédos téglalapok összeérnek, mivelhogy az egyes osztályok is összeérnek.
Az oszlopdiagramtól eltérően a hisztogram x tengelyén is mennyiségeket kell felvenni. Az értékeknek rendezetteknek és skálázhatóknak kell lenniük.
A hisztogramról a következők olvashatók le elsősorban:
- a görbe lefutása
- a centráltság
- a szórás
Példa[szerkesztés]
32 európai országban mérték az ezer főre jutó autók számát. Az értékeket a következőképpen osztályozták:

| A j osztály | Az 1000 főre jutó autók száma | Az országok száma (abszolút osztálygyakoriság) nj |
Osztályszélesség dj |
Magasság (gyakorisági sűrűség) hj = nj/dj |
| 1 | 0 - 200 | 5 | 200 - 0 = 200 | 0,025 |
| 2 | 200 - 300 | 6 | 100 | 0,06 |
| 3 | 300 - 400 | 6 | 100 | 0,06 |
| 4 | 400 - 500 | 9 | 100 | 0,09 |
| 5 | 500 - 700 | 6 | 200 | 0,03 |
| Összeg Σ | 32 |
A vízszintes tengelyre az osztályok közepét és határait vitték fel. A függőleges tengelyen nem készítenek beosztást, nehogy a magasságot nézzék gyakoriságnak a terület helyett. Ez a veszély azonban nem áll fenn, ha az osztályok egyformán szélesek, mivel ekkor a magasság is arányos a gyakorisággal; ekkor az nj-k ábrázolhatók a függőleges tengelyen.
A Statistics Online Computational Resource (SOCR) oldalai sok interaktív bemutatót tartalmaznak a hisztogramok készítéséről[12] és kezeléséről.[13]
Átlageltolt hisztogramok[szerkesztés]
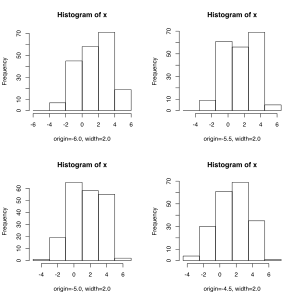
A bal kép négy hisztogramot mutat ugyanarról az adathalmazról. Mindegyiken 0,2 az osztályszélesség, alakjuk mégis eltér, mivel máshol kezdődik az első osztály: -6,0; -5,5; -5,0 és -4,5. Ez a példa jól mutatja, hogy az osztályszélesség és az osztályok száma mellett a bal osztályhatár is fontos. David Scott ezért átlageltolt (average-shifted) hisztogramot javasolt.[14]
A jobb képen átlageltolt hisztogramot láthatunk. A négy hisztogramot egymásra helyezve és minden x értékre kiátlagolva kapták a függőleges tengelyre felmért magasságokat. A gyakorlatban lényegesen több előzőleg elkészített hisztogramot átlagolnak ki így. Az átlageltolt hisztogramot a hisztogram és a magsűrűségbecslés közé helyezik el. Az átlageltolás megoldja a bal osztályhatár problémáját, de nem segít az osztályok számának meghatározásában.
-
Négy hisztogram ugyanarról az adatsorról. Az osztályszélesség mindegyiken 2,0. Az első osztály kezdete azonban rendre -6,0; -5,5; -5,0 és -4,5
-
Átlageltolt hisztogram a bal oldalon látható négy hisztogram kiátlagolásából
A képfeldolgozásban[szerkesztés]

A digitális képfeldolgozásban a hisztogram a kép színértékeiről vagy szürkeségi fokozatáról készül. Ez alapján adatok nyerhetők az előforduló színekről, kontrasztokról és fényességekről. Egy színes képről több hisztogram is készíthető az egyes színcsatornák, vagy az összes szín szerint. Mivel a legtöbb eljárás a fekete-fehér képeket támogatja, ezért inkább az egyes színcsatornák hisztogramját használják, ami lehetővé teszi a kép feldolgozásának azonnali folytatását. A színcsatornák száma az alapszínek számától függ: RGB estén három, CMYK esetén négy.
A kép hisztogramja a fényességértékek eloszlását mutatja. A lehetséges színértékek tengelyére az egyes színértékek gyakoriságát viszik fel. Minél magasabb ez, annál többször fordul elő az adott színérték a képen.
A digitális fényképészet gyakran használ hisztogramot. A jól felszerelt digitális fényképezőgépek valós időben mutatnak hisztogramokat, hogy így segítsék a képi egyensúly megtalálását. Ez pontosabb képszerkesztést tesz lehetővé, mint ami a kamerakép alapján lehetséges lenne. Felismerhetők és javíthatók például a világítás hibái, ha a kép túl sötét vagy túl világos lenne. A kép későbbi feldolgozásában sokat számítanak a rajta levő kontrasztok és a fényességek, ezért érdemes a hisztogramokat figyelni.
A hisztogramok egy klasszikus felhasználása a színegyensúly beállítása (equalizing). A hisztogramot és a megfelelő színeket egy alkalmas függvénnyel transzformálják. Jobban kiegyensúlyozza a színeket, mint a kontrasztok erősítése.
Alacsony és magas kulcsú fényképészet[szerkesztés]

Az alacsony kulcsú fényképészetben a kép részletei, pixeljei az alacsony tónusértékeken koncentrálódnak; a kép sötét. A hisztogramon a legtöbb pixel az alacsony tartományban szerepel.
A magas kulcsú fényképészetben ellenben a pixelek a magas értékeken koncentrálódnak. A kép világos.
Ha a kép túl van világosítva, akkor az értékek eltolódnak a magasabb értékek felé. A hisztogram szerint a maximum nem éretik el. Ez azt mutatja, hogy sok kis részlet kimarad a képről, mivel le lett vágva egy fényességi tartomány, és ami olyan fényes, az a képen fehér.
Története[szerkesztés]
A hisztogramok először William Playfair skót mérnök és közgazdász 1786-ban megjelent Kereskedelmi és politikai atlasz (The Commercial and Political Atlas) című művében bukkantak fel.[15] Ő vezette be korábban a vonal- és a kördiagramot is. 1833-ban a francia André-Michel Guerry hisztogramokkal jelenítette meg az adatokat.[16] Adolphe Quetelet belga statisztikus és szociológus 1846 körül továbbfejlesztette a hisztogramot. Magát a „hisztogram” (historical diagram)[17] szót először Karl Pearson angol matematikus használta 1891-ben az előadásain, és 1895-ben a mai jelentésében vezették be.[18][19][20]
Jegyzetek[szerkesztés]
- ↑ a b c szerk.: Gabler Verlag: Lexikon Statistik, 157. o. (1994)
- ↑ szerk.: Springer: All of Nonparametric Statistics, 127. o. (2005)
- ↑ szerk.: Spektrum Akademischer Verlag: Mathematik. 2008, 1226. o.
- ↑ Thomas A. Runkler: Data Mining: Methoden und Algorithmen intelligenter Datenanalyse. (angolul) 1. (hely nélkül): Vieweg + Teubner. 2010. 47. o.
- ↑ Erhard Cramer – Udo Kamps: Grundlagen der Wahrscheinlichkeitsrechnung und Statistik: Ein Skript für Studierende der Informatik, der Ingenieur- und Wirtschaftswissenschaften. (németül) 2. (hely nélkül): Springer. 2008. 45. o.
- ↑ Herbert A. Sturges: The choice of a class interval. (angolul) 1926. 65–66. o. = Journal of the American Statistical Association, 21.
- ↑ David W. Scott: On optimal and data-based histogram. 3 (angolul) 1979. 605–610. o. = Biometrika, 66. doi:10.1093/biomet/66.3.605
- ↑ David Freedman, Persi Diaconis: N the histogram as a density estimator: theory. 57 1981. 453–476. o. = Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, 4. doi:10.1007/BF01025868
- ↑ Doane DP (1976) Aesthetic frequency classification. American Statistician, 30: 181–183
- ↑ Shimazaki, H., Shinomoto, S. (2007). „A method for selecting the bin size of a time histogram”. Neural Computation 19 (6), 1503–1527. o. DOI:10.1162/neco.2007.19.6.1503. PMID 17444758.
- ↑ a b Jürgen Bortz: Statistik für Human- und Sozialwissenschaftler. (németül) 6. (hely nélkül): Springer. 2005. 31–32. o.
- ↑ Mixture Model 1
- ↑ Power Transform Family Graphs
- ↑ David Scott: Multivariate Density Estimation: Theory, Practice, and Visualization. (angolul) (hely nélkül): John Wiley. 1992. ISBN 978-0471547709
- ↑ Playfair, William; The Commercial and Political Atlas: Representing, by Means of Stained Copper-Plate Charts, the Progress of the Commerce, Revenues, Expenditure and Debts of England during the Whole of the Eighteenth Century, London 1786
- ↑ André-Michel Guerry: Essai sur la Statistique Morale de la France. (franciául) Paris: (kiadó nélkül). 1833.
- ↑ „He explained that the histogram could be used for historical purposes to create blocks of time of ‘charts about reigns or sovereigns or periods of different prime ministers’.“. The Rutherford Journal
- ↑ Sheldon M. Ross: Introductory Statistics. (angolul) 2. (hely nélkül): Elsevier Academic Press. 2005. 56–57. o.
- ↑ Yadolah Dodge: The Concise Encyclopedia of Statistics. (hely nélkül): Springer. 2008. 236–237. o.
- ↑ Eileen Magnello: Karl Pearson's Gresham Lectures: W. F. R. Weldon, Speciation and the Origins of Pearsonian Statistics. (angolul) (hely nélkül): Cambridge University Press. 1996. 48. o. = The British Journal for the History of Science, Vol. 29, No. 1,












![{\displaystyle h={\frac {3{,}49\cdot \sigma }{\sqrt[{3}]{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/948dbdf3ed0076828691aafb3742663f22c06336)
![{\displaystyle h={\frac {2\cdot (Q_{3}-Q_{1})}{\sqrt[{3}]{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0d0239894c9729467766b88f4a29f02f5b5e812)