Bolygómű
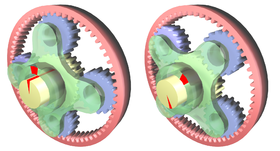

A bolygóművek (angolul: Epicyclic gearing vagy planetary gearing) olyan fogaskerekes vagy dörzskerekes mechanizmusok, melyek két kerékrendszerből állnak. Az egyik kerékrendszer tengelye rögzített, mely körül a kerekek foroghatnak. Ugyanezen tengely körül foroghat az úgynevezett híd is, mely csillag alakú alkatrész. A másik kerékrendszer tengelyei a hídba vannak szerelve úgy, hogy fogaik kapcsolódnak az első kerékrendszer kerekeihez. Ezek a kerekek egyrészt a saját tengelyük, másrészt a rögzített tengely körül is forognak. Az egész mechanizmus a Nap körül keringő bolygók mozgásához hasonló működést mutat (azzal a különbséggel, hogy a pályák mindig köralakúak), ezért az első csoport kerekeit napkeréknek, a másodikéit pedig bolygókeréknek hívják.
A bolygóművek működése[szerkesztés]
A bolygóhajtóműveknél az egyik kerékrendszer rögzített, egy másik a behajtó, míg a harmadik a kihajtó elem. Attól függően, hogy a három kerékrendszerből melyiket rögzítik, ugyanaz a bolygóhajtómű más-más áttételt valósít meg. Az első két ábrán látható bolygóművek egyszerű hajtások, gyakran több bolygóhajtást kapcsolnak össze, melyekkel változatos feladatokat lehet megoldani. Az egyik lehetőség az, hogy a hajtásláncba elágazások építhetők be, vagyis több kihajtótengely is megvalósítható (ezeket osztóműnek hívják), vagy több behajtás is dolgozhat egy kihajtásra, ezek az összehajtások. Természetesen megvalósítható olyan szerkezet is, melyben összehajtás és osztás is működik. A hibrid hajtású gépkocsik erőátvitele tipikus példa erre az utóbbira: a járművet egyrészt hagyományos Otto-motor vagy dízelmotor hajtja, másrészt elektromos hajtás is besegít, adott üzemviszonyok esetén, ehhez általában bolygóhajtóművet használnak, mely önműködően összegezi a két erőforrás teljesítményét. Másrészt a sebességváltóról egyrészt a gépkocsi kerekeinek hajtása ágazik el, másrészt az akkumulátorok feltöltésére szolgáló generátor hajtása. Végül a differenciálmű – mely szintén bolygóhajtás – osztja el a nyomatékot a meghajtott kerekekre.
Áttétel[szerkesztés]
Az alábbi táblázat néhány gyakrabban használt rendszer kimenő fordulatszámát adja meg a behajtó tengely(ek) fordulatszámának függvényében, melyből az áttétel az alábbiak szerint számítható:
ahol
- a behajtó és kihajtó tengely fordulatszáma,
- a behajtó és kihajtó tengelyen ébredő forgatónyomaték.
| Elnevezése | Fogszáma | Fordulatszáma |
|---|---|---|
| Vázlat | Áttétel | Vázlat | Áttétel | Vázlat | Áttétel | Vázlat | Áttétel |
|---|---|---|---|---|---|---|---|

|

|

|

|
||||

|

|

|

|
||||

|

|

|

|
||||

|

|

|

|
||||

|

|

|

|
||||

|
|

|

|
Alkalmazások[szerkesztés]

Bolygóhajtóműveket elsősorban nagy áttételek esetén alkalmaznak, ahol a kis méretek is fontosak. Ilyenek például az emelőgép- és daruhajtóművek, radarberendezések hajtása. Nehéz munkagépek és terepjárók kerekeinél használható mint véglehajtás, így az egész erőátviteli láncot – a nagyobb fordulatszám miatt – kisebb nyomatékkal kell terhelni. Indítómotoroknál is elterjedt mint nyomatéknövelő megoldás.
Az a lehetőség, hogy egy adott bolygókerékhajtás attól függően, hogy melyik elemét rögzítik, más és más áttételt valósít meg, váltóművekben, sebességváltókban jelent nagy előnyt. A Galamb József tervezte híres Ford T-modell gépkocsi sebességváltója egymás után kapcsolt bolygókerekes fokozatokból állt, a sebességváltás az egyes fokozatok szalagfékkel való lefékezése (rögzítése) által valósultak meg. A bolygókerekes hajtóműveknél lehetőség nyílik a primer behajtás mellett egy másodlagos behajtás megvalósítására is (lásd a táblázat utolsó sorát). Ez lehetővé teszi olyan sebességváltó készítését, ahol a másodlagos behajtást egy fokozatmentes hajtás végzi, ezzel a teljes hajtás fokozatmentes hajtássá alakítható azzal együtt, hogy csökkenthetők a fokozatmentes hajtások nagyobb veszteségei. A leggyakrabban használt bolygókerekes hajtások a gépkocsik differenciálművei.
A primer és szekunder hajtás lehetőségét használja ki a Toyota Prius hibrid hajtású gépkocsi bolygókerekes sebességváltója is, ahol a napkereket az elektromotor hajtja, a belső fogazatú koszorút pedig a dugattyús motor.
Előnyök-hátrányok[szerkesztés]
A bolygóhajtóművek előnyei: nagy teljesítménysűrűség (kis térfogatban nagy teljesítményt visz át), nagy áttétel megvalósítása kis méretekben, több kinematikai lehetőség választása, csak csavaró reakciók ébredése, a bemenő és kimenő tengely egy egyenesbe esik. Hátrányai: nagy csapágyterhelések, nehezen szerelhető és hozzáférhető, bonyolult tervezés.
További információk[szerkesztés]
- Daruhajtómű hallgatói terv 1.[halott link]
- Daruhajtómű hallgatói terv 2.[halott link]
- Daruhajtómű hallgatói terv 3.[halott link]
- Dr. Szabó András: Hajtástechnika
- Bolygóhajtás animáció
- Toyota Prius sebességváltó működése (angolul)
- Interaktív bolygómű animáció
Források[szerkesztés]
- Pattantyús Gépész- és Villamosmérnökök Kézikönyve 3. kötet. Műszaki Könyvkiadó, Budapest, 1961.


































![{\displaystyle {\color {red}n}={\color {blue}n}\left[1-\left({\frac {\color {magenta}n}{\color {blue}n}}-1\right){\frac {\color {magenta}z}{\color {red}z}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9239bbfe93b3c73d416cf065b5349fa212e6faf3)

