Függvény (matematika)

A függvény vagy más néven parciális (részleges) leképezés a matematika egy olyan absztrakt fogalma, mely a geometriai leképezések, elemi algebrai műveletek, folytonosan változó mennyiségek és hasonló, bemeneti értékekből egyetlen kimeneti értéket produkáló fogalmak általános leírására szolgál. Az függvény a halmaz – melyet az értelmezési tartományának nevezünk – minden egyes eleméhez egyetlen kimeneti értéket rendel. Hagyományosan ezt így jelölik:
- , ahol vagy
- , ahol
A függvény fogalmához szorosan hozzátartozik az az elv, hogy két függvényt akkor tekintünk egyenlőknek, ha értelmezési tartományuk ugyanaz és a közös értelmezési tartomány minden egyes eleméhez a két függvény ugyanazt az értéket rendeli.
Szabatos matematikai fogalmazásban, függvényen általában úgynevezett jobbról egyértelmű hozzárendelést értünk. A függvény fogalma tehát a reláció (más néven: hozzárendelés) fogalmának olyan speciális esete, melyben bármely adott dologhoz legfeljebb egy dolgot rendelünk hozzá.
Ha ezen felül megköveteljük azt is, hogy a függvény minden ilyen dologhoz legalább egy dolgot hozzárendeljen, azaz ha a reláció bármely adott dologhoz pontosan egy dolgot rendel hozzá, akkor függvény helyett totális függvényről (illetve parciális leképezés helyett leképezésről) beszélünk.
Formális definíció[szerkesztés]
A mindennapi matematikai gyakorlatban alkalmazott informális függvényfogalmat (a bevezetőben lényegében erről beszéltünk) többféleképpen lehet szabatos formulákban megfogalmazni. Attól függően, hogy az alkalmazás inkább algebrai, analitikus, geometriai vagy matematikai logikai, a következő formális definíciókkal, egymástól néha fogalmilag is különböző értelmezésekkel találkozhatunk.
Első definíció[szerkesztés]
- Ezt az alakot elsősorban a halmazelméletben és az analízisben használják.
A halmazelméletben függvényen rendezett párok olyan halmazát értjük, amiben első komponensként legfeljebb csak egyszer szerepelhet egy elem - az utóbbi, ún. egyértelműségi tulajdonság logikai formulában kifejezve:
Értelmezési tartomány, értékkészlet[szerkesztés]
Ebben az esetben az függvény értelmezési tartománya:
halmaz, mely biztosan halmaznak tekinthető a részhalmaz-axióma miatt, hiszen része az rendezett párjai második komponenseinek halmazának.
Az értékkészlete:
- ;
mely a részhalmaz-axióma miatt tényleg halmaz. Gyakran találkozunk a következő szimbólumokkal:
- , , , , ,
ahol a ran rövidítés a „range of function ” angol kifejezés rövidítése (hasonlóképpen az Im az „image of function ” az értékeinek halmazára utal).
Az értelmezési tartomány minden egyes eleméhez egyetlen olyan elem tartozik, melyre , mely egyértelműen létező -t ebben az esetben is
jelöli.
Második definíció[szerkesztés]
Legáltalánosabb esetben függvényen olyan rendezett hármast értünk, ahol és két halmaz, pedig olyan reláció, hogy minden elemre legfeljebb egyetlen olyan létezik, melyre teljesül.
Ekkor az -t alaphalmaznak vagy kiindulási halmaznak, a -t képhalmaznak vagy érkezési halmaznak nevezik. értelmezési tartományán a értelmezési tartományát értik, azaz az azon részhalmazát, melynek minden eleme esetén pontosan egy olyan található, hogy , azaz melyre -t leszűkítve az balról totális reláció lesz. értékkészletén a értékkészletét értik, azaz azon elemek halmazát, melyre létezik , hogy .
Ha az így megadott függvény esetén az értelmezési tartománya nem esik egybe az alaphalmazával, akkor azt mondjuk, hogy parciális vagy parciálisan értelmezett függvény. Ellenkező esetben totális függvényről beszélünk.
Harmadik definíció[szerkesztés]
- Ez a definíció általában az algebrára, a geometriára és a konkrét kategóriák elméletére jellemző. Ekkor a függvény egy speciális relációs struktúra.
Az f függvény olyan (A, B, ρ) rendezett hármas, ahol A és B egy-egy halmaz, ρ pedig olyan A × B-beli reláció, melyre teljesül, hogy minden egyes A-beli x-hez pontosan egy olyan B-beli y van, melyre x ρ y. Ekkor tetszőleges x ∈ A elemhez az f által egyértelműen rendelt elemet f(x)-szel jelöljük.
Értelmezési tartomány[szerkesztés]
Ha (A, B, f) egy, a fenti értelemben vett függvény, akkor az A halmazt az értelmezési tartományának, definíciós tartományának nevezzük. Jelölése nem egységes, a leggyakrabban a következők fordulnak elő:
- , , , , .
A Dom(f) jelölés az angol „definition domain of function f” (az f értelmezési tartománya) kifejezés rövidítéséből származik.
Érkezési halmaz[szerkesztés]
Az (A,B, f) függvény esetén a B halmaz az f függvény érkezési halmaza, melyet a fenti definíció esetén az f függvény egyértelműen meghatároz. Ha jelölik valahogy, leggyakrabban a
jelölést használják, az angol „codomain of function f” kifejezés rövidítéseként (ez hasonló a kovektor és koszorzat latin eredetű kifejezésekhez, egyfajta megfordított irányt jelöl).
Értékkészlet[szerkesztés]
Egy , a második konvencióban definiált függvény érkezési halmaza nem tévesztendő össze az értékkészlettel, mely az
halmaz.
Azt, hogy egy olyan függvény, melynek értelmezési tartománya , az értékkészlete pedig része a halmaznak, a következőképpen jelöljük:
Egy függvény tehát az halmaz minden egyes eleméhez hozzárendel egy -beli értéket.
A logikai grammatika függvényfogalma[szerkesztés]
A fenti definíciók szemlélete a halmazelméleti realizmus talaján áll. Ám, a függvényfogalom bevezethető a Frege és Hilbert által javasolt módon is, mely az informális matematika nyelvi elemzését veszi alapul. Eszerint egy függvény nem más, mint egy egyváltozós névfunktor, tehát mely egy individuumnévből nevet alkot. (A matematikai logikában ezen kívül a függvénynek nevezik a több-bemenetű névfunktorokat is, azaz a műveleteket.) Egy ilyen névfunktor például a csoportelmélet formális nyelvében az elem inverzének képzése (a−1) és az aritmetikában a természetes számok rákövetkezési operátora ( s(a) ).
Példák[szerkesztés]
Példaként említünk az algebra, a geometria és az analízis egy-egy függvényét:
- Legyen abs: z |z|, ahol z ∈ C. Ez a függvény a z komplex számhoz abszolút értékét, vagy hosszát adja, mely egy nemnegatív valós szám: .
- Legyen Tt a sík egy adott t tengelyére történő tükrözése. Ekkor a T:P P' függvény egy geometriai leképezés, a sík egy tetszőleges P pontja esetén P' =T(P) a P pont t-re vonatkozó tükörképe.
- exp: x ex, a természetes alapszámú exponenciális függvény, ahol tehát az alap az e Euler-féle szám.
- Példák függvénygrafikonokra
-
Lineáris függvény
-
Ötödfokú polinom
-
A komplex exponenciális függvény valós része
-
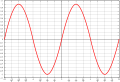
Szinuszfüggvény
-
A normális eloszlás sűrűségfüggvénye
A függvények osztályzása[szerkesztés]
Injektív, szürjektív, bijektív[szerkesztés]
Az értelmezési tartomány egy elemének képe az értékkészletnek az az eleme, amit a függvény hozzárendel.
Egy érték ősképe az értelmezési tartománynak az a részhalmaza, melynek elemeihez azt az értéket rendeli a függvény. Ez általában nem egyelemű, hiszen például az
- függvény a 2, -2 számokhoz is a 4-et rendeli értékként.
Ha az értékkészlet minden elemének ősképe egyelemű, akkor a függvény injektív. Az injektív tulajdonság ereje abban áll, hogy ezek a függvények invertálhatók, azaz inverz relációjuk is (parciális) függvény.
Egy függvény szürjektív, ha az érkezési halmaz minden eleme előáll képként, tehát nem tekintettünk az értékkészletnél bővebb halmazt érkezési halmaznak. Például, ha az
- függvény érkezési halmazának -t tekintjük, akkor nem szürjektív, hiszen a negatív egészek nem állnak elő.
Ha egy függvény injektív és szürjektív, akkor bijektív. Ez azt jelenti, hogy az érkezési halmaz minden elemének ősképe pontosan egyelemű. Ezt használják a halmazok számosságának megadására is.
A változók száma szerint[szerkesztés]

A változók száma szerint beszélünk egyváltozós, kétváltozós, illetve többváltozós függvényről. Formálisan, egy függvény kétváltozós, ha . Nem elfajuló esetben lehet részhalmaz is az értelmezési tartomány. Ekkor az függvény az párhoz az értéket rendeli. Hasonlóan, egy függvény háromváltozós. Egy függvény akkor egyváltozós, ha az értelmezési tartomány nem áll elő szorzathalmazként, illetve az értelmezési tartomány belső szerkezetétől eltekintünk. Ha a függvény értékkészlete egyetlen elem, akkor a függvény nulla változós, konstans.
Itt megjegyezzük, hogy ez a fogalom a matematika elterjedt, sztenderdnek tekinthető halmazelméleti felépítésében pusztán technikai, ill. formai jellegű. A valós számok halmazán értelmezett valamely kétváltozós függvényt - pl. f(x,y)=x+y - lényegében egyváltozósnak is tekinthetjük, amely értelmezési tartománya a valós számok halmazának Descartes-szorzata önmagával, az értékkészlete pedig a valós számok halmaza. A geometriai transzformációk a sík, illetve a tér pontjait transzformálják, mégis többnyire egyváltozós, pont-pont függvényeknek tekintjük őket.
Egy másik felfogás szerint a többváltozós függvények lebonthatók egyváltozós függvényekre. Például az függvény tekinthető úgy, mint ami a független a változóhoz hozzárendeli annak b-vel növelt értékét. Ezt körrizésnek nevezik, és inkább az informatikában jut szerephez.[1]
Az alaphalmaz szerint[szerkesztés]
- Valós függvény
- Komplex függvény
- Geometriai leképezés
- Vektorterek leképezése
stb.
Analitikai tulajdonságok[szerkesztés]
- Korlátosság
- Periodikusság
- Monotónia
- Paritás
- Folytonos függvény
- Differenciálhatóság
- Holomorfia
- Homogenitás
- Mérhetőség
- Integrálhatóság
- Konvex vagy konkáv
A műveletekkel való kifejezhetősége szerint[szerkesztés]
- Sorozat: a pozitív egészeken (1-től indexelve) vagy a természetes számokon (0-tól indexelve) értelmezett függvény
- Számelméleti függvény: az egész számokon értelmezett függvény
- Valós értékű függvény: a valós számokba képező függvény
- Komplex értékű függvény: a komplex számokba menő függvény
- Egészrész és törtrészfüggvény
- Maximum és minimum
- Algebrai függvény
- Homogén lineáris függvény: alakú függvény, homomorfizmus az összeadásra
- Lineáris függvény, avagy affin függvény: alakú függvény
- Kvadratikus, vagy másodfokú függvény: alakú függvény, ahol .
- Racionális egészfüggvény, polinom: vagy alakú függvények
- Racionális törtfüggvény
- Racionális függvény, lásd racionális egészfüggvény és racionális törtfüggvény
- Gyökfüggvény: egy gyökvonást és alapműveleteket tartalmazó függvény
- Transzcendens függvény
- Exponenciális függvény
- Logaritmusfüggvény
- Trigonometrikus függvények
- Abszolútérték-függvény
- Hiperbolikus függvények
vagy például
- Izometrikus leképezés
- Affin transzformáció
- Inverzió
- Hasonlósági leképezés
- Elsőfokú racionális egészfüggvény
- Másodfokú racionális egészfüggvény
- Harmadfokú racionális egészfüggvény
(itt megjegyzendő, hogy ez az osztályozás nem teljes és rendszerezésre vár)
Függvények halmaza[szerkesztés]
A jelölések a -ből -be menő leképezéseket jelölik:
A halmaz számosságára teljesül, hogy:
Függvények megadása[szerkesztés]
Egy f függvényt akkor tekintünk adottnak, ha adott
- értelmezési tartománya és
- az értelmezési tartomány minden x eleme esetén az ehhez rendelt f(x) érték – ezt a hozzárendelési utasításnak nevezzük.
Ezek már meghatározzák az értékkészletet, ám nem határozzák meg a függvény érkezési halmazát. Ha a függvény fogalmát a fenti, algebrai szemléletben definiáljuk, akkor ezeken kívül még meg kell adnunk az érkezési halmazát is.
A hozzárendelést egy
vagy
alakban adott szimbólumsorral jelöljük. (Az utóbbi jelölésben a hozzárendelést leggyakrabban „talpasnyíllal” jelölik.) A H halmaz az értelmezési tartomány, vagyis amilyen értékeket a formula x változója helyére helyettesíthetünk, a K az érkezési halmaz, azaz amilyen értékeket a függvényérték, azaz f(x) felvehet.
Például:
Néha megengedjük az értelmezési tartomány helyett egy azt tartalmazó bővebb halmaz megadását, azzal a kimondatlan kiegészítéssel, hogy az értelmezési tartomány az a részhalmaz, amire a hozzárendelési utasításban szereplő kifejezések értelmezve vannak. Ez akkor célszerű, ha már az is komoly vizsgálatot igényelne, hogy megmondjuk, milyen elemekre végezhetők el a hozzárendelési utasításban szereplő műveletek. Néha, ekkor a nyíl „kiindulási halmaz” felőli végére egy részhalmaz jelet teszünk. Például:
A hozzárendelési utasítás megadásának eddigi, tehát y = f(x) formáját explicitnek nevezzük és azt mondjuk, hogy a függvényt explicit módon adott. Az y = f(x) formális egyenlőséget egy y-ra nem rendezett (implicit) egyenlettel sokszor egyszerűbb megadni. Ekkor azt mondjuk, hogy a függvény implicit módon adott. Az implicit megadásnál azonban ügyelnünk kell arra, hogy ekkor a függvény nem feltétlenül egyértelmű.
- Lásd még: implicitfüggvény-tétel.
Függvények relációalgebrája[szerkesztés]
- Fő szócikk: Függvények relációalgebrája
A relációkalkulusból átöröklött tulajdonságok definiálhatóak és vizsgálhatóak függvények esetében is. A legfontosabbak a balról totalitás (szürjektivitás), a jobbról egyértelműség (injektivitás) és a kölcsönösen egyértelműség vagy bijektivitás.
Hasonlóan, a bináris relációkra értelmezett halmazelméleti (unió, metszet, különbség, megszorítás) és algebrai (szorzás v. kompozíció; invertálás stb.) műveletek is értelmezhetőek - lényegi változtatás nélkül - és vizsgálhatóak függvényekre is.
Egy függvény konstans, ha az értelmezési tartomány minden eleméhez ugyanazt az értéket rendeli. Ekvivalensen, értékkészlete egyelemű.
Egy függvény idempotens, ha egyenlő önmaga kompozíciójával. Azaz, ha idempotens, akkor , azaz a teljes értelmezési tartományon.
Az identitás az a függvény, ami az értelmezési tartomány minden eleméhez önmagát rendeli. Azaz a teljes értelmezési tartományon.
Egy függvény involúció, hogyha , vagyis a teljes értelmezési tartományon, továbbá van legalább egy eleme az értelmezési tartománynak, hogy (ami kizárja az identitást). Algebrai nyelven szólva, másodrendű függvény, avagy rendje kettő.
Ha az függvény értelmezési tartományának eleme, és , akkor az függvény fixpontja.
Műveletek[szerkesztés]
Ha adott egy H halmaz, melyen értelmezett egy * művelet, akkor egy A halmazból a H-ba képező függvények körében értelmezhető a pontonkénti művelet a következőképpen:
melynek ugyanolyan algebrai tulajdonságai vannak, mint a * műveletnek. Például az R R függvények körében értelmezhető az f + g összeg, az f g szorzás, és a fenti definíció csekély módosításával a λf számmal való szorzás és az f/g osztás (g nemnulla értékű helyeire).
Ha függvény, akkor korlátozása, leszűkítése, megszorítása az halmazra az függvény, melynek grafikonjára teljesül, hogy
Ha bijektív, akkor inverz relációja egy függvény, melyre minden esetén teljesül, hogy ha , akkor minden esetén. Tehát
- .
A bijektív függvényeket invertálható függvénynek is nevezik. Ha egy függvény injektív, de nem szürjektív, akkor, mivel nincs minden képnek ősképe, azért az inverz reláció nem rendel minden képhez ősképet. Ha egy függvény szürjektív, de nem injektív, akkor inverz relációja valamely képhez több ősképet is rendel.
Ha és függvények, akkor komponálhatók. A művelet feltétele, hogy az első függvény értékkészletét a második függvény értelmezési tartománya tartalmazza. A kompozíció eredménye az a függvény, melyre
A műveletben a jelölésben g a külső, f a belső függvény. Általában ebben a sorrendben találjuk meg a kompozíció operandusait a szakirodalomban.
Valós értékű függvények nevezetes pontjai[szerkesztés]
A H halmazon értelmezett, R-be képező f függvénynek az a ∈ H pontban
- abszolút minimuma van, ha minden x ∈ H-ra f(a) ≤ f(x); ekkor a minimumérték az f(a);
- lokális minimuma van, ha H topologikus tér és létezik a-nak olyan V ⊆ H nyílt környezete, hogy az f|V leszűkítésnek abszolút minimumhelye a;
- abszolút maximuma van, ha minden x ∈ H-ra f(x) ≤ f(a) ; ekkor a maximumérték az f(a);
- lokális maximuma van, ha H topologikus tér és létezik a-nak olyan V ⊆ H nyílt környezete, hogy az f|V leszűkítésnek abszolút maximumhelye a.
- zérushelye van, ha f(a) = 0;
- stacionárius pontja van, ha H normált tér, f differenciálható az a egy nyílt környezetén és a differenciálja ott nulla: df(a)=0.
A minimum- vagy maximumértéket együttesen szélsőértéknek, azok abszcisszáját szélsőértékhelynek nevezzük.
Függvényterek mint struktúrák[szerkesztés]
A függvények abból a szempontból is alapvető matematikai fogalmak, hogy számos elmélet konkrét megvalósítását függvények halmazaiban láthatjuk. Például
- a sorozatok tekinthetők a természetes számok halmazán értelmezett függvényeknek
- az n×k-as mátrixok tekinthetők az {1,…,n}×{1,…,k} Descartes-szorzaton értelmezett függvények halmazának
- a logikai relációk megfeleltethetők az {igaz, hamis} halmazba képező függvényeknek
- egy vektortér duális tere nem más, mint a vektortérből az alaptestbe ható lineáris függvények halmaza
- homeomorfiák topologikus terek szerkezetének vizsgálatához
- homomorfiák, izomorfiák csoportjai különböző struktúrákon
és még számos példa hozható fel, amikor absztrakt matematikai tereket függvények halmazaival azonosítanak, praktikusan minden matematikai részterületen.
Általánosítás[szerkesztés]
Multifüggvények[szerkesztés]
A multifüggvények balról totális relációk, azaz az alaphalmaz minden eleméhez hozzárendelnek legalább egyetlen elemet. Jelölje az értelmezési tartományt, az értékkészletet! Ekkor, ha f multifüggvény, akkor .
Ha halmaz, akkor minden multifüggvény tekinthető függvénynek az hatványhalmazába: .
A multifüggvények kompozíciója ugyanúgy definiálható, mint a függvényeké. Halmazelméleti szempontból ez két reláció kompozíciója.[2]
A multifüggvények lehetnek szürjektív függvények inverz relációi. Ha szürjektív, akkor automatikusan multifüggvény. Egy szürjektív függvény és inverz multifüggvényének kompozíciója ekvivalenciareláció, a függvény által indukált ekvivalenciareláció. Ebben a relációban két elem ekvivalens, ha a függvény ugyanazt az értéket rendeli hozzá.[2]
Parciális függvények[szerkesztés]
Egy reláció parciális függvény, ha az alaphalmaz minden eleméhez legfeljebb egy elemet rendel. Előfordul, hogy a függvényeket parciális függvényként definiálják, ekkor az általában függvénynek tekintett relációkat totális vagy teljes függvénynek nevezik.
A -ből -be menő parciális függvények halmaza megegyezik a részhalmazait -be képező totális függvények halmazával:
Véges halmazok esetén kardinális számaikra:
- .
Minden parciális függvény kiterjeszthető totálissá úgy, hogy az értékkészlethez egyenként hozzáveszünk egy újabb elemet, amit hozzárendelünk egy olyan elemhez, aminek nincs képe az eredeti képhalmazban. Ezekkel a bővítésekkel végül bijektív függvényhez jutunk.
Minden parciális függvény lényegében egyenlő a totális függvénnyel, ahol az ősképhalmaz .
Osztályból vagy osztályba képező függvények[szerkesztés]
A felsőbb matematikában gyakori, hogy egy függvény értékei egy valódi osztály elemei. Erre példák a halmazsorozatok, ahol az értelmezési tartomány , az értékkészlet pedig egy matematikai elmélet objektumai közül kerülnek ki, amik valódi osztályt alkothatnak. Az ebből adódó halmazelméleti problémák megkerülhetők, amennyiben a grafikon egy halmaz. Pontosabban, egy függvényszerű grafikon rendezett párok halmaza úgy, hogy az első elemek nem ismétlődnek. Ha e párok halmazát jelöli, akkor:[3]
Az értelmezési tartomány és az értékkészlet valójában halmazok, de nincs szükség arra, hogy előre meghatározzuk az értékkészletet, amennyiben a függvények lényegileg egyenlők. Parciiális függvények esetén hasonló a helyzet: nincsenek halmazelméleti problémák, mindaddig, amíg a grafikon halmaz marad.
Szimbólumok[szerkesztés]
A függvényekhez létezik néhány szimbólum, melyekkel a függvények speciális tulajdonságait fejezik ki. A következő táblázat tartalmazza a legfontosabbakat.
| Szimbólum | Leírás |
|---|---|
| Függvény -ból -be | |
|
Függvény, ami -t -re képezi; helyett term is állhat |
|
Függvény, ami -t -re képezi; helyett állhat képlet is |
| Függvény, ami -t -re képezi, elemenkénti hozzárendelést jelöl függvényszimbolikával (ahelyett, hogy állhatnak és hasonlók) és helyett egy képlet, amivel a kép kiszámítható | |
| A legbővebb jelölés, ami az összes résztvevő halmazt és az elemenkénti hozzárendelést függvényszimbolikával és képlettel adja meg, ahol a képlet a kép kiszámításának módját adja meg. | |
| Szürjektív függvény (Szürjekció) -ból -be | |
| Injektív függvény (Injekció) -ból -be | |
|
Az jelölést relációkra is használják. |
Bijektív függvény (Bijekció) -ból -be |
| Beágyazás, inklúzió, természetes inklúzió, természetes beágyazása -be ( részhalmaza -nek, és a függvény minden elemét önmagára képezi.) | |
|
|
Identitásfüggvény, identitás, identikus leképezése A-nak vagy identikus leképezése -be ( és a függvény minden elemhez önmagát rendeli.) |
|
|
Izomorfizmus -ból -be |
| Parciális függvény -ból -be | |
| Többértékű függvény, multifüggvény | |
(illetve …) |
Az -ból -be menő függvények, illetve parciális függvények halmaza (kontextus, illetve a szerző szóhasználata alapján) |
Ezek a szimbólumok értelemszerűen kombinálhatók egymással.
Kapcsolódó szócikkek[szerkesztés]
További információk[szerkesztés]
Érdekes grafikonú függvények a Wolfram World-ön:
Források[szerkesztés]
- Rédei László: Algebra I. kötet, Akadémiai Kiadó, Bp (1954)
- Szendrei Ágnes: Diszkrét matematika, Polygon, JATE Bolyai Intézet, Szeged (1994)
- Balázs Márton, Kolumbán József: Matematikai analízis, Dacia Könyvkiadó, Kolozsvár-Napoca (1978)
- Heinz-Dieter Ebbinghaus: Einführung in die Mengenlehre. 4. Auflage. Spektrum, Akademischer Verlag, Heidelberg u. a. 2003, ISBN 3-8274-1411-3.
- Paul R. Halmos: Naive Mengenlehre (= Moderne Mathematik in elementarer Darstellung. Bd. 6). Übersetzt von Manfred Armbrust und Fritz Ostermann. 5. Auflage. Vandenhoeck & Ruprecht, Göttingen 1994, ISBN 3-525-40527-8.
- Arnold Oberschelp: Allgemeine Mengenlehre. BI-Wissenschafts-Verlag, Mannheim u. a. 1994, ISBN 3-411-17271-1.
- Adolf P. Youschkevitch: The Concept of Function up to the Middle of the 19th Century. In: Archive of the History of Exakt Sciences. 16 Springer Verlag, Berlin 1976.
- Mathworld
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Funktion (Mathematik) című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek[szerkesztés]
- ↑ Csörnyei Zoltán. Lambda-kalkulus. Typotex Kiadó (2007)
- ↑ a b H. König. Entwurf und Strukturtheorie von Steuerungen für Fertigungseinrichtungen. Berlin / Heidelberg: Springer-Verlag, 15–17. o. (1976) Hier: Seite 21f
- ↑ Nicolas Bourbaki: Éléments de mathématiques. Théorie des Ensembles. II.
























































![{\displaystyle Z^{D},\ {}^{D}Z,\ [D\to Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8a3efbec5b42fa81ba2142e9a623bc670681851)







































![{\displaystyle [D\rightharpoonup Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad0c804a555ba1b55160981ae0e4384eaa84c3c1)
![{\displaystyle [D\rightharpoonup Z]=\bigcup \limits _{X\subseteq {D}}[X\to Z]=\bigcup \limits _{X\subseteq {D}}Z^{X}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49acf8342679017f23cf89d4e5e218788a8d7154)
![{\displaystyle \left|[D\rightharpoonup Z]\right|=(|Z|+1)^{|D|}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e63327c2efce22d696c88445af6e9d7183f615c0)
































![{\displaystyle [A\to B]=B^{A}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd84487e3ecce4319bfbc282ef2adb22713f616a)
![{\displaystyle [A\rightharpoonup B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cf08908d7847e96631a3b47862b405584be38fb)