Átmenetiállapot-elmélet
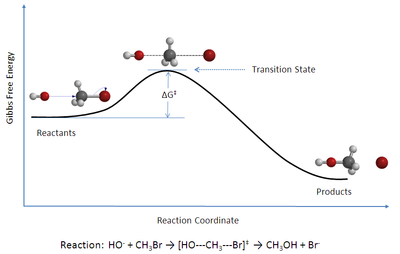
Az átmenetiállapot-elmélet (más néven aktivált komplex elmélet, abszolút sebességi elmélet[1] vagy átmeneti komplex elmélet[2]) az elemi reakciók sebességének magyarázatára alkotott elmélet, mely feltételezi, hogy a reakció kiindulási anyagai és az átmeneti állapot aktivált komplexei között sajátos kémiai egyensúly (kvázi-egyensúly) létezik.[3]
Az átmenetiállapot-elméletet elsősorban arra használják, hogy minőségileg megértsék, hogyan megy végbe egy kémiai reakció. Eredeti célkitűzésével szemben az átmenetiállapot-elmélet kevésbé bizonyult sikeresnek a reakciósebességi állandók abszolút értékének számolására, mivel ahhoz a potenciális energia felületek pontos ismeretére lenne szükség,[4] de segítségével kiszámítható egy adott reakció standard aktiválási entalpiája (Δ‡H⦵), standard aktiválási entrópiája (Δ‡S⦵) és az aktiválás standard szabadentalpiája (Δ‡G⦵), ha kísérletileg ismert a reakció sebességi állandója. (A ‡ jelölés az adott mennyiség átmeneti állapotban vett értékét jelöli.)
Az elméletet 1935-ben párhuzamosan dolgozta ki az akkoriban a Princetoni Egyetemen dolgozó Henry Eyring, valamint a Manchesteri Egyetem két kutatója, Meredith Gwynne Evans és Polányi Mihály.[5][6] Az átmenetiállapot-elmélet kidolgozása előtt a reakciók energiagátjának meghatározására széles körben használták az Arrhenius-féle sebességi törvényt. Az Arrhenius-egyenlet a tapasztalati megfigyelésekre épül, és figyelmen kívül hagyja a mechanisztikus megfontolásokat, mint például hogy egy reaktáns termékké alakulása során egy vagy több reaktív köztitermék szerepel-e.[7] Emiatt további fejlődésre volt szükség, hogy az ebben a törvényben szereplő két paraméter, a(z A) preexponenciális tényező és az (Ea) aktiválási energia jelentését megértsék. Az átmenetiállapot-elmélet, mely az Eyring-egyenlet felírásához vezetett, sikeresen megoldja ezt a két kérdést, ám az Arrhenius-egyenlet (1889) és az átmenetiállapot-elméletből levezetett Eyring-egyenlet (1935) publikálása között 46 év telt el. Ezen időszak alatt számos kutató és tudós járult jelentős mértékben hozzá az elmélet kifejlesztéséhez.
Elmélet[szerkesztés]
Az átmenetiállapot-elmélet alapötletei a következők:
- A reakciók sebességét a potenciális energia felület nyeregpontjában található aktivált komplexek vizsgálatával tanulmányozzák. A komplex kialakulási módjának nincs jelentősége.
- az aktivált komplexek sajátos egyensúlyban (kvázi-egyensúlyban) vannak a reaktáns molekulákkal.
- Az aktivált komplexek átalakulhatnak termékekké, ennek sebességét a kinetikus elmélettel ki lehet számítani.
Az elmélet kialakulása[szerkesztés]
Az aktivált komplex elmélet kialakulása során három megközelítést alkalmaztak, ezeket alább összefoglaljuk.
Termodinamikai tárgyalás[szerkesztés]
1884-ben Jacobus van ’t Hoff a megfordítható reakciók egyensúlyi állandójának hőmérsékletfüggésére felírta a Van ’t Hoff-egyenletet:
melyben ΔU a belső energia változása, K a reakció egyensúlyi állandója, R az egyetemes gázállandó, T pedig a termodinamikai hőmérséklet. Kísérleti munkák alapján Svante Arrhenius 1889-ben hasonló kifejezést állított fel a reakciók sebességi állandójának leírására:
Ennek a kifejezésnek az integrálásával az Arrhenius-egyenletet kapjuk:
A-t frekvencia tényezőnek nevezték (ma használt neve preexponenciális tényező), E pedig az aktiválási energia. A 20. század elejére az Arrhenius-egyenletet sokan elfogadták, de A és E fizikai értelmezése továbbra is homályos volt. Emiatt számos reakciókinetikus – abbéli igyekezetében, hogy megkíséreljen A és E, valamint a kémiai reakcióért közvetlenül felelős molekuláris dinamika között kapcsolatot találni – alternatív elméletet dolgozott ki annak leírására, hogy hogyan történnek a kémiai reakciók.[forrás?]
1910-ben Rene Marcelin bevezette a standard aktiválási szabadentalpia fogalmát, ez az összefüggés az alábbi módon írható fel:
Marcalin munkásságával nagyjából egy időben három holland kémikus, Philip Abraham Kohnstamm, Frans Eppo Cornelis Scheffer és Wiedold Frans Brandsma bevezette a standard aktiválási entrópia és a standard aktiválási entalpia fogalmát. A sebességi állandók leírására az alábbi egyenletet javasolták:
Az állandók természete azonban továbbra is tisztázatlan marad.
A kinetikus elmélet szerinti tárgyalás[szerkesztés]
Az 1900-as évek elején Max Trautz és William Lewis a reakciók sebességét a kinetikus gázelméleten alapuló ütközési elmélet segítségével vizsgálta. Az ütközési elmélet a reagáló molekulákat egymással ütköző merev gömböknek tekinti. Ez az elmélet nem veszi figyelembe az entrópiaváltozásokat.
Lewis ezt a tárgyalásmódot az alábbi reakcióra alkalmazva a kísérleti eredményekkel jó egyezést kapott:
2HI → H2 + I2
Később azonban, amikor más reakciókat hasonlóan akartak leírni, nagy eltérések adódtak az elméletileg várt és a kísérletileg kapott értékek között.
Statisztikus mechanikai tárgyalás[szerkesztés]
A statisztikus mechanika fontos szerepet játszott az átmenetiállapot-elmélet fejlődésében, bár alkalmazása nagyon lassan történt meg ahhoz képest, hogy a 19. század közepén James Clerk Maxwell, Ludwig Boltzmann és Leopold Pfaundler számos közleményt publikált, melyekben az egyensúlyi állandót és a reakciósebességet a molekuláris mozgások és a molekulasebességek statisztikus eloszlása szempontjából tárgyalták.
Egészen 1912-ig kellett várni arra, hogy A. Berthoud francia kémikus a Maxwell–Boltzmann-eloszlás felhasználásával írja le a reakciósebességi állandót.
ahiol a és b az energiatagokhoz kapcsolódó állandók.
Két évvel később Marcelin alapvető hozzájárulást tett azáltal, hogy a kémiai reakciót egy pont fázistéren keresztül történő mozgásának tekintette. Ezután Gibbs statisztikus mechanikai eljárásait követve hasonló kifejezést kapott, mint amilyet korábban termodinamikai megfontolások alapján vezetett le.
1915-ben újabb fontos eredményt ért el James Rice brit fizikus. Statisztikai elemzése alapján arra a következtetésre jutott, hogy a sebességi állandó arányos a „kritikus növekménnyel”. Elképzelését Tolman fejlesztette tovább. 1919-ben Karl Ferdinand Herzfeld osztrák fizikus a statisztikus mechanikát használta az egyensúlyi állandó vizsgálatára, és a fordított irányú reakció k-1 sebességi állandójának kinetikus elmélet szerinti leírását a fordított irányú, a kétatomos molekula disszociációját eredményező reakcióra.
Az előre irányú reakció sebességi állandójára a következő egyenletet kapta:
ahol a disszociációs energia az abszolút nulla hőmérsékleten, kB a Boltzmann-állandó, h a Planck-állandó, T a termodinamikai hőmérséklet, υ a kötés rezgési frekvenciája. Ez a kifejezés nagyon fontos, mivel a kBT/h kifejezés – mely az átmenetiállapot-elmélet kritikus eleme – ekkor jelent meg elsőként egy sebességi egyenletben.
1920-ban Richard Chase Tolman amerikai kémikus továbbfejlesztette Rice ötletét a kritikus növekményről.. Arra a következtetésre jutott, hogy egy reakció kritikus növekménye (mai nevén aktiválási energiája) egyenlő az összes, reakcióba lépő molekula átlagos energiájával, levonva abból az összes reaktáns molekula átlagos energiáját.
Potenciális energia felületek[szerkesztés]
A potenciális energia felület fogalma nagyon fontos volt az átmenetiállapot-elmélet kifejlesztése szempontjából. Ennek a fogalomnak az alapjait Marcelin rakta le. Ő úgy vélte, hogy a kémiai reakció végbemenetele leírható úgy, mint egy pont atomi impulzus és távolság koordinátákkal jellemzett haladása egy potenciális energia felületen.
1931-ben Eyring és Polányi Mihály megalkotta az alábbi reakció potenciális energia felületét. Ez a felület egy háromdimenziós ábra, mely kvantummechanikai elveken, valamint rezgési frekvenciák és disszociációs energiák kísérleti adatain alapul
H + H2 → H2 + H
Egy évvel Eyring és Polányi munkáját követően H. Pelzer és Wigner Jenő fontos hozzájárulást tett azáltal, hogy egy potenciális energia felületen követték egy reakció lezajlását. Ennek a munkának a jelentőségét az adta, hogy a potenciális energia felületeknél elsőként itt tárgyalták a nyeregpont fogalmát, és megállapították, hogy a reakció sebességét a rendszernek a nyeregponton való áthaladása határozza meg.
Az Eyring-egyenlet levezetése[szerkesztés]
Az Eyring, Polányi és Evans által hozzáadott egyetlen fontos újítás annak észrevétele volt, hogy az aktivált komplex kvázi-egyensúlyban van a reaktánsokkal. A sebesség így egyenesen arányos ezen komplexek koncentrációjának és azon (kBT/h) gyakoriságnak (frekvenciának) szorzatával, hogy az aktivált komplex milyen gyakran alakul át termékké.
Kvázi-egyensúlyi közelítés[8]
Megjegyzendő, hogy a kvázi-egyensúly különbözik a klasszikus kémiai egyensúlytól, de leírható ugyanazzal a termodinamikai formalizmussal. Vegyük az alábbi reakciót:
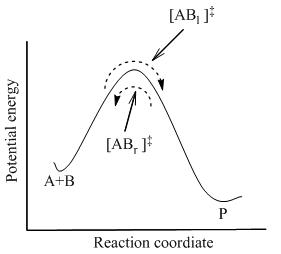
ahol teljesen beállt az egyensúly a rendszer minden komponense között, az [AB]‡ aktivált komplexet is beleértve. A statisztikus mechanika szerint [AB]‡ koncentrációja kiszámítható A és B koncentrációja függvényében.
Az átmenetiállapot-elmélet feltételezi, hogy még ha a reaktánsok és a termékek nincsenek is egyensúlyban egymással, az aktivált komplex kvázi-egyensúlyban van a reaktánsokkal. Amint a 2. ábrán látható, bármely pillanatban lesz jelen néhány aktivált komplex, melyek korábban reaktáns molekulák voltak, ezek jelölése [ABl]‡ (mivel balról jobbra mozognak). A többi aktivált komplex közvetlenül ezt megelőzően termék molekula volt [ABr]‡. Mivel a rendszer teljesen egyensúlyban van, [ABl] ‡ és [ABr]‡ koncentrációja azonos, és így mindkét koncentráció az összes aktivált komplex koncentrációjának a fele:
- and
Ha a termékmolekulákat hirtelen eltávolítjuk a rendszerből, akkor a termékből ([ABr]‡ ) aktivált komplexszé történő visszaalakulás megszűnik, de a balról jobbra zajló reakció nem áll le. Ezért feltételezhető, hogy a balról jobbra zajló reakció sebességét nem érinti a termék eltávolítása, másképp fogalmazva a kétféle irányban zajló folyamat egymástól feltehetően független.
Az átmenetiállapot-elméletben fontos felismerni, hogy amikor azt mondjuk, hogy az aktivált komplexek egyensúlyban vannak a reaktánsokkal, akkor ez csak azokra az ([ABl] ‡) aktivált komplexekre vonatkozik, amelyek korábban reaktáns molekulák voltak.
A kvázi-egyensúly K‡⦵ egyensúlyi állandója így írható fel:
Vagyis az AB‡ átmeneti állapot koncentrációja
Így a termék keletkezésének sebességi egyenlete:
A k sebességi állandó:
k‡ egyenesen arányos az aktivált komplexből termékké történő átalakulást okozó rezgési mód frekvenciájával, ennek a frekvenciának jele ν. Nem minden rezgés vezet termék keletkezéséhez, ezt egy arányossági állandó, a κ transzmissziós tényező bevezetésével vesszük figyelembe. k‡ tehát így írható fel:
A K‡ egyensúlyi állandóra a statisztikus mechanika hőmérsékletfüggő kifejezést ad:
ahol
A k‡ és K‡ új kifejezéseit egyesítve a sebességi állandóra az alábbi kifejezést kapjuk:
Mivel ΔG = ΔH –TΔS, a sebességi állandó kifejezése bővíthető, így kapjuk az Eyring-egyenletet:
Kísérleti sebességi adatok felhasználásával az átmenetiállapot-elmélet sebességi állandójának kifejezéséből kiszámolható Δ‡G⦵, Δ‡H⦵, Δ‡S⦵ és akár Δ‡V (aktiválási térfogat) is.
Az átmenetiállapot-elmélet korlátai[szerkesztés]
Az elmélet a kutatók számára fogalmi alapot nyújtott ahhoz, hogy megértsék, hogyan zajlanak le a kémiai reakciók. Noha az elméletet széles körben elfogadják, vannak korlátai. Az elmélet például feltételezi, hogy miután az átmeneti szerkezet megindul lefelé a potenciális energia felületen, akkor egyféle termék (vagy termékek halmaza) keletkezik. A reakciók egy részében ugyanakkor az átmeneti állapot olyan utat járhat be a potenciális energia felületen, melynek révén váratlan termékszelektivitás lép fel, amit az átmenetiállapot-elmélet nem jósol meg (ilyen reakció például a diazabiciklopentaének hőbomlása, melyet Anslyn és Dougherty írt le).
Az átmenetiállapot-elmélet azt is feltételezi, hogy az atommagok a klasszikus mechanika szerint viselkednek.[9] Feltételezi, hogy a reakció nem megy végbe, hacsak az ütköző atomoknak vagy molekuláknak nincs elég energiájuk ahhoz, hogy kialakuljon az átmeneti szerkezet. A kvantummechanika szerint azonban bármilyen véges energiagát esetén van esélye annak, hogy a részecske az alagúteffektus révén leküzdje a gátat.[10] Noha ez a hatás a nagy aktiválási energiát igénylő reakciók esetén várhatóan elhanyagolható mértékű, a viszonylag kis aktiválási gáttal rendelkező reakciók esetén jelentősebb tényezővé válik, mivel az alagúthatás valószínűsége a gát magasságának csökkenésével megnő.
Az átmenetiállapot-elmélet néhány magas hőmérsékletű reakció esetén nem működik. Az elmélet feltételezi, hogy a reagáló rendszer a potenciális energia felület legalacsonyabb nyergén fog áthaladni. Ennek a nyeregnek a legmagasabb pontja az átmeneti állapot. Ez a leírás ellentmondásmentes a viszonylag alacsony hőmérsékleten végbemenő reakciók esetén, magasabb hőmérsékleten azonban a molekulák a magasabb rezgési állapotokat foglalják el, mozgásuk összetettebbé válik és az ütközések révén olyan átmeneti állapotok is létrejöhetnek, melyek jóval távolabb esnek az átmenetiállapot-elmélet alapján előre jelzettektől. Ez az átmenetiállapot-elmélettől való eltérés még az egyszerű kétatomos hidrogénmolekula és a hidrogéngyök közötti kicserélődési reakció esetén is megfigyelhető.[11]
Jegyzetek[szerkesztés]
- ↑ Keszei Ernő. 4. Az átmeneti állapot kísérleti tanulmányozása, Femtokémia
- ↑ Gáspár Vilmos és Bazsa György recenziója M.J. Pilling - P.W. Seakins: Reakciókinetika című könyvének magyar fordításáról. [2016. március 5-i dátummal az eredetiből archiválva]. (Hozzáférés: 2012. október 28.)
- ↑ International Union of Pure and Applied Chemistry (IUPAC). Transition State Theory. http://goldbook.iupac.org/T06470.html (accessed November 23, 2008)
- ↑ Truhlar, D. G.; Garrett, B. C.; Klippenstein, S. J., Current Status of Transition-State Theory. The Journal of physical chemistry 1996, 100, (31), 12771-12800
- ↑ Laidler, K.; King, C, Development of transition-state theory. The Journal of physical chemistry 1983, 87, (15), 2657
- ↑ Laidler, K.; King, C, A lifetime of transition-state theory. The chemical intelligencer 1998, 4, (3), 39
- ↑ Eric V. Anslyn and Dennis A. Dougherty. Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365-373
- ↑ Laidler, K. J., Theories of Chemical Reaction Rates (McGraw-Hill Series in Advanced Chemistry). 1969; p 234 pp
- ↑ Eyring, H.; Journal of Chemical Physics, 1935, 3, 107-115
- ↑ Masel, R. Principles of Adsorption and Reactions on Solid Surfaces; Wiley, New York, 1996
- ↑ Pineda, J. R.; Schwartz, S. D.; Philosophical Transactions of the Royal Society B 2006, 361, 1433-1438
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Transition state theory című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Források[szerkesztés]
- Laidler, K.; King, C., Development of transition-state theory. The Journal of physical chemistry 1983, 87, (15), 2657
- Laidler, K., A lifetime of transition-state theory. The chemical intelligencer 1998, 4, (3), 39
- Eric V. Anslyn, Dennis A. Doughtery., Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365–373
- Schramm, VL., Enzymatic Transition States and Transition State Analog Design. Annual Review of Biochemistry 1998, 67, 693-720
- Schramm, V.L., Enzymatic Transition State Theory and Transition State Analogue Design. Journal of Biological Chemistry 2007, 282, (39), 28297-28300
- Radzicka, A.; Woldenden, R., Transition State and Multisubstrate$Analog Inhibitors. Methods in Enzymology 1995, 249, 284-312
- Cleland, W.W., Isotope Effects: Determination of Enzyme Transition State Structure. Methods in Enzymology 1995, 249, 341-373










![{\displaystyle \mathrm {A} +\mathrm {B} \rightleftharpoons [\mathrm {AB} ]^{\ddagger }\to \mathrm {P} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6173f1d72ff092dc982c275f2b4cc3faf7934f97)
![{\displaystyle [AB_{\mathrm {r} }]^{\ddagger }={\frac {1}{2}}[AB]^{\ddagger }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/718aea8ee732afe4cab765c29977124ad36b5b9e)
![{\displaystyle [AB_{\mathrm {l} }]^{\ddagger }={\frac {1}{2}}[AB]^{\ddagger }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5fcb4730a299151b8e90fe11b0e7cd933b45dad)
![{\displaystyle K^{\ddagger \ominus }={\frac {[AB]^{\ddagger }}{[A][B]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b0d08053a799ac0a101205501c399240c53dab)
![{\displaystyle [\mathrm {AB} ]^{\ddagger }=K^{\ddagger \ominus }[\mathrm {A} ][\mathrm {B} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/675438f6f9190c4de1aaa0bc3f147b6c105c13db)
![{\displaystyle {\frac {d[P]}{dt}}=k^{\ddagger \ominus }[\mathrm {AB} ]^{\ddagger }=k^{\ddagger }K^{\ddagger }[A][B]=k[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b59cfe1307532faaffcccff0851fece2bf2f03be)





